【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.指数加权平均
指数加权平均在统计中也叫做指数加权移动平均。通过它可以计算局部的平均值,来描述数值的变化趋势。
接下来通过一个例子来了解指数加权平均。
假设我们现在有一年中每一天的温度数据,将其绘制为散点图如下:
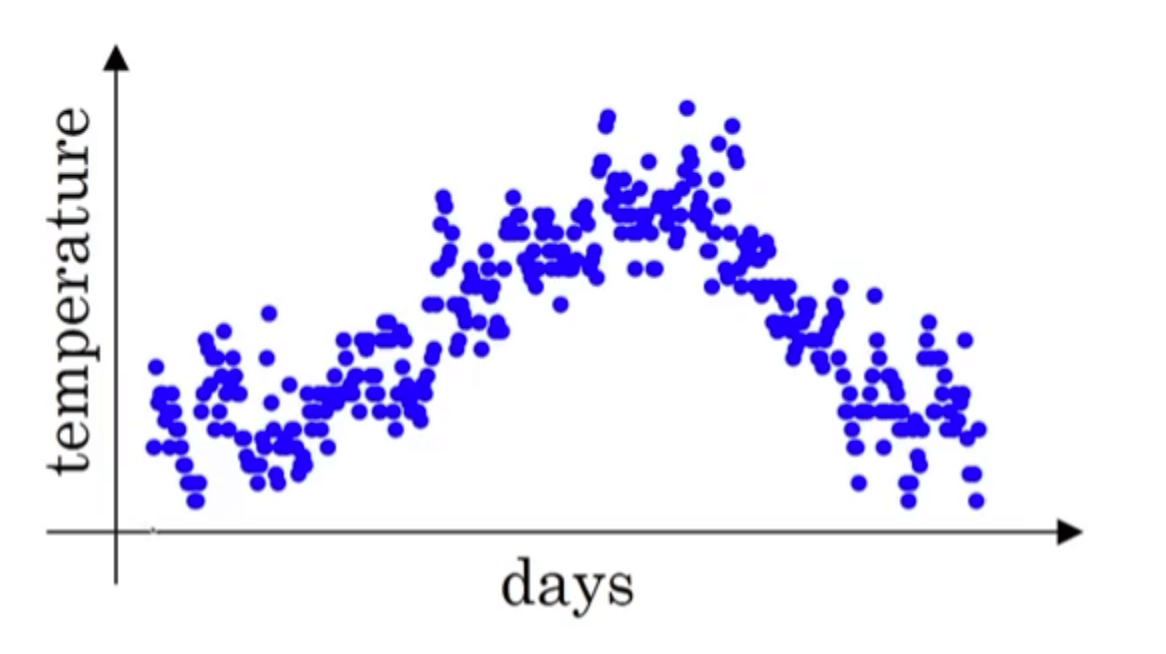
构造等式如下:
- $V_0=0$
- $V_1=0.9V_0+0.1\theta_1$
- $V_2=0.9V_1+0.1\theta_2$
- $V_3=0.9V_2+0.1\theta_3$
- ……
- $V_t=0.9V_{t-1}+0.1\theta_t$
其中,$\theta_t$表示第t天的温度。
然后依旧以天数作为横轴,求得的指数加权平均$V_t$作为纵坐标,得到如下红线:
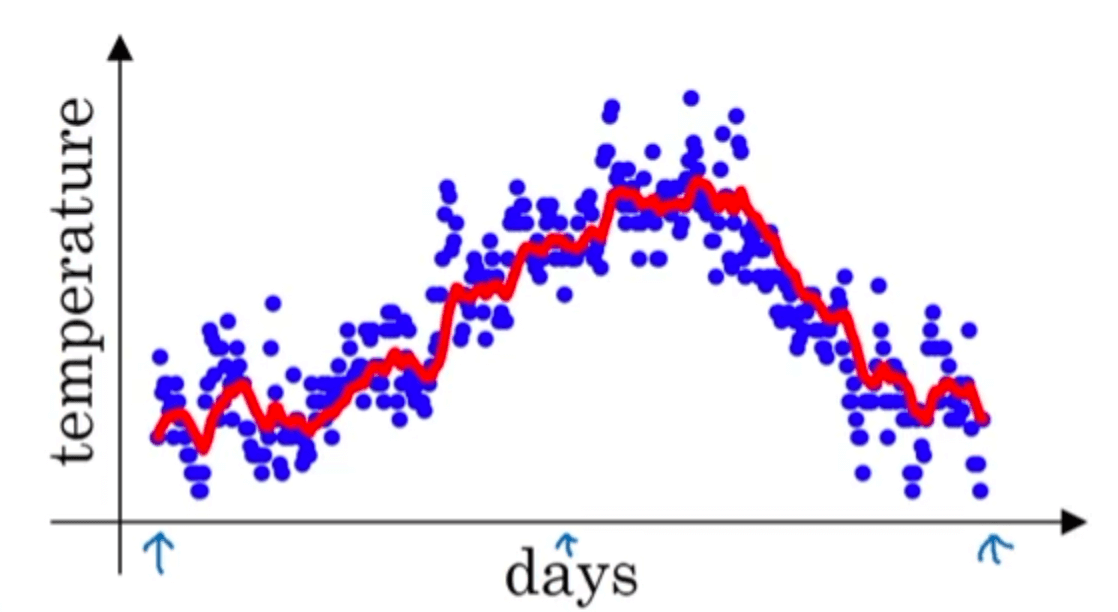
我们将上述公式写的更加泛化一点:
\[V_t=\beta V_{t-1}+(1-\beta) \theta_t\]在之前的例子中,$\beta=0.9$。其中$V_t$可近似理解为最近($\frac{1}{1-\beta}$)天的平均温度。
现在我们来考虑下$\beta$过大和过小时的情况。
👉如果有$\beta=0.98$,会得到下图的绿线:
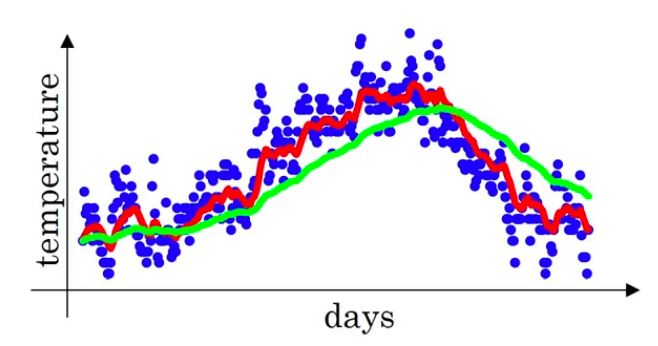
因为$\beta=0.98$相当于可近似为近($\frac{1}{1-0.98}=$)50天的平均温度,所以绿线要比红线更为平滑。
此外,因为当天温度的权值只有0.02,所以在温度变化时,绿线适应数据也更缓慢一些,会有一定延迟,因此绿线相比红线出现了右移的情况。
👉如果有$\beta=0.5$,会得到下图的黄线:
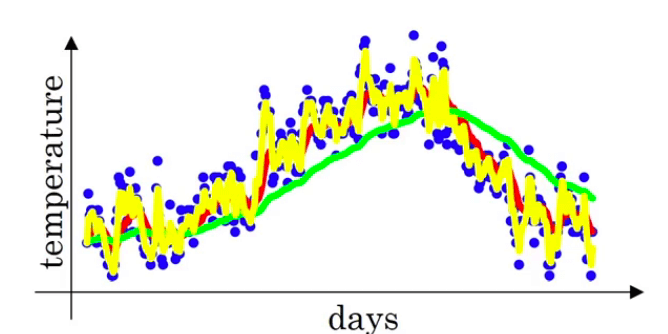
由于仅平均了两天的温度,所以得到的曲线有更多的噪声,更有可能出现异常值。但是这个曲线能够更快适应温度变化。
综上所述,选择一个不大不小的、合适的$\beta$能够更好的计算平均。
2.指数加权平均的作用
假设我们现在计算近100天温度的指数加权平均($\beta=0.9$):
- $V_{100}=0.9V_{99}+0.1\theta_{100}$
- $V_{99}=0.9V_{98}+0.1\theta_{99}$
- $V_{98}=0.9V_{97}+0.1\theta_{98}$
- $V_{97}=0.9V_{96}+0.1\theta_{97}$
- ……
带入可求得:
\[\begin{align} V_{100} & = 0.1\theta_{100} + 0.9V_{99} \\ & = 0.1\theta_{100} + 0.1*0.9\theta_{99} + 0.9^2V_{98} \\ & = 0.1\theta_{100}+0.1*0.9\theta_{99}+0.1*0.9^2\theta_{98}+0.9^3V_{97} \\ & = 0.1\theta_{100}+0.1*0.9\theta_{99}+0.1*0.9^2\theta_{98}+......+0.1*0.9^{99}\theta_1 \end{align}\]我们可以看到$V_{100}$是对过去一百天温度的指数加权平均。其权值呈指数衰减:

并且这些权值加起来等于1或接近于1。
但是距离越远的天数权值越小,计算时意义不大,因此通常省略权值小于$\frac{最大权值}{e}$的项。
本例中最大权值为0.1,则:
\[0.1*\frac{1}{e}\approx 0.1* 0.9^{10}\]即省略$\theta_{90}$之前的天数,所以对应于第1部分中提到的,$V_{100}$通常被近似为近($\frac{1}{1-0.9}=$)10天的加权平均温度。
同理,当$\beta=0.98$时,有$0.98^{50}\approx \frac{1}{e}$,此时,$V_{100}$被近似为近50天内的气温加权平均值。
根据极限的公式:$\lim_{x\to 0} (1-x)^{\frac{1}{x}}=\frac{1}{e}$,当$x=1-\beta$时,有$\beta^{\frac{1}{1-\beta}}\approx \frac{1}{e}$。因此我们就可以总结出指数加权平均可近似为近$\frac{1}{1-\beta}$天的平均温度。
2.1.指数加权平均的优势
相比使用算术平均计算局部平均值,指数加权平均不需要太多存储空间,只需在计算机内存中保留一行数字,并且基本一行代码即可实现,更为高效。虽然算数平均估计的均值更为准确,例如可以直接算出近十天或五十天的气温均值,但这样做的缺点是要保存所有的气温值及其气温值总和,需要更多的内存,更难实现,花费也更高。
因此,指数加权平均在机器学习中被广泛应用。
3.偏差修正
偏差修正会使得指数加权平均估计的更为准确。
在第1部分$\beta=0.98$时的例子中,绿线就是做完偏差修正之后的效果。如果没有偏差修正,得到的应该是下图中的紫线:

能注意到紫线的起点较低,但是后续趋势基本和绿线重合。
那为什么会出现这种情况呢?我们来分析一下。
假设第一天的温度是40华氏度,第二天的温度是55华氏度。假设$\beta=0.98$,则有:
- $V_0=0$
- $V_1=0.98V_0+0.02\theta_1=0.02\times 40=0.8$
- $V_2=0.98V_1+0.02\theta_2=0.98\times 0.8+0.02\times 55=1.884$
- ……
能看出前几天的估计有很大的偏差。因此我们需要对其进行修正:
\[\frac{V_t}{1-\beta^t}\]$V_1$修正之后的结果为($\frac{0.8}{1-0.98^1}=$)40;$V_2$修正之后的结果为($\frac{1.884}{1-0.98^2} \approx$)47.58。很明显,修正之后的结果更为准确。
并且随着t增加,$\beta^t$将接近于0,所以当t很大的时候,偏差修正几乎没有作用。这也就是当t很大的时候,紫线基本和绿线重合的原因。但是在初始阶段,偏差修正可以帮助我们更好的预测温度。当然也有部分人不注重初始阶段,因此也可以不使用偏差修正。