【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Momentum梯度下降法
Momentum梯度下降法的运行速度几乎总是快于标准的梯度下降法。
Momentum梯度下降法的基本思路就是计算梯度的指数加权平均数,并利用该梯度更新你的权重。
接下来我们来详细介绍下Momentum梯度下降法的计算过程。
假设cost function的图像见下:

其中红点代表最小值的位置。
标准的梯度下降法的过程见下:

这种上下波动减慢了梯度下降法的速度,使我们无法使用更大的学习率。
而对于Momentum梯度下降法,我们使用指数加权平均综合前几次迭代的梯度:
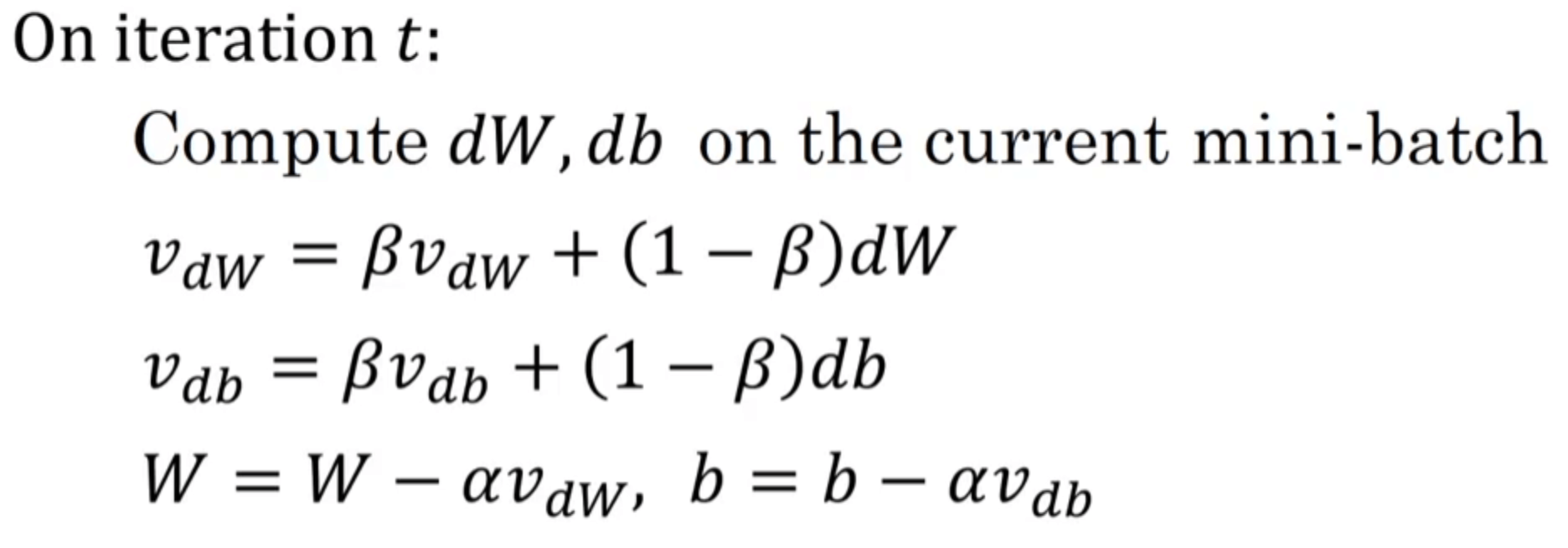
$v_{dW}$和$v_{db}$依旧是被初始化为0。
Momentum梯度下降法的过程如下图红线所示:

梯度的方向更为直接的指向了最小值,减少了上下摆动。
Momentum梯度下降法涉及两个超参数:学习率$\alpha$和参数$\beta$。其中,$\beta$最常用的值是0.9,即平均了前十次迭代的梯度。
此外,在使用Momentum梯度下降时,基本不进行偏差修正。因为通常迭代次数都大于10次(以$\beta=0.9$为例),指数加权平均已经过了初始阶段,因此不再需要偏差修正。
在部分资料中,有把指数加权平均公式中的$(1-\beta)$省去的写法,但此时$\beta$通常还是取0.9。