本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
本文通过构建一个回归模型来进一步熟悉tensorflow在实际中的应用。
2.准备训练数据
1
2
3
x_data=np.linspace(-0.5,0.5,200,axis=0).reshape(1,200)
noise=np.random.normal(0,0.02,x_data.shape)
y_data=np.square(x_data)+noise
numpy.linspace在指定的范围内返回均匀间隔的数字。例如,numpy.linspace(0,3,6)可在0到3的范围内均匀生成6个间隔相同的数字:0,0.6,1.2,1.8,2.4,3。因此在上述代码中,我们生成了范围在-0.5到0.5的200个数字作为我们的训练数据。
然后我们通过正态分布产生一些噪声,$x^2$加上噪声作为我们训练数据的标签。
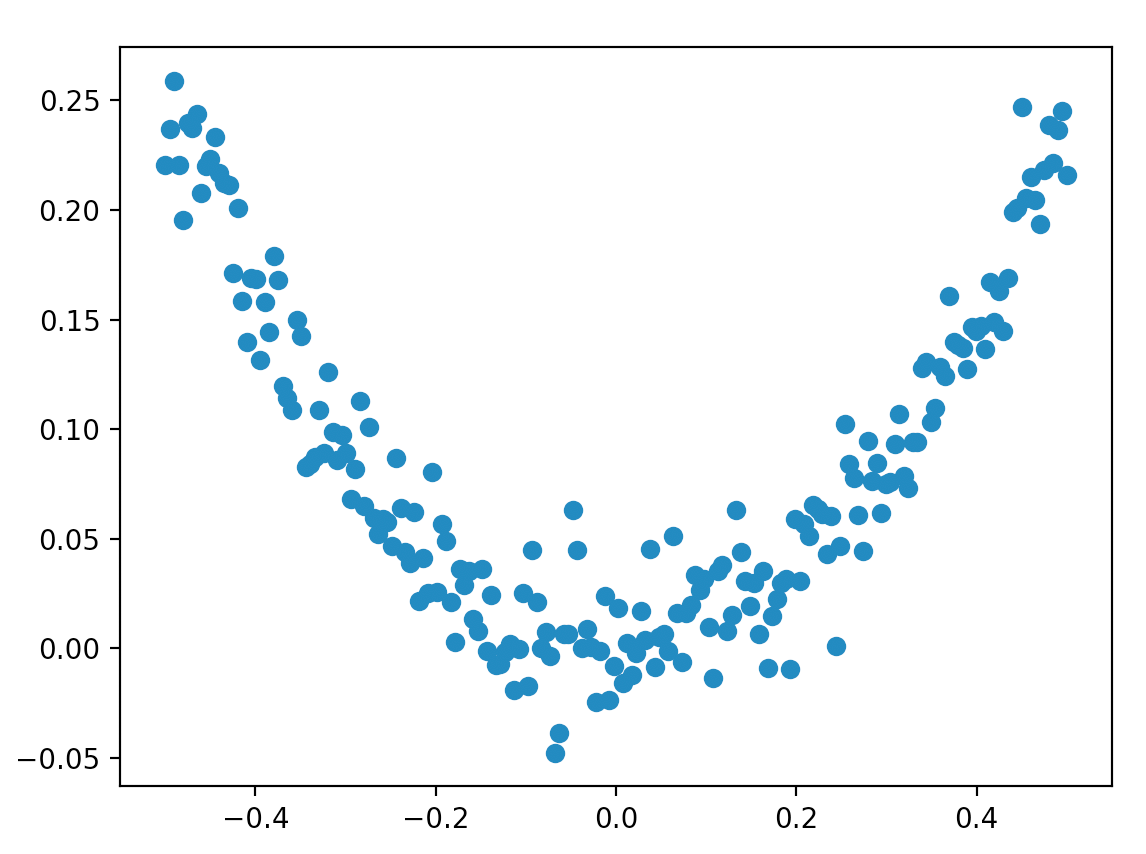
最终生成的训练数据分布见下图:
使用numpy生成随机数的几种方式:
numpy.random.rand(d0,d1,...,dn)生成的随机数位于[0,1)之间。参数为生成的随机数的维度。
numpy.random.randn(d0,d1,...,dn)生成的随机数来自标准正态分布。参数为生成的随机数的维度。
numpy.random.normal(loc,scale,size)生成的随机数来自正态分布。正态分布的$\mu$和$\sigma$由参数loc和scale传入。
3.定义神经网络
3.1.网络的输入、输出
我们通过placeholder定义网络的输入和输出:
1
2
x=tf.placeholder(tf.float32,[1,None])
y=tf.placeholder(tf.float32,[1,None])
[1,None]表示我们的数据只有1行,并且列数不确定,即样本个数不确定。
3.2.网络的隐藏层
这里我们使用一个双层神经网络,即只含有一个隐藏层。并且假设该隐藏层有10个神经元。激活函数统一使用tanh函数。
1
2
3
4
W_L1=tf.Variable(tf.random_normal([10,1]))
b_L1=tf.Variable(tf.zeros([10,1]))
Z_L1=tf.matmul(W_L1,x)+b_L1
A_L1=tf.nn.tanh(Z_L1)
很简单直白的过程,不再赘述。
tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)用于生成来自正态分布的随机数,参数说明见下:
shape:输出的张量形状。mean:正态分布的均值,默认为0。stddev:正态分布的标准差,默认是1.0。dtype:输出的类型,默认是tf.float32。seed:随机数种子,是一个整数,当设置之后,每次生成的随机数都一样。name:操作的名称。
如果对这部分内容不熟悉,可先补一下有关深度学习的知识,可参考本人【深度学习基础】系列博客。
3.3.网络的输出层
1
2
3
4
W_L2=tf.Variable(tf.random_normal([1,10]))
b_L2=tf.Variable(tf.zeros(1,1))
Z_L2=tf.matmul(W_L2,A_L1)+b_L2
prediction=tf.nn.tanh(Z_L2)
4.cost function
使用均方误差计算cost function:
1
loss=tf.reduce_mean(tf.square(y-prediction))
tf.reduce_mean函数用于计算张量tensor沿着指定的数轴(tensor的某一维度)上的平均值,主要用作降维或者计算tensor的平均值。
tf.reduce_mean如果不指定轴(axis),则计算所有元素的均值。
5.优化方法
优化cost function的方法依旧采用梯度下降法:
1
train=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
这里将学习率设为0.1。
6.运行网络
一切准备就绪,就可以运行网络了。设置迭代次数为2000次:
1
2
for _ in range(2000):
sess.run(train,feed_dict={x:x_data,y:y_data})
⚠️记得通过feed操作喂入训练数据以及其标签。
最后拟合出来的模型见下图红线所示:
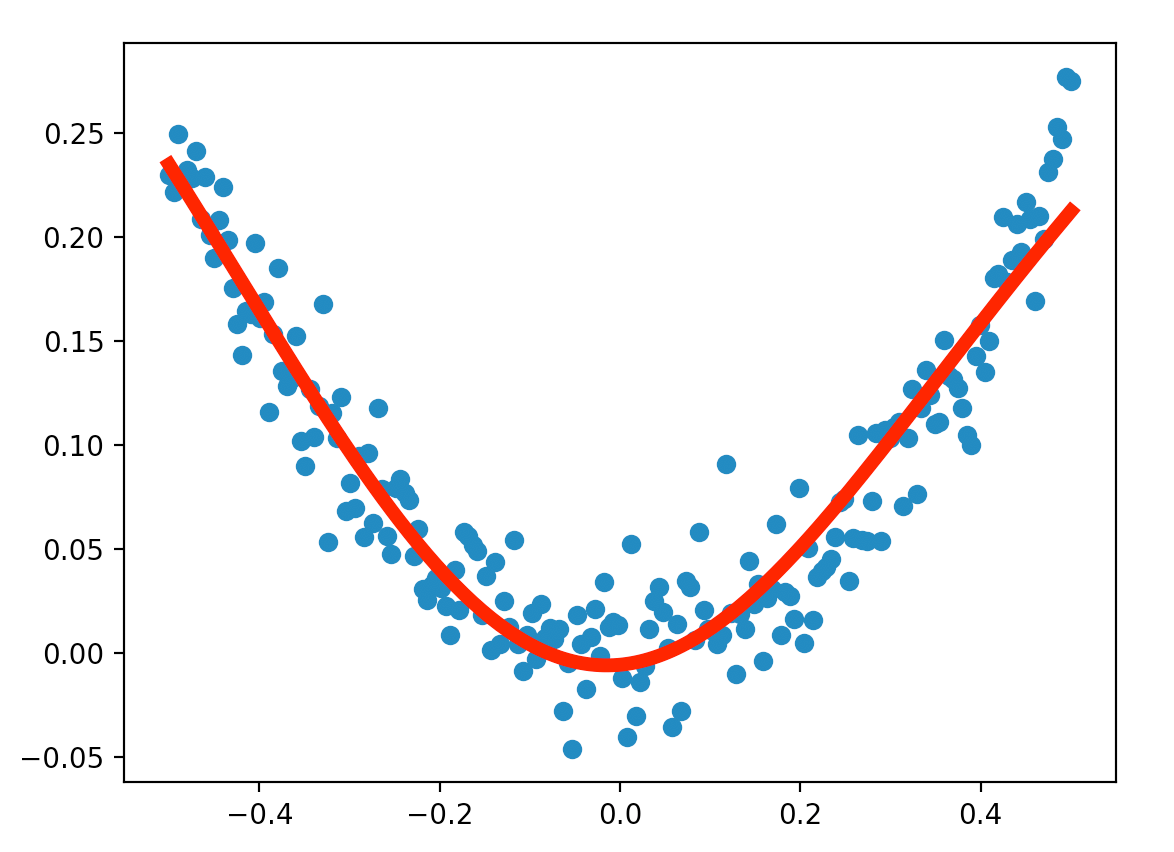
结果很不错。