【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.局部最优问题
人们总是担心优化算法会被困在局部最优。
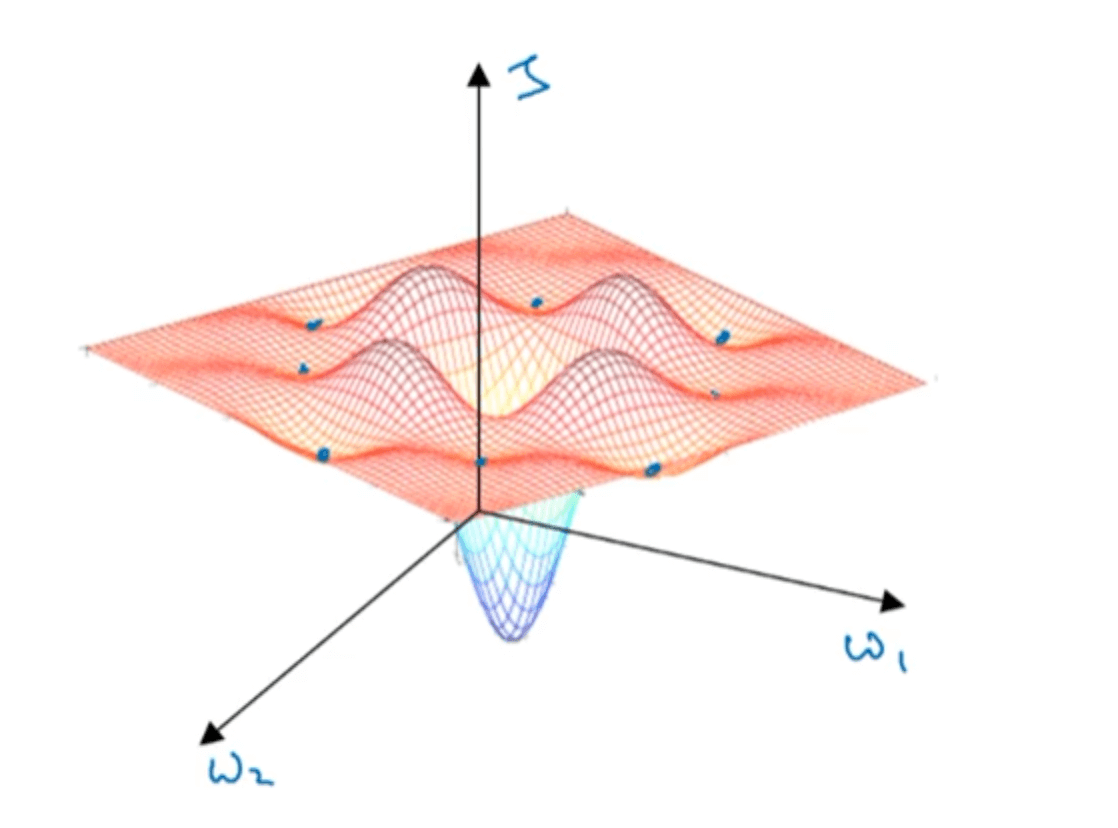
人们通常认为cost function的图像会像上图一样,存在很多局部最优点。而优化算法会被困在其中一个局部最优点,而无法达到全局最优点。
但实际情况是,上述现象只在参数很少的时候容易出现,比如只有两个参数$w_1,w_2$。当我们有很多参数时,在梯度为0且每个方向都是凸函数的点(即局部最优点)是很难出现的。更多的是当梯度为0时,有的方向是凸函数,有的方向是凹函数,即鞍点。
因此,当我们在训练较大的神经网络,存在大量参数,并且cost function被定义在较高的维度空间时,优化算法不太可能困在局部最优中。
2.Problem of plateaus
其实我们需要关注的问题在于平稳段。平稳段指的是导数长时间接近于0的一段区域,这会减慢学习效率。如下图所示:

这个时候,我们就需要之前博客中介绍的Momentum、RMSprop、Adam等加速学习算法。