【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
通过前面的学习,我们了解到了深度学习中会涉及到很多超参数,那么该如何确定这些超参数的值呢?本文就来简单的探讨一下这个问题。
2.超参数的重要性排序
在开始调试超参数之前,我们需要知道哪些超参数是需要优先被调整的,而哪些超参数是没有必要进行调整的。
不同超参数的调整对结果的影响程度是不同的。我们应该优先调整对模型影响较大的超参数。例如(按照超参数的重要性降序排列):
- 学习率$\alpha$。
- momentum梯度下降法中的$\beta$、mini-batch size、隐藏层的神经元数等。
- 神经网络的层数、学习率衰减中涉及的超参数等。
- adam优化算法中的$\beta_1,\beta_2,\epsilon$等。
3.随机取值
在早一代的机器学习算法中,超参数的调试常见做法是在网格中均匀的取点。假设现在需要调试两个超参数,我们使用$5\times 5$的网格:
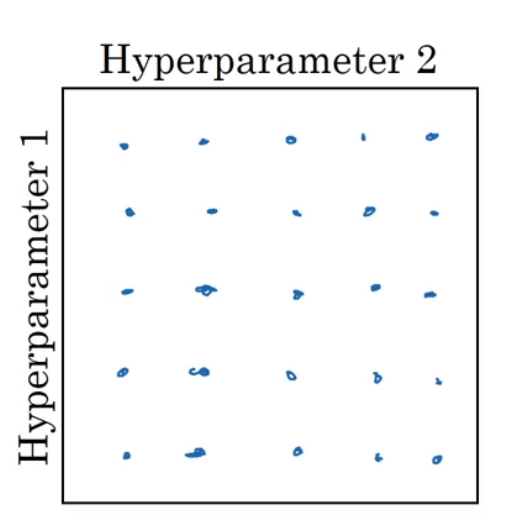
我们可以尝试这25个点,然后选择哪个参数效果最好。
但是这种方法有个弊端,举个例子说明一下。如果上图中超参数1是学习率,一个非常重要的超参数。超参数2是Adam算法中的$\epsilon$,一个非常不重要的超参数。此时,只有调整学习率是有意义的,虽然我们尝试了25个点,但是实际上只测试了5个不同的学习率。这样做明显效率很低。
鉴于此,我们将在网格中均匀取值改为随机取值(假设依然取25个点):
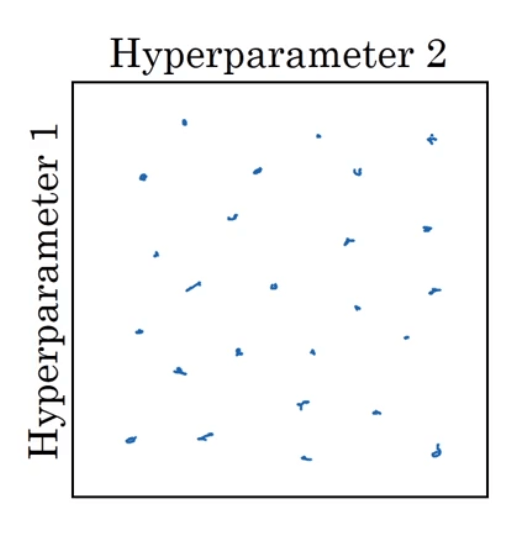
这样我们就相当于取到了25个不同的学习率,更容易发现效果最好的那个。
在实践中,我们搜索的超参数可能不止两个,因此搜索的空间可能是三维或者更高维度。
4.精细搜索
接着第3部分的例子,我们随机取了25个点。结果我们发现效果最好的几个点聚集在一个区域内。此时我们可以放大这块小区域,然后在其中更密集的取值:

这是一种从粗糙到精细的搜索策略。
5.随机取值的方法
随机取值和精细搜索可以提升我们搜索最优超参数的效率。那么我们现在回过头来说一下如何进行随机取值。
例如我们现在需要确定“神经网络层数”这个超参数,其取值范围为2~4。那么我们就可以进行线性随机取值,尝试2,3,4这几个值。又例如超参数“隐藏层的神经元数目”,假设其取值范围为50~100。那么我们就可以在50~100中进行随机取值即可。
但是并不是每个超参数都可以这样简单的直接随机取值。例如假设学习率的取值范围为0.0001~1,如果我们还按上述方法进行随机取值的话,那么有90%($\frac{1-0.1}{1-0.0001}=90\%$)的搜索资源会落在0.1~1之间,只有10%的搜索资源在0.0001~0.1之间,这显然是不合理的。这是因为取值范围跨越了多个数量级。因此我们可以先取对数:$10^{-4}=0.0001;10^0=1$,然后在[-4,0]这个范围内进行随机取值,使得学习率$\alpha=10^r,r\in [-4,0]$。
再举一个类似的例子,在计算指数加权平均时涉及的超参数$\beta$,假设其取值范围为0.9~0.999。根据之前讲的方法,我们可以搜索$1-\beta$的值(即范围为0.1~0.001),有$1-\beta=10^r,r\in [-3,-1]$。那么我们为什么不在0.9~0.999范围内线性随机取值呢?原因在于当$\beta$越接近于1,对结果的影响会越大。例如当$\beta=0.9$时,指数加权平均相当于平均了过去10($\frac{1}{1-0.9}$)组数据,当$\beta=0.9005$时,指数加权平均依旧相当于平均了过去10($\frac{1}{1-0.9005}$)组数据。但是当$\beta=0.999$时,指数加权平均相当于平均了过去1000($\frac{1}{1-0.999}$)组数据,当$\beta=0.9995$时,指数加权平均相当于平均了过去2000($\frac{1}{1-0.9995}$)组数据,这个差距明显要比之前大很多。因此此处依旧采用线性随机取值是不合理的。
不过在实际应用时,如果对每个超参数都采用了线性随机取值的方法时也不用担心,通过由粗糙到精细的搜索策略总能让你锁定更优的超参数。
6.超参数的搜索策略
6.1.Training many models in parallel
我们可以同时构建多个模型,分别尝试不同的超参数,根据其结果从而选出最优值。
6.2.Babysitting one model
如果因为CPU、GPU等机器性能的限制,无法同时尝试多组超参数。我们也可以只构建一个模型,然后随着训练的进行,根据cost function的下降趋势,不断的调整超参数的值,最终达到最优。