本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
我们以【Tensorflow基础】第四课:手写数字识别中构建的手写数字识别模型为例,对模型进行进一步的优化。
2.修改代价函数
在之前的模型中,我们用的是均方误差作为cost function。现在我们使用更合适的交叉熵损失函数作为cost function:
1
loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
结果对比见下:
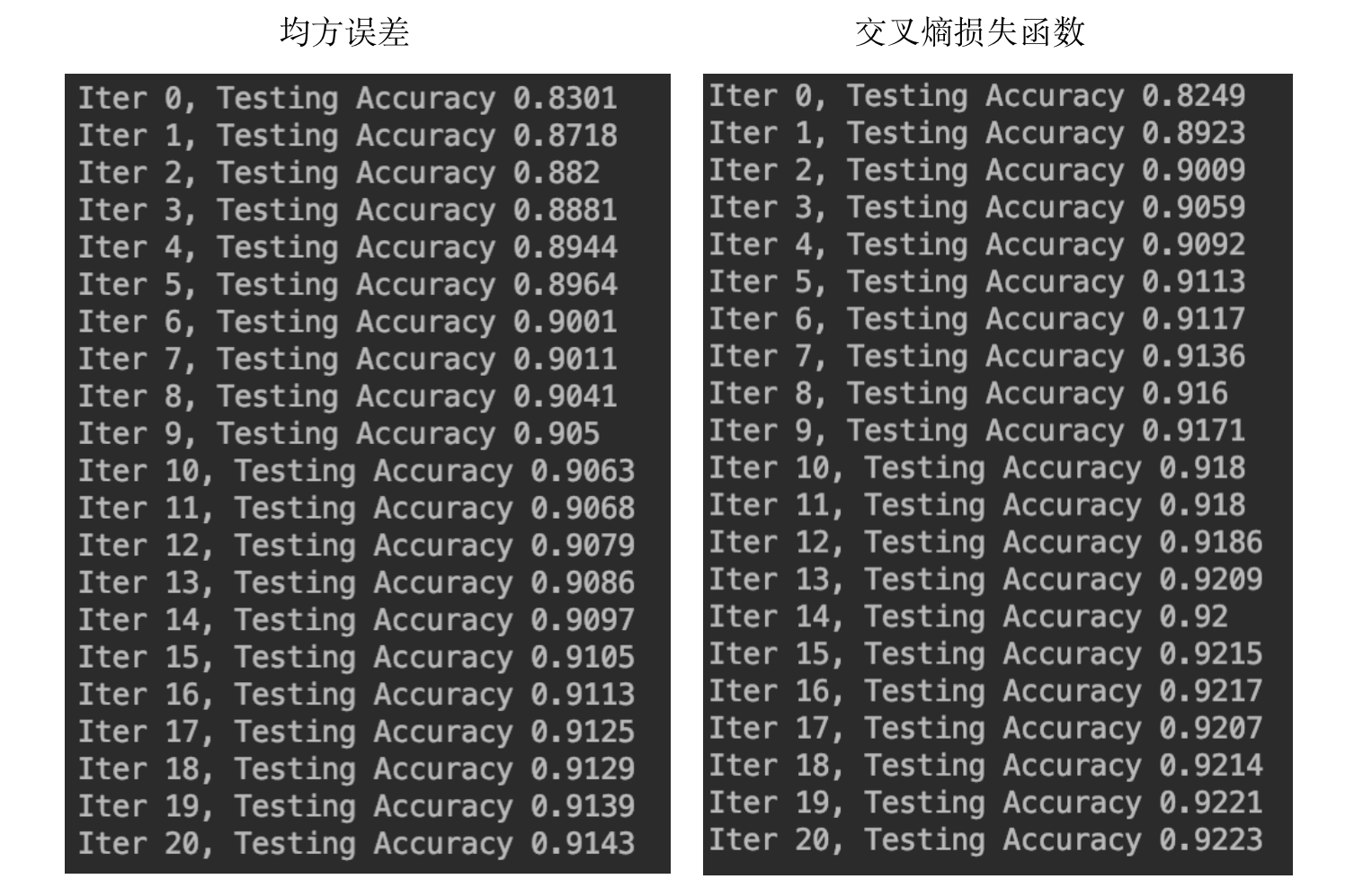
很明显,交叉熵损失函数效果更好,收敛速度更快。
在做tensor之间的加减乘除等基本运算时,也可以直接用
+-*\等符号,这些符号会被tensorflow自动重载为对应的接口函数,例如+被重载为tf.add()。
3.修改网络
在第2部分的基础上,对网络的结构和参数进行了如下修改:
- 添加隐藏层。
- 随机初始化权重。
- dropout防止过拟合。
为什么要随机初始化权重?请戳👉【深度学习基础】第十三课:梯度消失和梯度爆炸。
关于dropout的详细介绍,请戳👉【深度学习基础】第十一课:正则化。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#第一层
W1=tf.Variable(tf.truncated_normal([784,2000],stddev=0.1))
b1=tf.Variable(tf.zeros([2000])+0.1)
A1=tf.nn.tanh(tf.matmul(x,W1)+b1)
A1_drop=tf.nn.dropout(A1,keep_prob)
#第二层
W2=tf.Variable(tf.truncated_normal([2000,2000],stddev=0.1))
b2=tf.Variable(tf.zeros([2000])+0.1)
A2=tf.nn.tanh(tf.matmul(A1_drop,W2)+b2)
A2_drop=tf.nn.dropout(A2,keep_prob)
#第三层
W3=tf.Variable(tf.truncated_normal([2000,1000],stddev=0.1))
b3=tf.Variable(tf.zeros([1000])+0.1)
A3=tf.nn.tanh(tf.matmul(A2_drop,W3)+b3)
A3_drop=tf.nn.dropout(A3,keep_prob)
#输出层
W4=tf.Variable(tf.truncated_normal([1000,10],stddev=0.1))
b4=tf.Variable(tf.zeros([10])+0.1)
prediction=tf.nn.softmax(tf.matmul(A3_drop,W4)+b4)
函数tf.truncated_normal:
1
2
3
4
5
6
7
8
truncated_normal(
shape,#输出张量围度
mean=0.0,#均值
stddev=1.0,#标准差
dtype=dtypes.float32,#输出类型
seed=None,#随机数种子
name=None#运算名称
)
该函数可产生截断正态分布随机数,取值范围为$[mean-2\times stddev,mean+2\times stddev]$。
keep_prob在训练时设为0.7,预测时不能使用dropout,因此预测时keep_drop设为1.0。
修改后预测结果为:
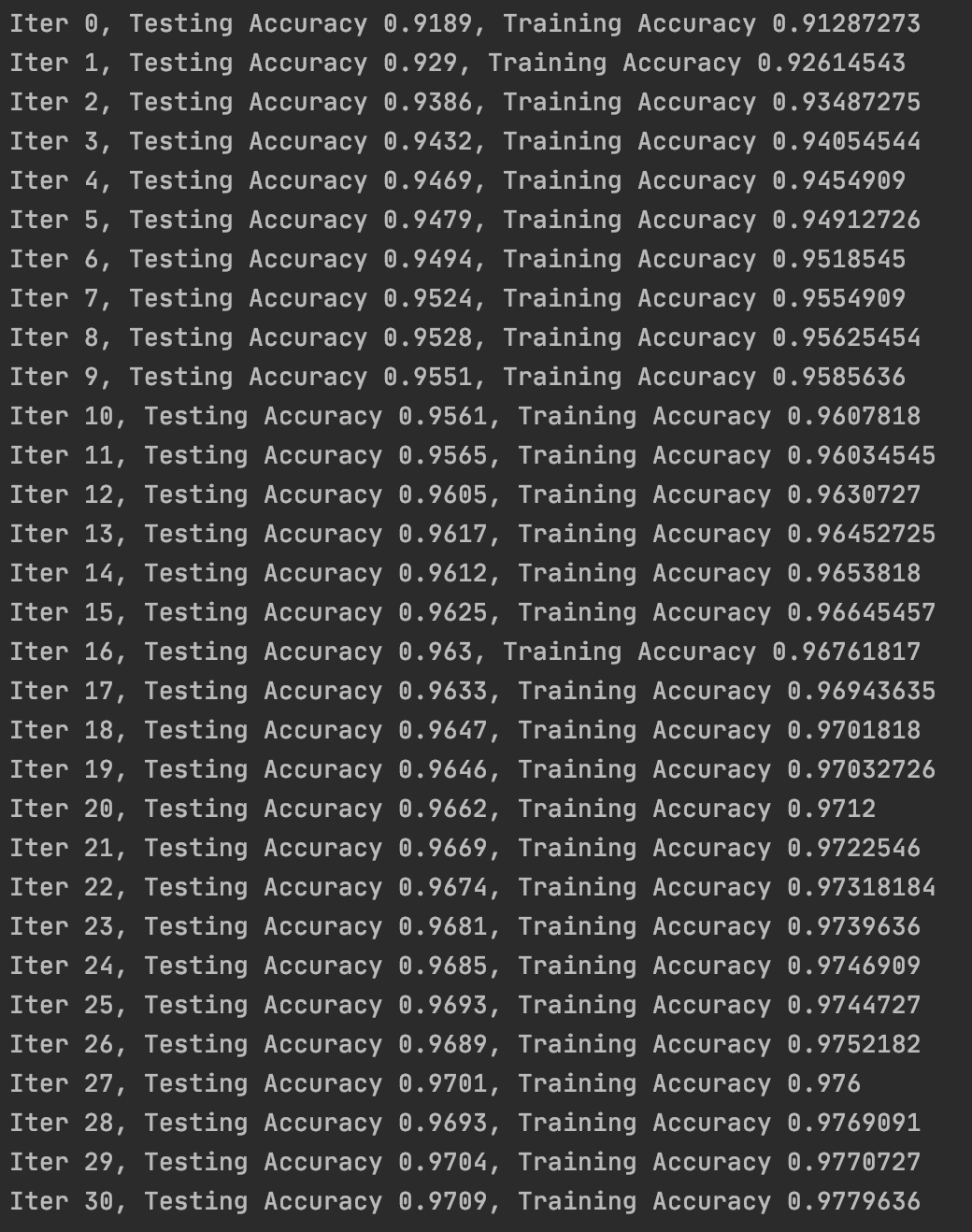
相比第2部分,结果又有了进一步的提升。
4.修改优化器
有很多优化算法可供选择:
- Adam优化算法:
tf.train.AdamOptimizer()。 - RMSProp优化算法:
tf.train.RMSPropOptimizer()。 - Momentum优化算法:
tf.train.MomentumOptimizer()。
例如我们选择Adam优化算法:
1
train_step=tf.train.AdamOptimizer(1e-2).minimize(loss)
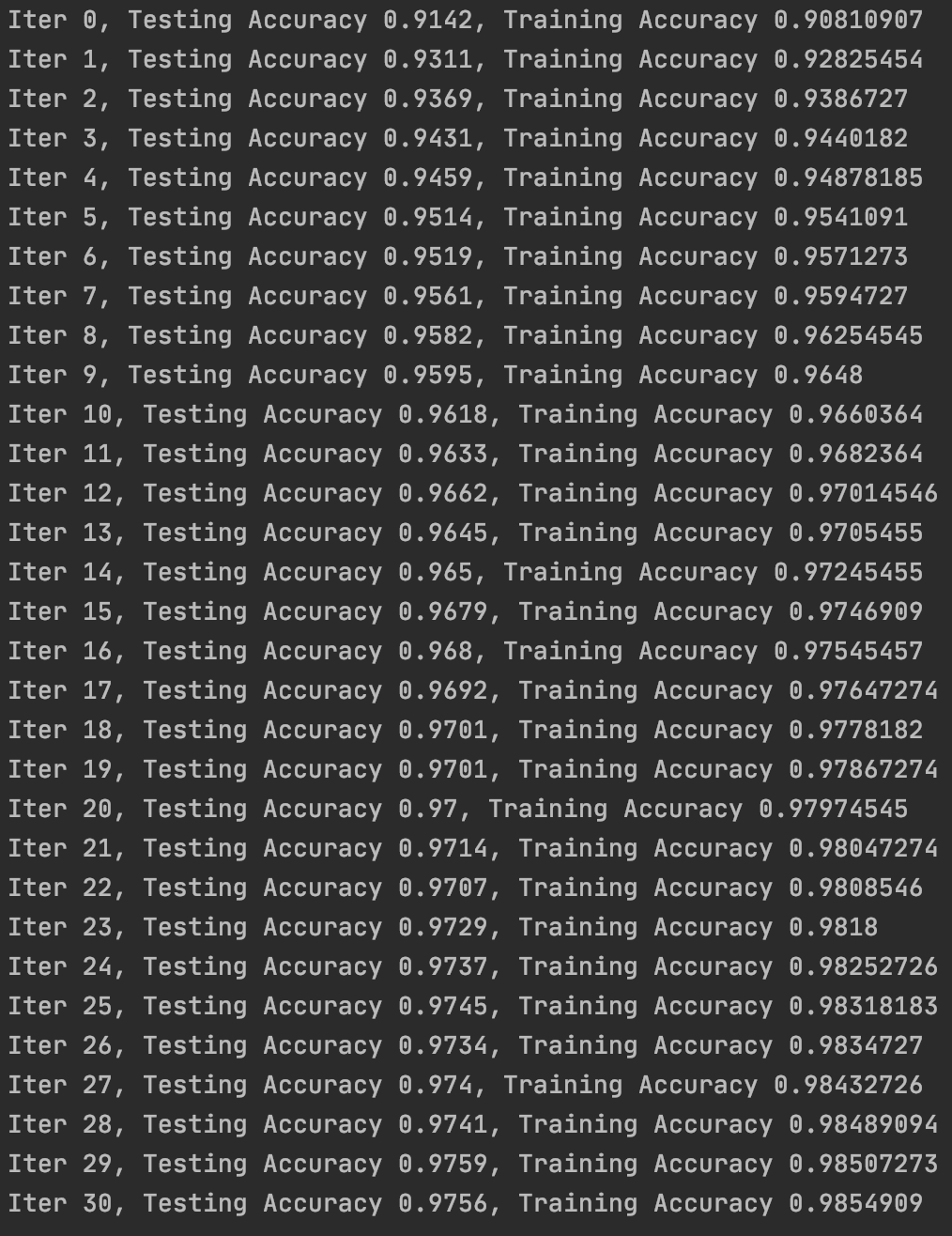
模型表现相比第3部分又有提升。
5.学习率衰减
详细讲解请见:【深度学习基础】第二十课:学习率衰减。
1
tf.assign(lr,0.001*(0.95**epoch))
执行之后模型的性能有了进一步的提升: