【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.bounding box的预测
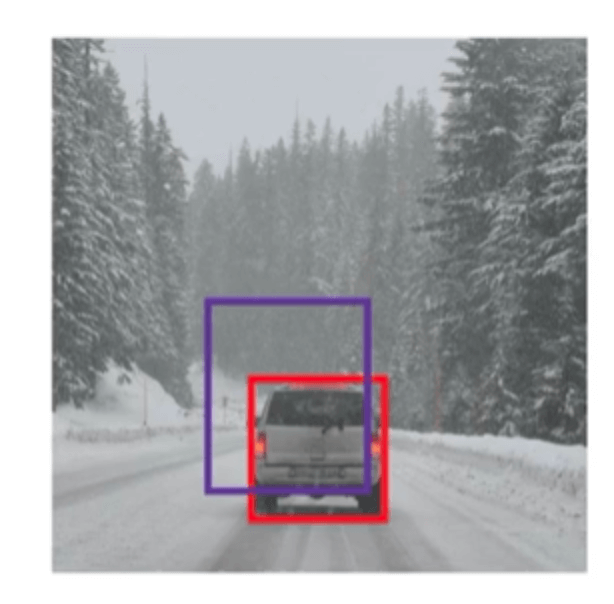
在上篇博客【深度学习基础】第三十三课:基于滑动窗口的目标检测算法中,我们介绍了基于滑动窗口的目标检测算法,但是该算法并不能输出最精准的bounding box。例如,我们尝试的滑动窗口没有一个能完美匹配目标位置,其最匹配窗口可能在下图蓝框所示位置:

而该汽车最优的bounding box则如上图中红框所示,并且不一定是矩形,可能是个梯形等形状。那么该如何确定一个准确的bounding box呢?方法之一就是使用YOLO算法。YOLO算法的全称是:You Only Look Once(YOLO算法确实也如名字的含义一样,运行速度非常快,可以达到实时检测)。接下来我们一起来看下YOLO算法是如何做的。
假设输入图像为$100\times 100 \times 3$,我们在图像上放置一个网格(grid),为了简化介绍,这里使用$3\times 3$的网格(实际应用时会使用更精细的网格,例如$19 \times 19$):
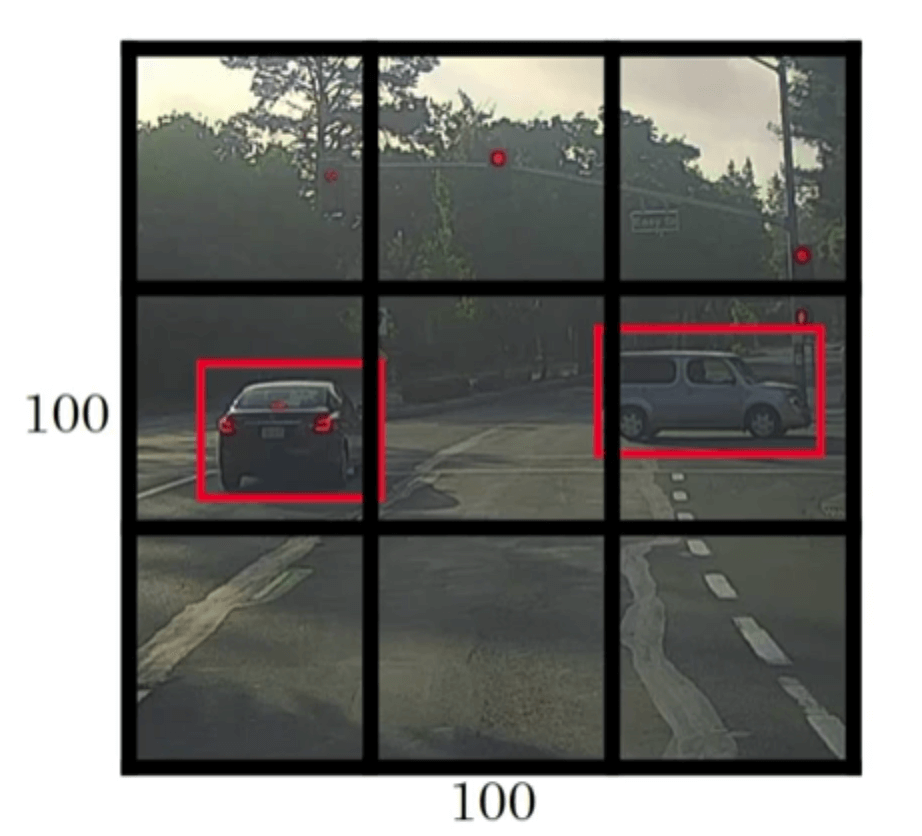
我们可以这样定义训练集的label,对于网格中的每一个格子(grid cell),都有(假设每一个格子最多只包含一个目标):
\[y=\begin{bmatrix} P_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \end{bmatrix}\]符号含义和【深度学习基础】第三十二课:目标定位和特征点检测中的相同,在此不再赘述。
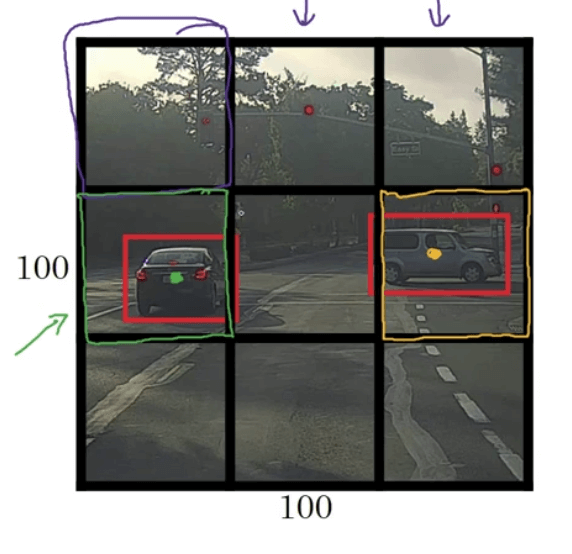
需要说明的是,目标归属于其中心点所在的格子。例如在下图中,第二行的第一和第三个格子各包含一个目标,而第二个格子则认为无目标存在,虽然第二个格子同时包含了两个目标的一部分:
每个格子我们都会得到一个8维向量的输出,因此总的输出维度为$3\times 3 \times 8$:
1.1.如何定义bounding box
本部分来说说在YOLO算法中如何定义bounding box,即$b_x,b_y,b_h,b_w$的值。
我们约定每一个格子左上角的坐标为$(0,0)$,右下角的坐标是$(1,1)$:
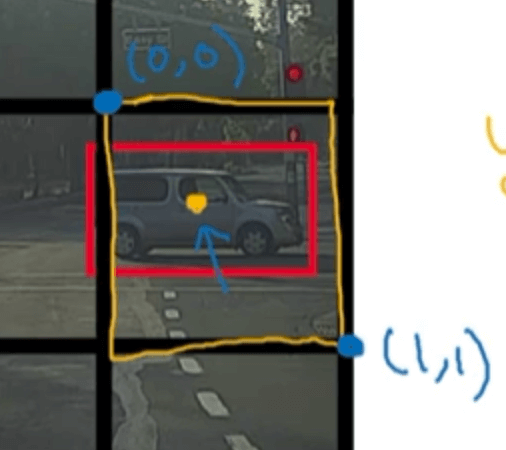
其中,$b_x,b_y$的范围在0到1内,而$b_h,b_w$则有可能大于1。例如在上图中,汽车的bounding box可标记为:$b_x=0.4,b_y=0.3,b_h=0.5,b_w=0.9$。
2.交并比
我们该如何判断目标检测算法结果的好坏呢?常用的一个评价指标就是交并比(Intersection over Union,简写为IoU)。
假设真实的bounding box如下图红框所示,而算法预测出来的bounding box如下图紫框所示:
IoU就是计算两个bounding box的交集和并集之比,即黄色区域面积比上绿色区域面积:

当$IoU\geqslant 0.5$时,通常认为预测结果就是正确的。当然也可以选取其他阈值,比如0.6、0.7等。IoU的值越高,预测的bounding box就越准确。
3.非极大值抑制
目标检测任务中存在的一个问题就是算法可能对同一个对象做出多次检测(即有多个格子都认为目标属于自己):
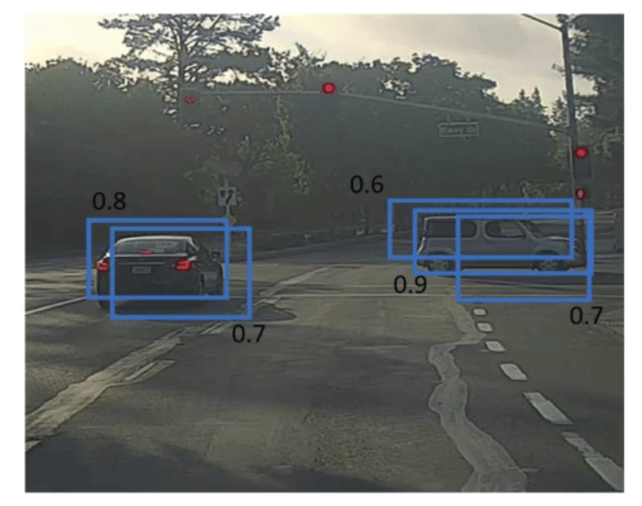
各个bounding box有着不同的预测概率。此时我们便可采用非极大值抑制(Non-Maximum Suppression,简写为NMS)来处理这些结果。
bounding box的概率可以通过$P_c \times c_n$来计算,$c_n$为该类别目标存在的概率。
我们先以上图中右侧的汽车为例,保留其最高概率的bounding box,删除与该bounding box有着较高IoU的其他bounding box。然后对左侧的汽车进行同样的处理。这样即可得到经过NMS后的最终结果:
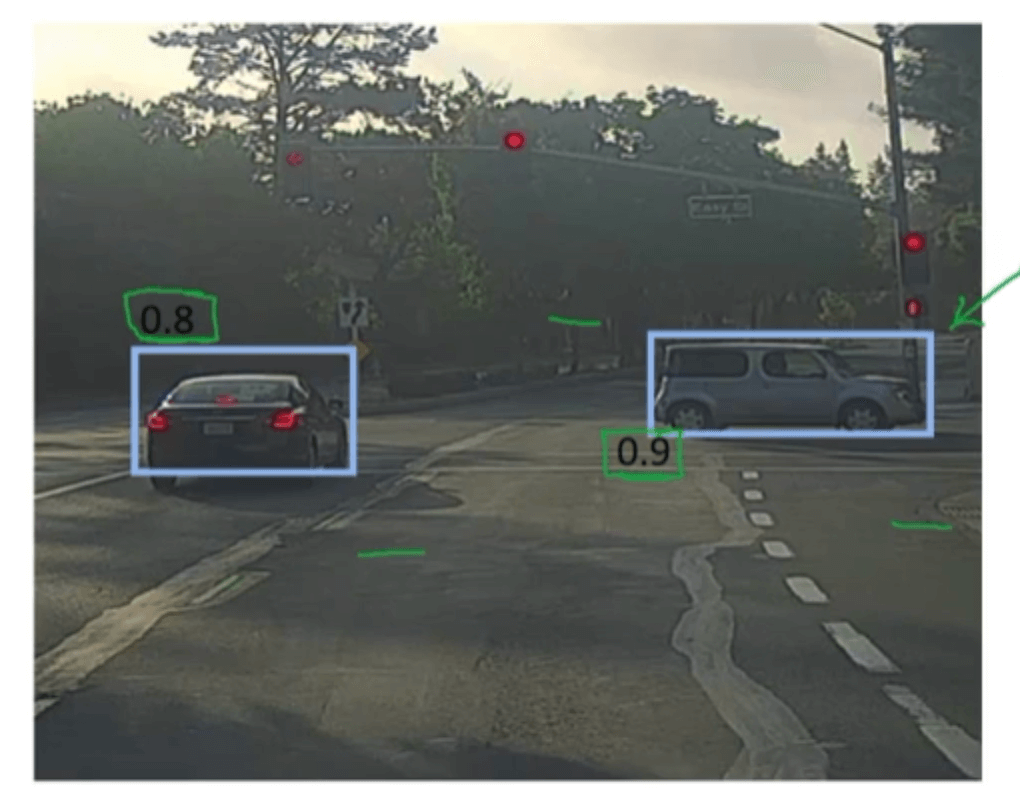
当存在多个不同类别的对象时,分别对每个对象进行NMS。
4.Anchor Box
目前为止,我们只讨论了每个格子只能检测出一个对象的情况。那么如何让一个格子检测出多个对象呢?这时就需要引入anchor box了。
假设我们有如下一张图(依旧使用$3 \times 3$的网格),汽车和行人的中点位于同一个格子中:

如果我们还按第1部分定义的label,则无法同时预测两个对象。为了解决这个问题,我们事先定义两个不同形状的anchor box:
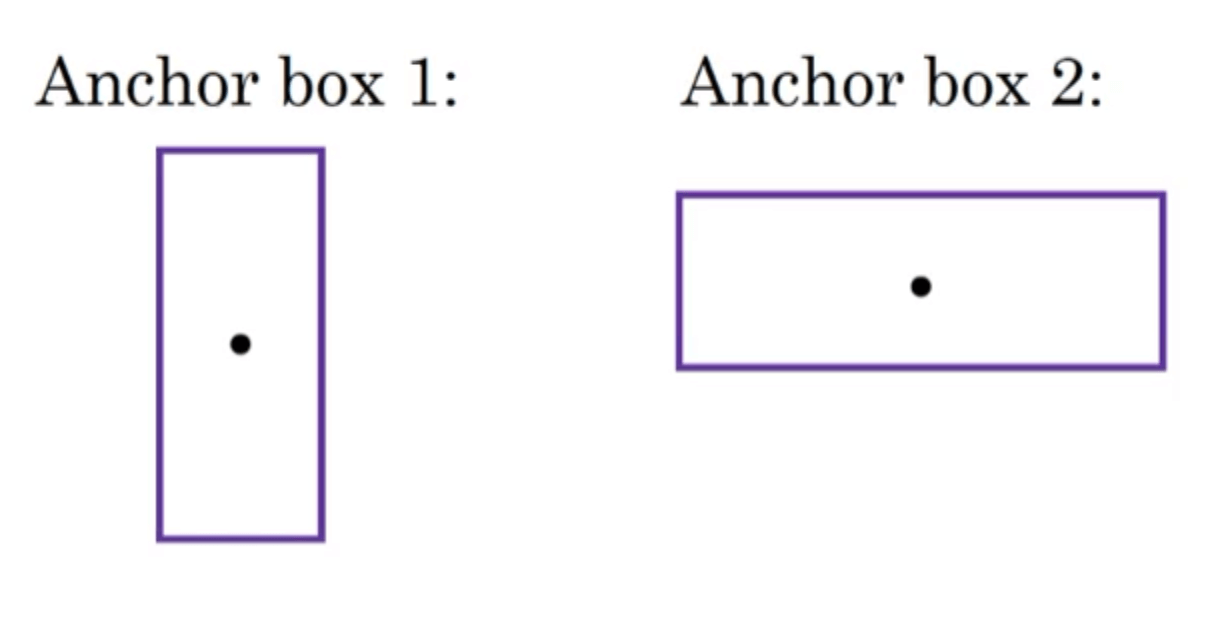
⚠️anchor box的个数与每个格子中可能出现的最多目标数量相同。实际项目中,会用更多的anchor box。
同时将label复制为原来的两倍,第一组参数(前八个参数)关联anchor box1,第二组参数(后八个参数)关联anchor box2:
\[y=\begin{bmatrix} P_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \\ P_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \end{bmatrix}\]因为行人的形状更类似于anchor box1,因此我们可以用前八个参数表示行人。同理,使用后八个参数表示汽车。也就是说,每个目标都会被分配一个格子和anchor box(该anchor box和该目标有着最高的IoU)。因此,现在的输出维度为$3\times 3 \times 16$(或$3\times 3 \times 2 \times 8$)。
针对以下两种情况,算法可能会处理不好:
- anchor box的个数小于每个格子中可能出现的最多目标数量。比如预先设定了2个anchor box,但是同一个格子里出现了3个目标。
- 同一个格子里的多个目标被分配到同一个anchor box。
那么该如何选择anchor box呢?
- 人工指定。
- k-means算法。
5.YOLO算法
至此,我们已经学习了YOLO算法中所有重要的组件。接下来我们从更宏观的角度介绍下YOLO算法。
YOLOv1:博客讲解。
假设输入为$448\times 448 \times 3$,使用$7\times 7$的网格:
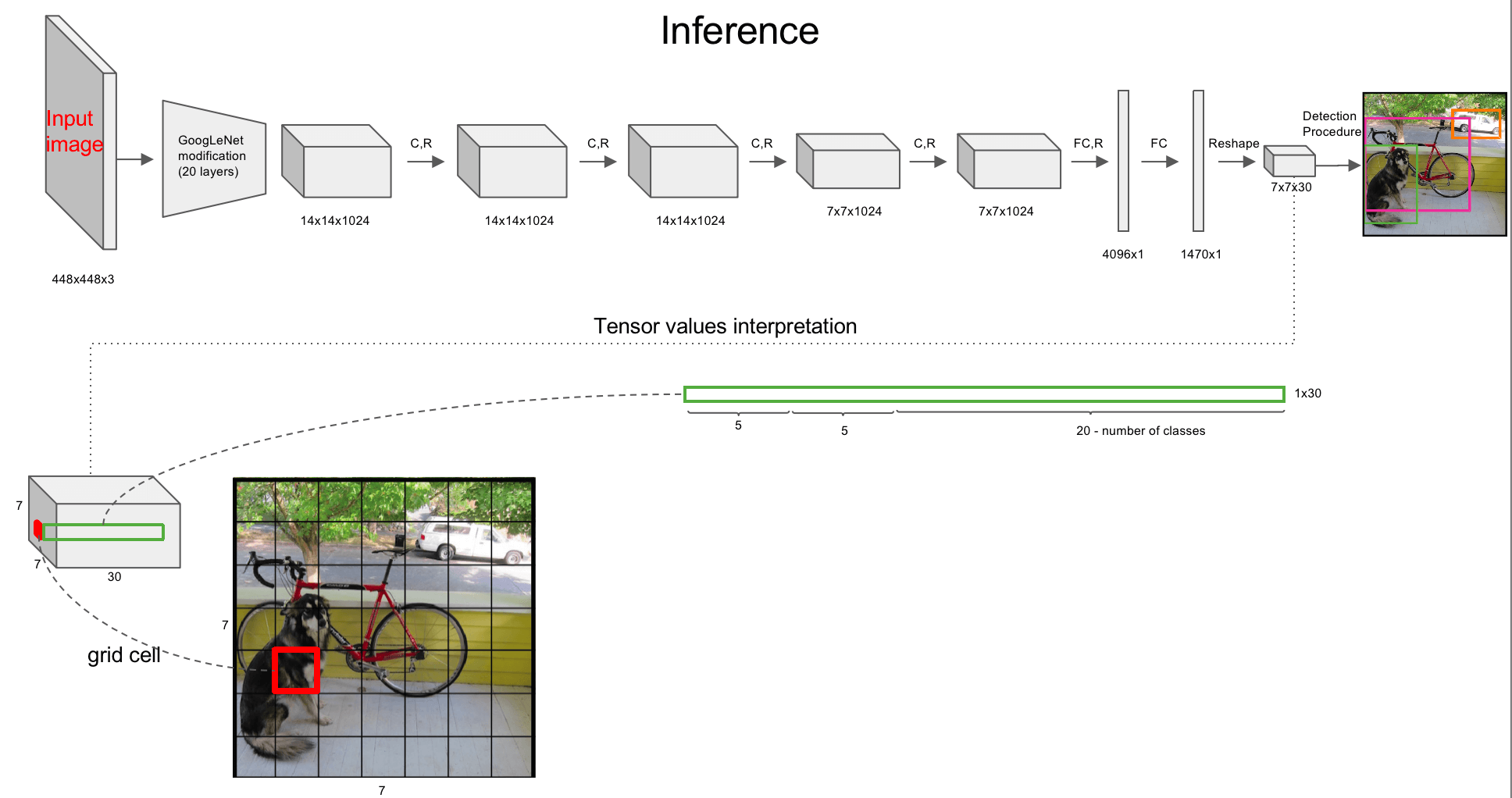
输出维度为$7\times 7 \times 30$,假设我们使用了两个anchor box,任务一共包含20个类别,即$5+5+20=30$。
👉第一个5的含义(即第一个anchor box):
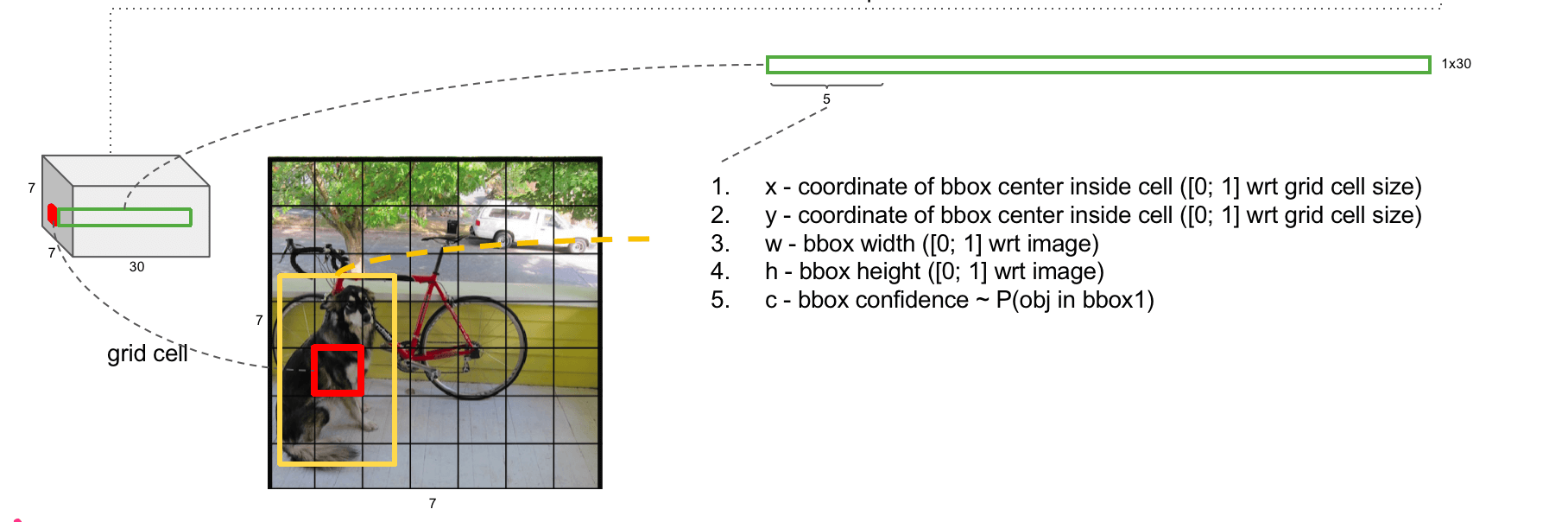
👉第二个5的含义(即第二个anchor box):

👉20的含义:即一共有20个类别。
在预测阶段,每个grid cell都会预测出来两个bounding box(为方便做图,简化为$3\times 3$的grid):

去掉概率较低的bounding box:

对行人和汽车这两个类别分别执行NMS,得到最终的预测结果:
