【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.核函数
在之前的博客中,我们假设训练样本是线性可分的,即存在一个划分超平面能将训练样本正确分类。然而在现实任务中,原始样本空间内也许并不存在一个能正确划分两类样本的超平面。例如下图中的“异或”问题就不是线性可分的:
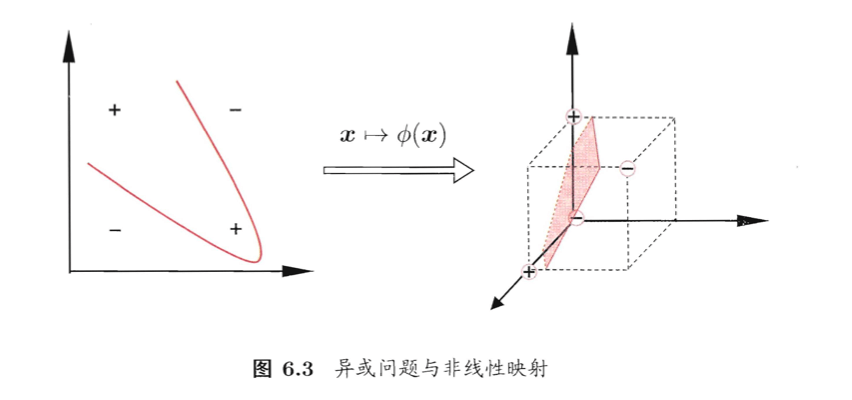
对这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。例如在上图中,若将原始的二维空间映射到一个合适的三维空间,就能找到一个合适的划分超平面。⚠️幸运的是,如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
令$\phi (\mathbf x)$表示将$\mathbf x$映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为:
\[f(\mathbf x)=\mathbf w ^T \phi (\mathbf x)+b \tag{1}\]其中$\mathbf w,b$是模型参数,类似【机器学习基础】第十六课:支持向量机之间隔与支持向量中学到的SVM的基本型,有:
\[\begin{align*} &\min \limits_{\mathbf w,b} \quad \frac{1}{2} \lVert \mathbf w \rVert ^2 \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& y_i(\mathbf w^T \phi (\mathbf x_i) +b) \geqslant 1,i=1,2,...,m \\ \end{array} \end{align*} \tag{2}\]其对偶问题是:
\[\begin{align*} &\max \limits_{\mathbf \alpha} \quad \sum_{i=1}^m \alpha_i-\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \phi(\mathbf x_i)^T \phi(\mathbf x_j) \\ & \begin{array}{r@{\quad}l@{}l@{\quad}l} s.t.& \sum_{i=1}^m \alpha_i y_i=0 \\ & \alpha_i \geqslant 0,i=1,2,...,m \\ \end{array} \end{align*} \tag{3}\]求解式(3)涉及到计算$\phi (\mathbf x_i)^T \phi (\mathbf x_j)$,这是样本$\mathbf x_i$与$\mathbf x_j$映射到特征空间之后的内积。由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算$\phi (\mathbf x_i)^T \phi (\mathbf x_j)$通常是困难的。为了避开这个障碍,可以设想这样一个函数:
\[\kappa (\mathbf x_i,\mathbf x_j)=<\phi (\mathbf x_i)^T,\phi (\mathbf x_j)>=\phi (\mathbf x_i)^T \phi (\mathbf x_j) \tag{4}\]即$\mathbf x_i$与$\mathbf x_j$在特征空间的内积等于它们在原始样本空间中通过函数$\kappa (\cdot,\cdot)$计算的结果。有了这样的函数,我们就不必直接去计算高维甚至无穷维特征空间中的内积,于是式(3)可重写为:
\[\begin{align*} &\max \limits_{\mathbf \alpha} \quad \sum_{i=1}^m \alpha_i-\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa (\mathbf x_i,\mathbf x_j) \\ & \begin{array}{r@{\quad}l@{}l@{\quad}l} s.t.& \sum_{i=1}^m \alpha_i y_i=0 \\ & \alpha_i \geqslant 0,i=1,2,...,m \\ \end{array} \end{align*} \tag{5}\]求解后即可得到:
\[\begin{align} f(\mathbf x) & = \mathbf w^T \phi(\mathbf x) +b \\ & = \sum_{i=1}^m \alpha_i y_i \phi (\mathbf x_i)^T \phi (\mathbf x) + b \\ & = \sum_{i=1}^m \alpha_i y_i \kappa (\mathbf x, \mathbf x_i) + b \end{align} \tag{6}\]这里的函数$\kappa(\cdot,\cdot)$就是“核函数(kernel function)”。式(6)显示出模型最优解可通过训练样本的核函数展开,这一展式亦称“支持向量展式(support vector expansion)”。
显然,若已知合适映射$\phi (\cdot)$的具体形式,则可写出核函数$\kappa(\cdot,\cdot)$。但在现实任务中我们通常不知道$\phi (\cdot)$是什么形式,那么,合适的核函数是否一定存在呢?什么样的函数能做核函数呢?我们有下面的定理:
核函数定理:令$\chi$为输入空间,$\kappa(\cdot,\cdot)$是定义在$\chi \times \chi$上的对称函数,则$\kappa$是核函数当且仅当对于任意数据$D=\{\mathbf x_1,\mathbf x_2,…,\mathbf x_m \}$,“核矩阵”(kernel matrix)$K$总是半正定的:
\[\mathbf K = \begin{bmatrix} \kappa (\mathbf x_1,\mathbf x_1) & \cdots & \kappa (\mathbf x_1,\mathbf x_j) & \cdots & \kappa (\mathbf x_1,\mathbf x_m) \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ \kappa (\mathbf x_i,\mathbf x_1) & \cdots & \kappa (\mathbf x_i,\mathbf x_j) & \cdots & \kappa (\mathbf x_i,\mathbf x_m) \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ \kappa (\mathbf x_m,\mathbf x_1) & \cdots & \kappa (\mathbf x_m,\mathbf x_j) & \cdots & \kappa (\mathbf x_m,\mathbf x_m) \end{bmatrix}\]上述定理表明,只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射$\phi$。换言之,任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间”(Reproducing Kernel Hilbert Space,简称RKHS)的特征空间。
通过前面的讨论可知,我们希望样本在特征空间内线性可分,因此特征空间的好坏对支持向量机的性能至关重要。需注意的是,在不知道特征映射的形式时,我们并不知道什么样的核函数是合适的,而核函数也仅是隐式地定义了这个特征空间。
⚠️于是,“核函数选择”成为支持向量机的最大变数。若核函数选择不合适,则意味着将样本映射到了一个不合适的特征空间,很可能导致性能不佳。
这方面有一些基本的经验,例如对文本数据通常采用线性核,情况不明时可先尝试高斯核。
常用的核函数:

$d=1$时退化为线性核,高斯核亦称RBF核。
此外,还可通过函数组合得到,例如:
👉若$\kappa_1$和$\kappa_2$为核函数,则对于任意正数$\gamma_1,\gamma_2$,其线性组合
\[\gamma_1 \kappa_1 + \gamma_2 \kappa_2\]也是核函数。
👉若$\kappa_1$和$\kappa_2$为核函数,则核函数的直积
\[\kappa_1 \otimes \kappa_2 (\mathbf x,\mathbf z)=\kappa_1(\mathbf x,\mathbf z) \kappa_2 (\mathbf x,\mathbf z)\]也是核函数。
👉若$\kappa_1$为核函数,则对于任意函数$g(\mathbf x)$,
\[\kappa (\mathbf x,\mathbf z)=g(\mathbf x)\kappa_1 (\mathbf x,\mathbf z)g(\mathbf z)\]也是核函数。
2.直积
“直积”又称“笛卡尔乘积”:表示为$X \otimes Y$,第一个对象是$X$的成员而第二个对象是$Y$的所有可能有序对的其中一个成员。
例如,$A=\{a,b \},B=\{ 0,1,2 \}$,则:
\[A \otimes B=\{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)\}\] \[B \otimes A=\{(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)\}\]