本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.优化与凸优化简介
1.1.优化问题基本形式
优化问题的一般形式:
\[最小化:f_0(x)\] \[条件:f_i(x) \leqslant b_i , i=1,...,m\]其中$f_0(x)$为目标函数,条件里的不等式是限制条件。优化问题举例:极大似然估计、最小二乘法。
1.2.凸优化问题基本形式
凸优化问题的一般形式:
\[最小化:f_0(x)\] \[条件:f_i(x) \leqslant b_i , i=1,...,m\]其中$f_0(x)$为目标函数,条件里的不等式是限制条件。
- 凸优化问题的条件:$f_0,f_1,…,f_m$都是凸函数。
- 凸优化问题的特点:局部最优等价于全局最优。
- 凸优化问题的求解:几乎总有现成的工具来求解。
1.3.凸优化的应用
- 凸优化问题逼近非凸优化问题,寻找非凸问题的初始点。
- 利用对偶问题的凸性给原问题提供下界估计。
- 凸优化问题可以给非凸问题带来一些启发。
针对应用1,假设代价函数的图像如下所示:

存在很多局部最优点。我们可以将其近似为一个凸函数,然后求其极值点作为优化问题的初始点(例如梯度下降法或牛顿法的起始点):

2.凸集合与凸函数基本概念
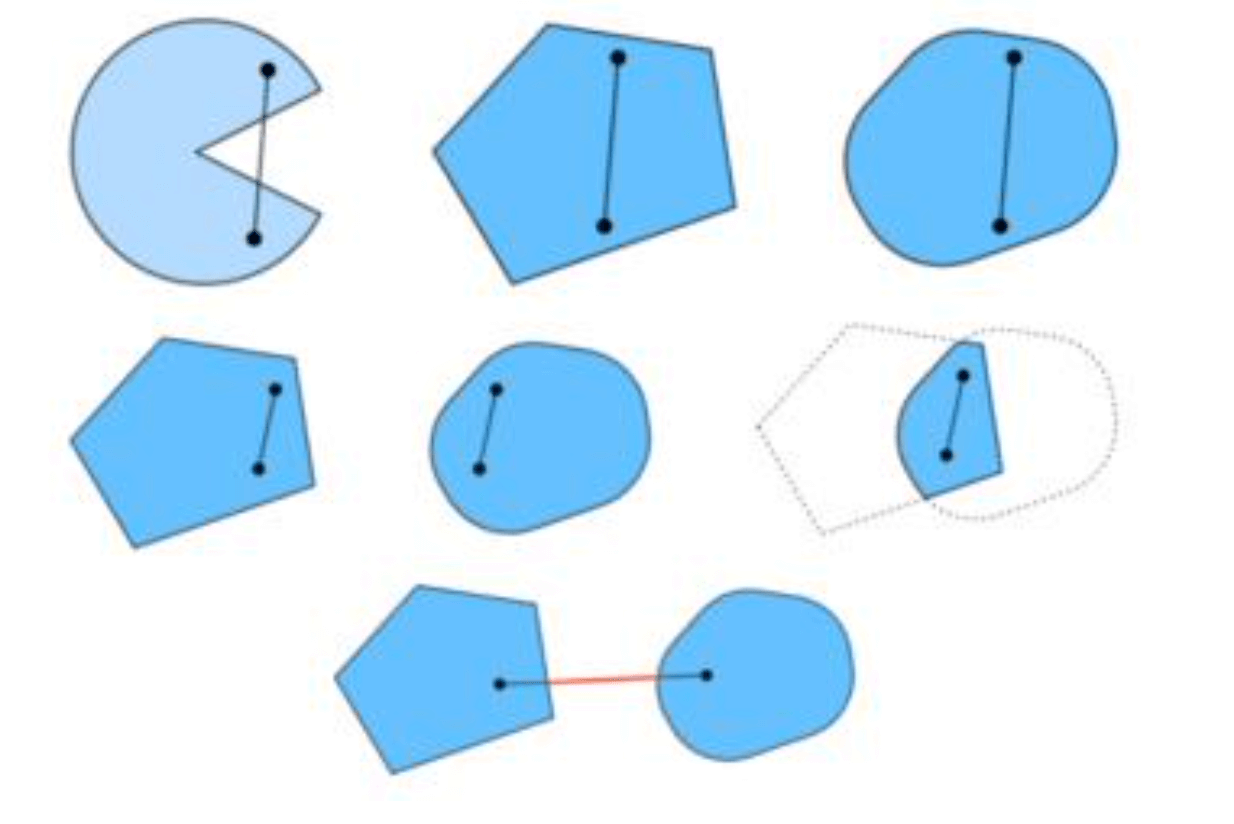
👉凸集合定义:如果一个集合$\Omega$中任何两个点之间的线段上任何一个点还属于$\Omega$,那么$\Omega$就是一个凸集合。即:
\[\lambda x_1+(1-\lambda) x_2 \in \Omega,\forall x_1,x_2 \in \Omega,\lambda \in (0,1)\]例如下图中,第一行的第一个集合和最后一行的集合都不是凸集合,其余均为凸集合:
👉凸函数定义:如果一个函数$f$定义域$\Omega$是凸集,而且对于任何两点,以及两点之间线段上任意一个点都有:
\[f(\lambda x_1+(1-\lambda)x_2) \leqslant \lambda f(x_1)+(1-\lambda) f(x_2),\forall x_1,x_2 \in \Omega,\lambda \in (0,1)\]👉函数的上境图:假设$f$是一个定义在$\Omega$上的函数,区域$\{(x,y):y \geqslant f(x) ,\forall x \in \Omega \}$就是$f$的上境图。即上境图就是函数图像上方的部分区域。
❗️凸集合与凸函数的关系:一个函数是凸函数当且仅当$f$的上境图是凸集合。
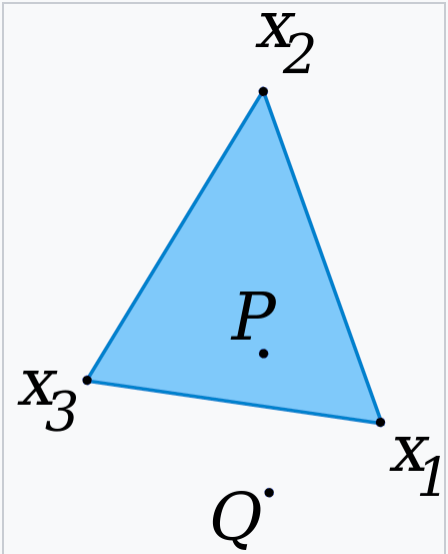
👉凸组合:对于任何$n$个点$\{ x_i \}^n_{i=1}$,以及权重系数$\{ w_i \}^n_{i=1}$。若权重系数非负$w_i \geqslant 0$而且$\sum^n_{i=1} w_i=1$,则线性组合
\[S=\sum^n_{i=1} w_i x_i\]为一个凸组合。从几何意义来说,凸组合就是这$n$个点所围成的图形中的任意一点。例如,下图中有$x_1,x_2,x_3$三个点,这三个点所围成的蓝色三角形中的任意一点$P$是这三个点的一种凸组合,而点$Q$不是:
👉集合的凸包:$n$个点$\{ x_i \}^n_{i=1}$的全部凸组合就构成$\{ x_i \}^n_{i=1}$的凸包。
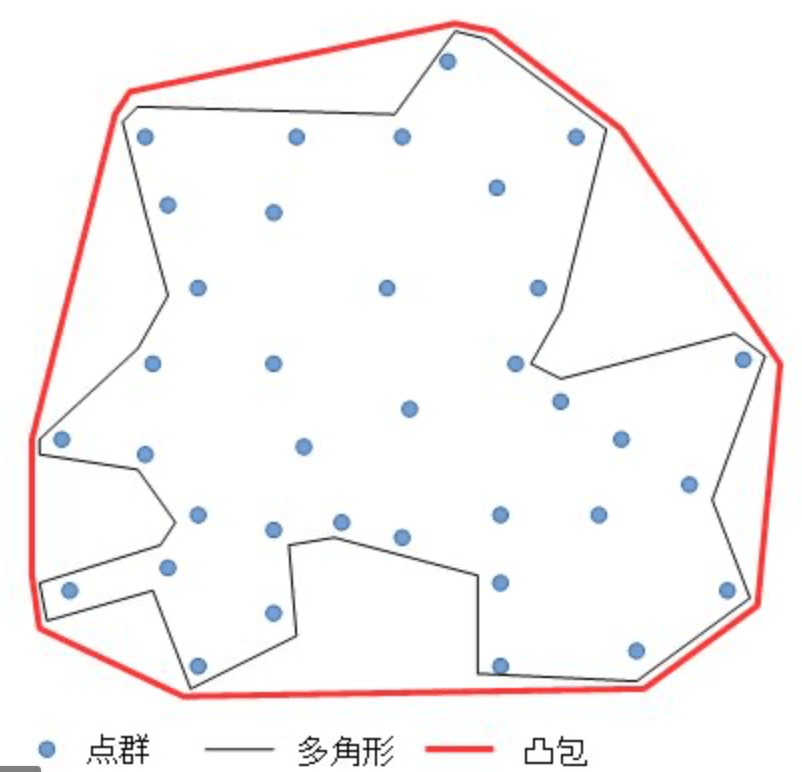
👉集合的凸包的性质:若$\bar {C}$是$C$的凸包,那么,
- $C \subset \bar {C}$
- $C$的支撑平面也是$\bar {C}$的支撑平面,反之亦然

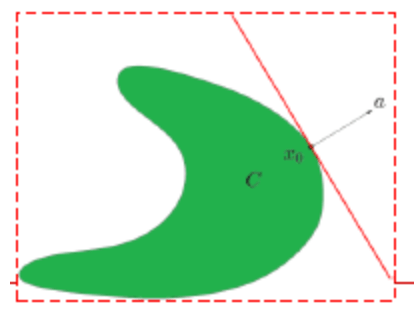
支撑超平面:设集合$C$,$x_0$为$C$边界上的点。若存在$a \neq 0$,满足对任意$x \in C$,都有$a^T x \leqslant a^T x_0$成立,则称超平面$\{ x \mid a^T x = a^T x_0 \}$为集合$C$在点$x_0$处的支撑超平面。
凸集边界上任意一点,均存在支撑超平面。反之,若一个闭的非中空(内部点不为空)集合,在边界上的任意一点存在支撑超平面,则该集合为凸集。
👉函数的凸闭包:如果$C$是函数$f$的上境图,$\bar {C}$是$C$的凸包,那么以$\bar {C}$为上境图的函数称为$f$的凸闭包。

上图中,$g(x)$为$f(x)$的凸闭包。
👉函数的凸闭包的性质:若$g$是$f$的凸闭包,那么,
- $g \leqslant f$
- $\inf g = \inf f$
3.凸集合与凸函数的对应性质
3.1.凸组合
👉凸集合性质:假设$\Omega$是一个凸集合,那么$\Omega$任何子集的凸包仍包含于$\Omega$。
👉凸函数性质:琴生不等式。
琴生不等式的应用举例:
应用一,证明算数平均大于等于几何平均,即对于正数$a_1,…,a_n$,
\[\frac{\sum^n_{i=1} a_i}{n} \geqslant (\prod ^n _{i=1} a_i)^{\frac{1}{n}}\]证明如下,以凸函数$-\ln (x)$为例:
\[-\ln (\frac{1}{n} (a_1+...+a_n) ) \leqslant \frac{1}{n} \sum^n_{i=1} -\ln (a_i)\] \[\ln (\frac{1}{n} (a_1+...+a_n) ) \geqslant \frac{1}{n} \sum^n_{i=1} \ln (a_i)\] \[exp(\ln (\frac{1}{n} (a_1+...+a_n) )) \geqslant exp(\frac{1}{n} \sum^n_{i=1} \ln (a_i))\] \[\frac{1}{n} (a_1+...+a_n) \geqslant (a_1 ... a_n) ^{\frac{1}{n}}\]应用二,证明柯西不等式:
\[(\sum^n_{i=1} a^2_i)(\sum^n_{i=1} b^2_i) \geqslant (\sum^n_{i=1} a_i b_i)^2\]证明如下,以函数$f(x)=x^2$为例,假设有:
\[w_i=\frac{b_i^2}{\sum^n_{i=1} (b_i^2)};x_i=\frac{a_i}{b_i}\]根据琴生不等式有:
\[f(\sum_{i=1}^n w_i x_i) \leqslant \sum_{i=1}^n w_i f(x_i)\] \[(\sum_{i=1}^n \frac{b_i a_i}{\sum^n_{i=1} (b_i^2)})^2 \leqslant \sum_{i=1}^n \frac{ a_i^2}{\sum^n_{i=1} (b_i^2)}\] \[(\frac{\sum_{i=1}^n( b_i a_i)}{\sum^n_{i=1} (b_i^2)})^2 \leqslant \frac{ \sum_{i=1}^n(a_i^2)}{\sum^n_{i=1} (b_i^2)}\] \[(\sum_{i=1}^n( b_i a_i))^2 \leqslant \frac{ \sum_{i=1}^n(a_i^2)}{\sum^n_{i=1} (b_i^2)} \cdot (\sum^n_{i=1} (b_i^2))^2\] \[(\sum_{i=1}^n( b_i a_i))^2 \leqslant \sum_{i=1}^n(a_i^2) \cdot \sum^n_{i=1} (b_i^2)\]3.2.集合相交
👉凸集合性质:任意多个凸集合的交集仍是凸集合。
👉凸函数性质:
- 任意多个凸函数的逐点上确界仍是凸函数。
- 固定一个凸函数的若干个变量,所得的函数仍然是凸函数。
- 凸函数的子水平集都是凸集合。
逐点上确界:
\[f(x)=\sup \{ f_1(x) ,..., f_n(x) \}\]逐点最大值:
\[f(x)=\max \{ f_1(x) ,..., f_n(x) \}\]
性质1示意图:

性质2,例如有如下凸函数$z$,固定变量$x$(即$x$为某一定值),剩余的函数$z=y^2$依旧是凸函数:

水平集(level set):集合
\[\{ (x_1,...,x_n) \mid f(x_1,...,x_n) = c \}\]被称为水平集,其中,$c$为常数。
子水平集(sublevel set):集合
\[\{ (x_1,...,x_n) \mid f(x_1,...,x_n) \leqslant c \}\]被称为子水平集,其中,$c$为常数。
3.3.线性组合
👉凸集合性质:假设$T:V\to W$是一个线性映射,则
- 若$\Omega _V$是$V$中的凸集合,则$\Omega _W=T(\Omega _V)$是$W$中的凸集合。
- 若$\Omega _W$是$W$中的凸集合,则$\Omega _V=T^{-1}(\Omega _W)$是$V$中的凸集合。
👉凸函数性质:
- 凸函数的非负线性组合仍是凸函数,$f_1,…,f_k$是凸函数,而且$w_i \geqslant 0$,则$\sum^k_{i=1} w_i f_i$也是凸函数。
- 若$f:\mathbb R ^n \to \mathbb R$是凸函数,$A \in \mathbb R ^{n\times m},b\in \mathbb R ^n$,那么复合函数$g(x)=f(Ax+b)$还是凸函数。
3.4.微分
👉凸集合性质:
- 若凸集合$\Omega$的边界$C$是一个可微曲线,则$C$在任何一点上的切线(平面)都是这个凸集合的支撑线(平面)。
- 若凸集合$\Omega$的边界$C$是一个二阶可微曲线,则$C$在任何一点上的曲率向量都指向$\Omega$内部。
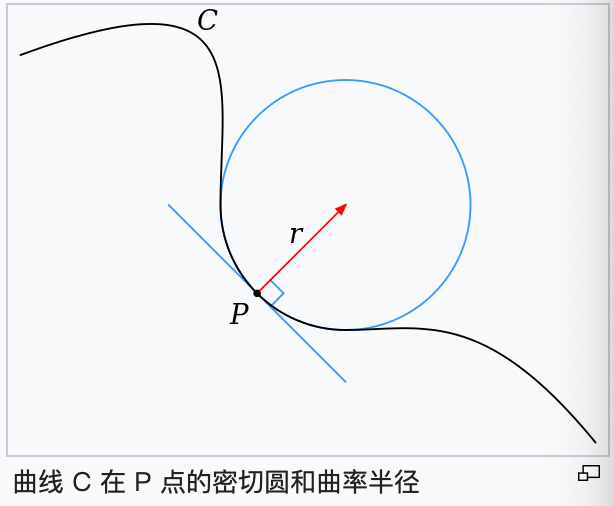
平面曲线的曲率:圆上每一点处的弯曲程度都相同,半径越小弯曲得越厉害,所以可以用半径的倒数来定量描述圆的弯曲程度,即曲率。直线可以看作半径无限大的圆,所以直线的曲率为0。对于任意形状的曲线,每一点处的弯曲程度一般是不同的。对曲线$C$上任一点$P$,在其附近再找$C$上的两个点$P_1,P_2$,这三点总能确定一个圆(三点共线时确定一条直线,但可以把直线看作半径无限大的广义的圆)。当$P_1,P_2$无限接近点$P$时,相应的圆也有一个极限,这个极限圆就是在点$P$处最接近曲线$C$的圆,称为密切圆。密切圆的曲率就是曲线$C$在点$P$处的曲率。
👉凸函数性质:
- 若一个凸函数一阶可微,那么凸函数的一阶近似不大于函数本身:
- 若一个凸函数二阶可微,那么这个函数的二阶导数(Henssen矩阵)非负(半正定)。
3.5.光学投影
👉凸集合性质:
- 若$\Omega$是凸集合,那么$\Omega$在任何一个平面上的投影仍是凸集合(平行光源投影)。
- 若$\Omega \subset \mathbb R^n$是凸集合,那么$\Omega _{\hat n}=\{ (x_1 /x_n ,…,x_{n-1} / x_n,1) : (x_1,…,x_n) \in \Omega 且 x_n \neq 0 \}$也是凸集合(点光源投影)。
- 若$\Omega \subset \mathbb R ^n$是一个凸集合,那么锥体$tx :x \in \Omega,t\in \mathbb R_+$也是个凸集合(点光源)。
关于性质2,以下图为例,凸集合经过原点小孔成像到$x_n=1$的超平面,得到的投影仍然是一个凸集合,但是维度相比之前减少了一维:

性质3示意图见下,得到的锥体也是凸集合:

👉凸函数性质:
- 若$f(x,y)$是凸函数,那么$g(x)= \inf _{(x,y)\in \Omega} f(x,y)$,也是凸函数(对应凸集合性质1)。
- 若$f: \mathbb R ^n \to \mathbb R$是凸函数,那么$g(x,t)=tf(x/t):\mathbb R^{n+1} \to \mathbb R$也是个凸函数(对应凸集合性质3)。
4.凸集分离定理
若$C,D$分别为$\mathbb R^n$中的两个不交的非空凸集合,即$C \cap D = \varnothing$,则一定存在向量$a\in \mathbb R ^n$以及实数$b\in \mathbb R$使得任何$x_C \in C,x_D \in D$有$a^T x_C \leqslant b$以及$a^T x_D \geqslant b$。
定理中不等式的几何意义在于$C,D$分别位于超平面$a^T x=b$的两边。
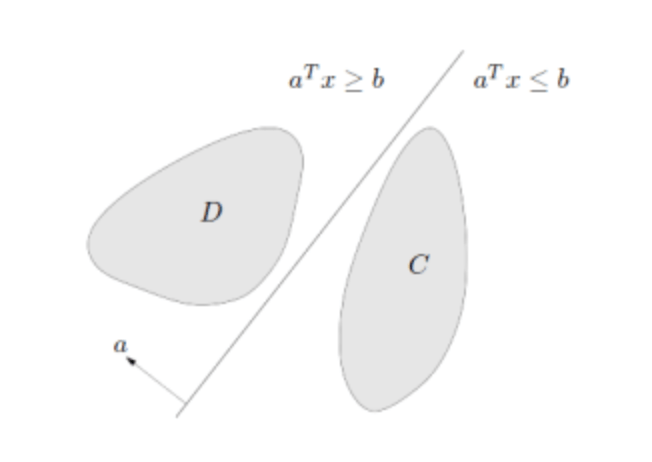
凸集分离定理是凸集理论的最基本的定理,它是指在很弱的条件下,两个不相交的凸集总可用超平面分离。