本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.卷积应用:图像边缘提取
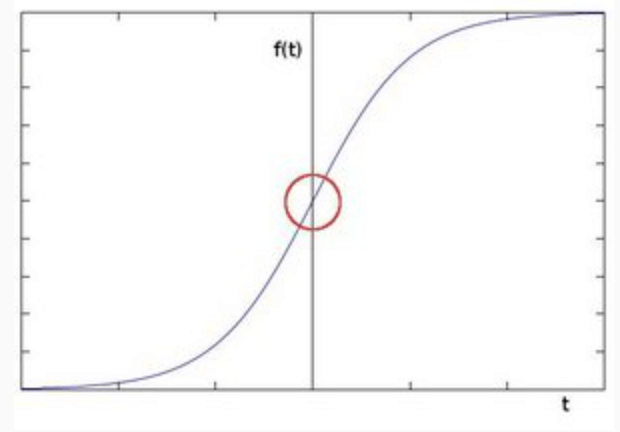
图像的边缘是像素值发生跃迁的地方,是图像的显著特征之一,在图像特征提取、对象检测、模式识别等方面都有重要的作用。如下图红圈处所示,即为图像的一个边缘:

如何捕捉/提取边缘:对图像求它的一阶导数。$\delta=f(x)-f(x-1)$,$\delta$越大,说明像素在X方向变化越大,边缘信号越强。例如上图红圈处的像素变化以及其一阶导数变化:
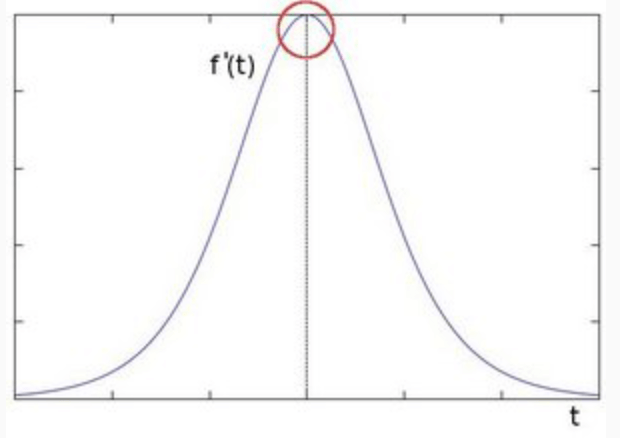
Sobel算子便可用于图像边缘提取。
2.Sobel算子
Sobel算子是离散微分算子(discrete differentiation operator),用来计算图像灰度的近似梯度。
Sobel算子功能集合高斯平滑和微分求导。其又被称为一阶微分算子,求导算子(拉普拉斯是二阶求导算子),在水平和垂直两个方向上求导,得到图像X方向与Y方向梯度图像。
Sobel算子包含两组$3\times 3$的矩阵,分别为横向及纵向,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。如果以$\mathbf {A}$代表原始图像,$\mathbf {G_x}$及 $\mathbf {G_y}$分别代表经横向及纵向边缘检测的图像,其公式如下:
\[\mathbf {G_x}=\begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \\ \end{bmatrix} * \mathbf A\] \[\mathbf {G_y}=\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \\ \end{bmatrix} * \mathbf A\]图像的每一个像素的横向及纵向梯度近似值可用以下的公式结合,来计算梯度的大小。
\[\mathbf G = \sqrt {\mathbf {G_x}^2 + \mathbf {G_y}^2 }\]在实际应用中,为了加快计算速度,上式可简化为:
\[\mathbf G =\lvert \mathbf {G_x} \rvert + \lvert \mathbf {G_y} \rvert\]3.Scharr算子
虽然Sobel算子可以有效的提取图像边缘,但是对图像中较弱的边缘提取效果较差。因此为了能够有效的提取出较弱的边缘,需要将像素值间的差距增大,因此引入Scharr算子。Scharr算子是对Sobel算子差异性的增强,因此两者在检测图像边缘的原理和使用方式上相同。
\[\mathbf {G_x}=\begin{bmatrix} -3 & 0 & +3 \\ -10 & 0 & +10 \\ -3 & 0 & +3 \\ \end{bmatrix} * \mathbf A\] \[\mathbf {G_y}=\begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ +3 & +10 & +3 \\ \end{bmatrix} * \mathbf A\]4.API
👉Sobel算子:
1
2
3
4
5
6
7
8
9
10
11
cv::Sobel(
InputArray Src,//输入图像
OutputArray dst,//输出图像,大小与输入图像一致
int depth,//输出图像深度。如果输入图像的深度是CV_8U的灰度图像,经过Sobel算子计算之后,输出的值可能在0-255的范围之外,所以,输出图像的深度可能要比输入图像的深度更大。
int dx,//X方向,几阶导数
int dy,//Y方向,几阶导数
int ksize,//Sobel算子kernel大小,必须是1,3,5,7
double scale=1,//kernel中的值放大或缩小的倍数
double delta=0,//算出来的像素值再加上delta
int borderType=BORDER_DEFAULT
)
👉Scharr算子:
1
2
3
4
5
6
7
8
9
10
cv::Scharr(
InputArray Src,//输入图像
OutputArray dst,//输出图像,大小与输入图像一致
int depth,//输出图像深度
int dx,//X方向,几阶导数
int dy,//Y方向,几阶导数
double scale=1,
double delta=0,
int borderType=BORDER_DEFAULT
)
cv::Scharr和cv::Sobel参数基本一样。⚠️注意:两个函数的输出图像深度只能大于等于原来的图像,不能比原来的图像小!
两个函数的第四个参数dx和第五个参数dy是提取X方向边缘还是Y方向边缘的标志,该函数要求这两个参数只能有一个参数为1,并且不能同时为0,否则函数将无法提取图像边缘。
此外,cv::Scharr函数默认的滤波器尺寸为$3\times 3$,并且无法修改。
5.不同尺寸的Sobel算子
边缘检测类似微分运算,其本质就是检测图像亮度的变化,因此噪声必然会对检测效果产生一定影响。为了避免噪声的影响,在构造边缘检测算子时不仅要考虑差分处理,还得要考虑平滑处理。这样既能滤除噪声还能检测边缘。在同时期的边缘检测算法中,Sobel算子被认为是最好的检测模板,它除了考虑差分因素还兼顾了最优的平滑系数。
构造Sobel算子的理论基础是帕斯卡三角形(Pascal’s triangle):
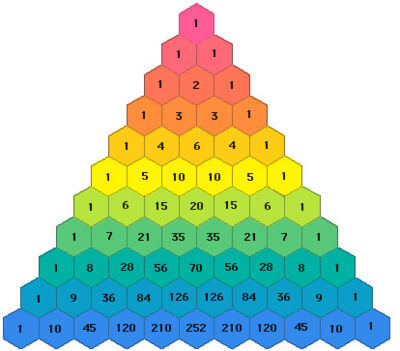
帕斯卡三角形的构建公式为($n$为行数,$k$为列数):
\[P(k,n)=\frac{n!}{[(n-k)! * k!]},\ if \ k \geqslant 0 \ and \ k \leqslant n\] \[P(k,n)=0,\ otherwise\]假设Sobel算子的大小为$w\times w$。首先计算算子的平滑系数:
\[S_k=P(k,w-1)\]然后计算算子的差分系数:
\[D_k=P(k,w-2)-P(k-1,w-2)\]则Sobel算子的横向模板:
\[Sobel(x,y)=S_y D_x\]Sobel算子的纵向模板:
\[Sobel(x,y)=S_x D_y\]以$5\times 5$的Sobel算子的计算为例:
\[S_0=P(0,4)=1\] \[S_1=P(1,4)=4\] \[S_2=P(2,4)=6\] \[S_3=P(3,4)=4\] \[S_4=P(4,4)=1\] \[D_0=P(0,3)-P(-1,3)=1-0=1\] \[D_1=P(1,3)-P(0,3)=3-1=2\] \[D_2=P(2,3)-P(1,3)=3-3=0\] \[D_3=P(3,3)-P(2,3)=1-3=-2\] \[D_4=P(4,3)-P(3,3)=0-1=-1\]最终得到的$5\times 5$的Sobel算子(纵向)为:
\[\begin{bmatrix} 1 & 2 & 0 & -2 & -1 \\ 4 & 8 & 0 & -8 & -4 \\ 6 & 12 & 0 & -12 & -6 \\ 4 & 8 & 0 & -8 & -4 \\ 1 & 2 & 0 & -2 & -1 \\ \end{bmatrix}\]横向为其转置,不再赘述。