【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.软间隔
在之前的博客中,我们一直假定训练样本在样本空间或特征空间中是线性可分的,即存在一个超平面能将不同类的样本完全划分开。然而,在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分;退一步说,即便恰好找到了某个核函数使训练集在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。
缓解该问题的一个办法是允许支持向量机在一些样本上出错。为此,要引入“软间隔”(soft margin)的概念:
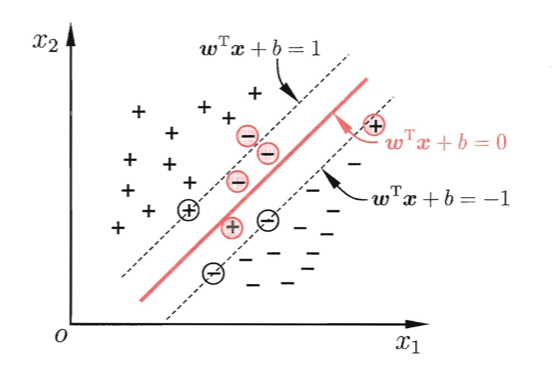
红色圈出了一些不满足约束的样本。
具体来说,之前介绍的支持向量机形式是要求所有样本均满足约束:
\[\left\{ \begin{array}{c} \mathbf w^T \mathbf x_i +b \geqslant +1, y_i=+1 \\ \mathbf w^T \mathbf x_i +b \leqslant -1, y_i=-1 \\ \end{array} \right. \tag{1}\]即所有样本都必须划分正确,这称为“硬间隔”(hard margin),而软间隔则是允许某些样本不满足约束:
\[y_i (\mathbf w^T \mathbf x_i +b) \geqslant 1 \tag{2}\]当然,在最大化间隔的同时,不满足约束的样本应尽可能少。于是,优化目标可写为:
\[\min \limits_{\mathbf w,b} \quad \frac{1}{2} \lVert \mathbf w \rVert ^2 + C \sum^m_{i=1} l_{0/1} (y_i (\mathbf w^T \mathbf x_i +b) -1) \tag{3}\]其中$C>0$是一个常数,$l_{0/1}$是“0/1损失函数”:
\[l_{0/1}(z) = \left \{ \begin{array}{l} 1, \quad if \ z<0; \\ 0, \quad otherwise \end{array} \right. \tag{4}\]显然,当C为无穷大时,式(3)迫使所有样本均满足约束(2)。因为C为无穷大时,要想最小化式(3),则$l_{0/1}(z)$中的$z$必须得大于等于0,这样才能消去式(3)中的第二项。于是式(3)等价于:
\[\begin{align*} &\min \limits_{\mathbf w,b} \quad \frac{1}{2} \lVert \mathbf w \rVert ^2 \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& y_i(\mathbf w^T \mathbf x_i +b) \geqslant 1,i=1,2,...,m \\ \end{array} \end{align*} \tag{5}\]当$C$取有限值时,式(3)允许一些样本不满足约束。
然而,$l_{0/1}$非凸、非连续、数学性质不太好,使得式(3)不易直接求解。于是,人们通常用其他一些函数来代替$l_{0/1}$,称为“替代损失”(surrogate loss)。常用的三种替代损失函数:
👉hinge损失:
\[l_{hinge}(z)=\max (0,1-z) \tag{6}\]👉指数损失(exponential loss):
\[l_{exp}(z)=exp(-z) \tag{7}\]👉对率损失(logistic loss):
\[l_{log}(z)=\log (1+exp(-z)) \tag{8}\]对率损失是对率函数的变形。
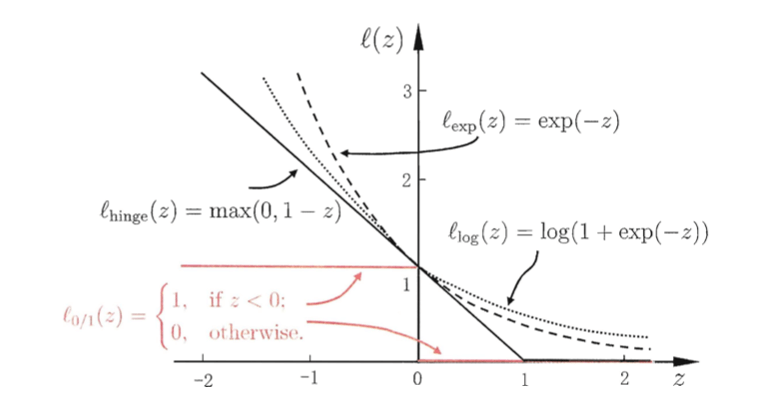
若采用hinge损失,则式(3)变成:
\[\min \limits_{\mathbf w,b} \quad \frac{1}{2} \lVert \mathbf w \rVert ^2 + C \sum^m_{i=1} \max (0,1-y_i (\mathbf w^T \mathbf x_i +b) ) \tag{9}\]要想最小化式(9),应该有$\max (0,1-y_i (\mathbf w^T \mathbf x_i +b) ) = 0$,即$1-y_i (\mathbf w^T \mathbf x_i +b) \leqslant 0$,即式(2)。
引入“松弛变量”(slack variables)$\xi _i \geqslant 0$,可将式(9)重写为:
\[\begin{align*} &\min \limits_{\mathbf w,b,\xi_i} \quad \frac{1}{2} \lVert \mathbf w \rVert ^2 +C \sum^m_{i=1} \xi_i \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& y_i(\mathbf w^T \mathbf x_i +b) \geqslant 1 - \xi_i \\& \xi_i \geqslant 0 , i=1,2,...,m \\ \end{array} \end{align*} \tag{10}\]这就是常用的(软间隔支持向量机)。
显然,式(10)中每个样本都有一个对应的松弛变量,用以表征该样本不满足约束式(2)的程度。但是,与式(5)相似,这仍是一个二次规划问题。于是,通过拉格朗日乘子法可得到式(10)的拉格朗日函数:
\[L(\mathbf w,b,\mathbf \alpha,\mathbf \xi,\mathbf \mu)=\frac{1}{2} \lVert \mathbf w \rVert ^2 +C \sum^m_{i=1} \xi_i + \sum^m_{i=1} \alpha_i (1- \xi_i - y_i(\mathbf w^T \mathbf x_i +b) )-\sum^m_{i=1} \mu_i \xi_i \tag{11}\]其中$\alpha_i \geqslant 0, \mu_i \geqslant 0$是拉格朗日乘子。
令$L(\mathbf w,b,\mathbf \alpha,\mathbf \xi,\mathbf \mu)$对$\mathbf w,b,\xi_i$的偏导为零可得:
\[\mathbf w=\sum^m_{i=1} \alpha_i y_i \mathbf x_i \tag{12}\] \[0=\sum^m_{i=1} \alpha_i y_i \tag{13}\] \[C=\alpha_i + \mu_i \tag{14}\]将式(12)-(14)代入式(11)即可得到式(10)的对偶问题:
\[\begin{align*} &\max \limits_{\mathbf \alpha} \quad \sum^m_{i=1}\alpha_i - \frac{1}{2} \sum^m_{i=1} \sum^m_{j=1} \alpha_i \alpha_j y_i y_j \mathbf x^T_i \mathbf x_j \\ & \begin{array}{l@{\quad}l@{}l@{\quad}l} s.t.& \sum^m_{i=1} \alpha_i y_i =0, \\& 0 \leqslant \alpha_i \leqslant C , i=1,2,...,m \\ \end{array} \end{align*} \tag{15}\]将式(15)与硬间隔的对偶问题对比可看出,两者唯一的差别就在于对偶变量的约束不同:前者是$0 \leqslant \alpha_i \leqslant C$,后者是$0 \leqslant \alpha _i$。于是,可采用和【机器学习基础】第十七课:支持向量机之对偶问题中同样的算法求解式(15);在引入核函数后能得到与【机器学习基础】第十八课:支持向量机之核函数中式(6)同样的支持向量机展式。
类似【机器学习基础】第十七课:支持向量机之对偶问题中式(1.8),对软间隔支持向量机,KKT条件要求:
\[\begin{equation} \left\{ \begin{array}{l} \alpha _i \geqslant 0,\\ \mu_i \geqslant 0,\\ y_i f(\mathbf x_i) -1 + \xi _i \geqslant 0,\\ \alpha_i (y_i f(\mathbf x_i) -1 + \xi _i) =0,\\ \xi_i \geqslant 0,\\ \mu_i \xi_i =0.\\ \end{array} \right. \end{equation} \tag{16}\]于是,对任意训练样本$(\mathbf x_i,y_i)$,总有$\alpha _i=0$或$y_i f(\mathbf x_i) = 1-\xi_i$。若$\alpha_i=0$,则该样本不会对$f(\mathbf x)$有任何影响;若$\alpha _i >0$,则必有$y_i f(\mathbf x_i)=1-\xi_i$,即该样本是支持向量:由式(14)可知,若$\alpha_i <C$,则$\mu_i >0$,进而有$\xi_i=0$,即该样本恰在最大间隔边界上;若$\alpha _i=C$,则有$\mu_i=0$,此时若$\xi _i \leqslant 1$则该样本落在最大间隔内部,若$\xi _i >1$则该样本被错误分类。由此可看出,软间隔支持向量机的最终模型仅与支持向量有关,即通过采用hinge损失函数仍保持了稀疏性。
2.正则化
我们还可以把式(3)中的0/1损失函数换成别的替代损失函数以得到其他学习模型,这些模型的性质与所用的替代函数直接相关,但它们具有一个共性:优化目标中的第一项用来描述划分超平面的“间隔”大小,另一项$\sum^m_{i=1} l (f(\mathbf x_i) y_i)$用来表述训练集上的误差,可写为更一般的形式:
\[\min \limits_{f} \quad \Omega (f)+C\sum^m_{i=1} l (f(\mathbf x_i) y_i) \tag{17}\]其中$\Omega (f)$称为“结构风险”(structural risk),用于描述模型$f$的某些性质(即正则化项);第二项$\sum^m_{i=1} l (f(\mathbf x_i) y_i)$称为“经验风险”(empirical risk),用于描述模型与训练数据的契合程度;$C$用于对二者进行折中(即正则化常数)。
3.松弛变量
松弛变量的引入常常是为了便于在更大的可行域内求解。本部分进一步介绍软间隔支持向量机。首先,弄清楚以下两个概念:
👉函数间隔和几何间隔:
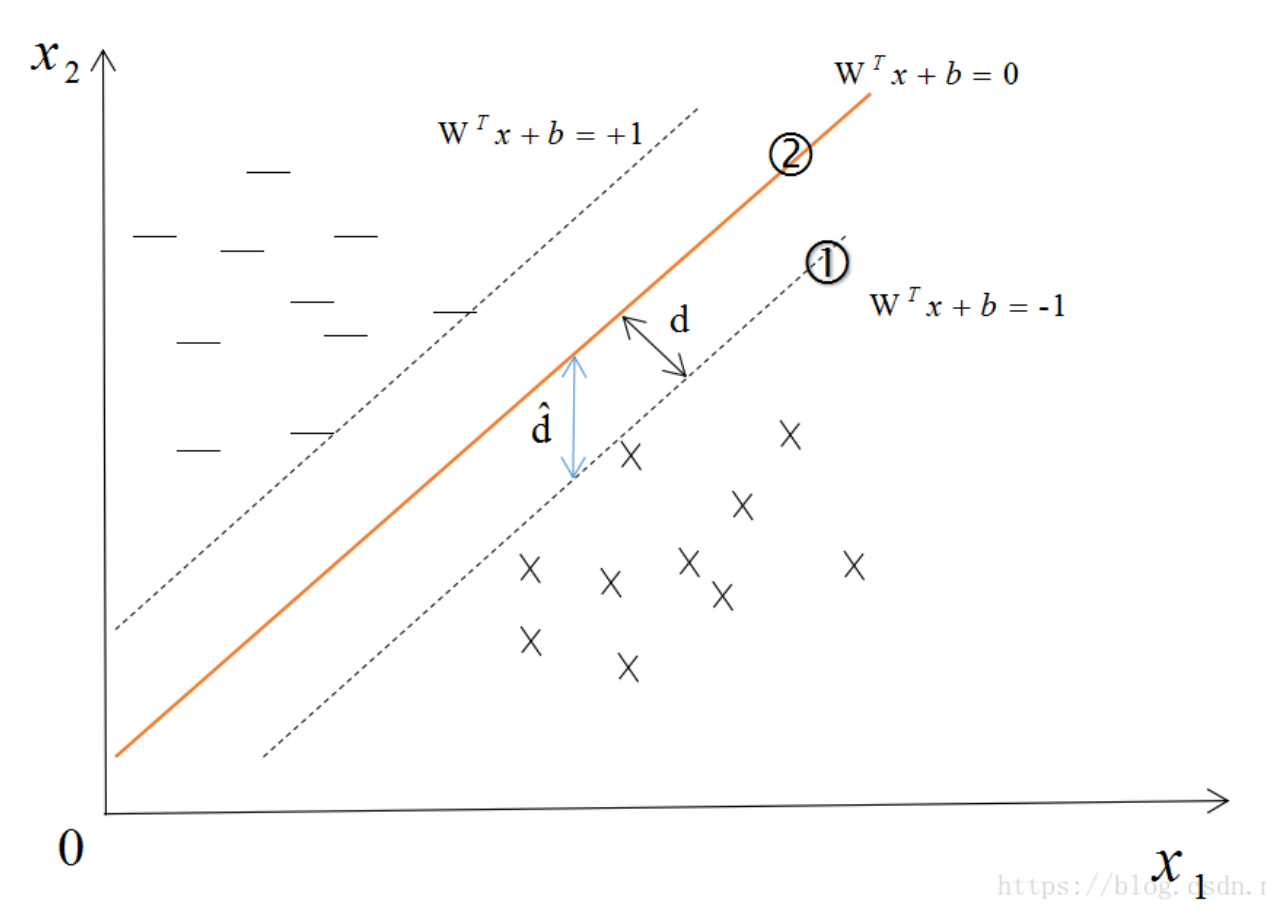
$d$为几何间隔,$\hat d$为函数间隔。我们在SVM中说的间隔指的是函数间隔。在实际应用中,有一些样本点可能并不满足最大间隔的限制:
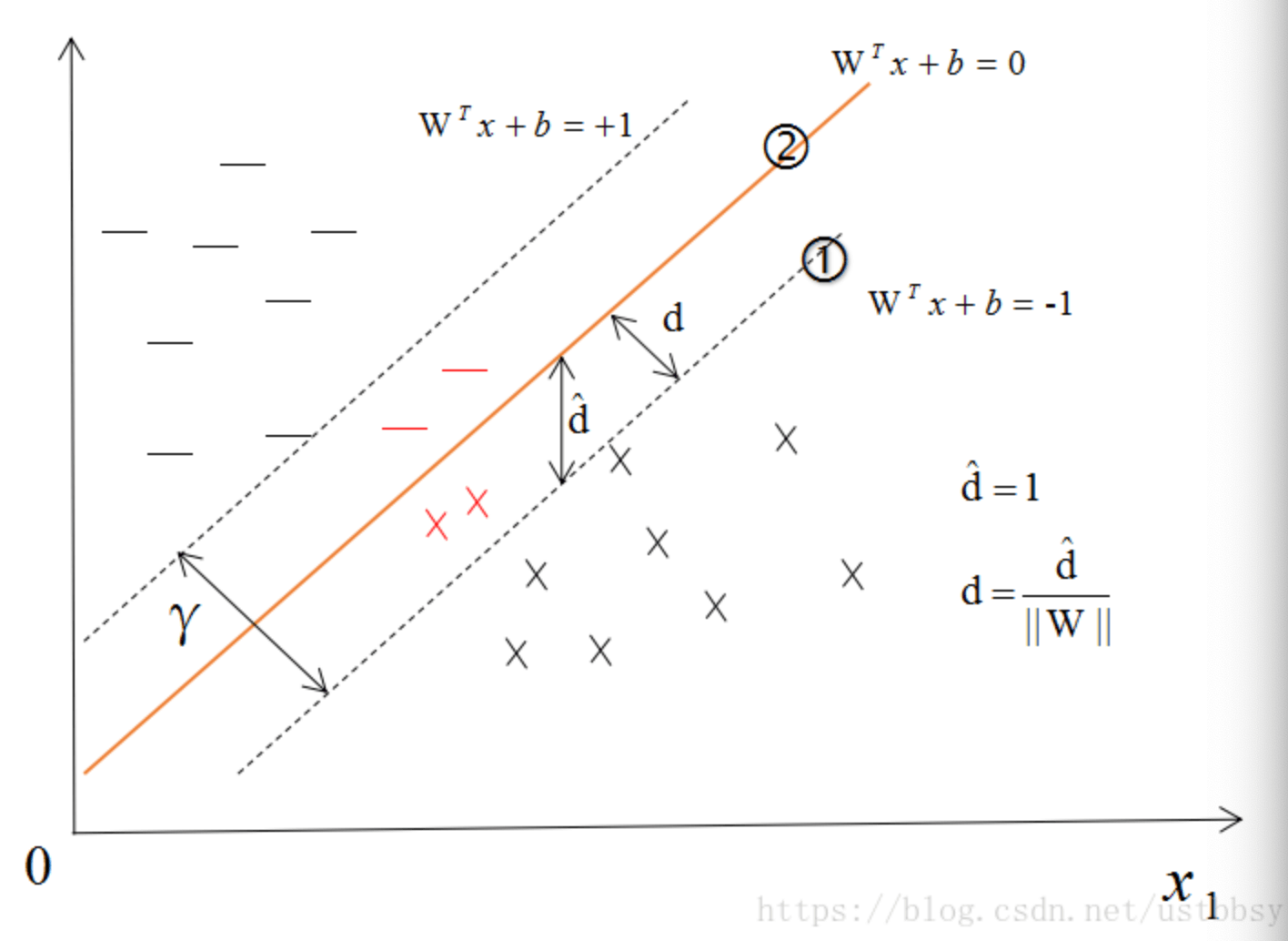
此时,我们便引入松弛变量来放松这些限制,使其可以在更大的一个范围内进行求解:

即第1部分的式(10)。