本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Laplace算子
Sobel算子属于一阶微分算子,利用了一阶导数,图像在边缘处的一阶导数值最大。而Laplace算子属于二阶微分算子,利用了二阶导数,图像在边缘处的二阶导数为零:
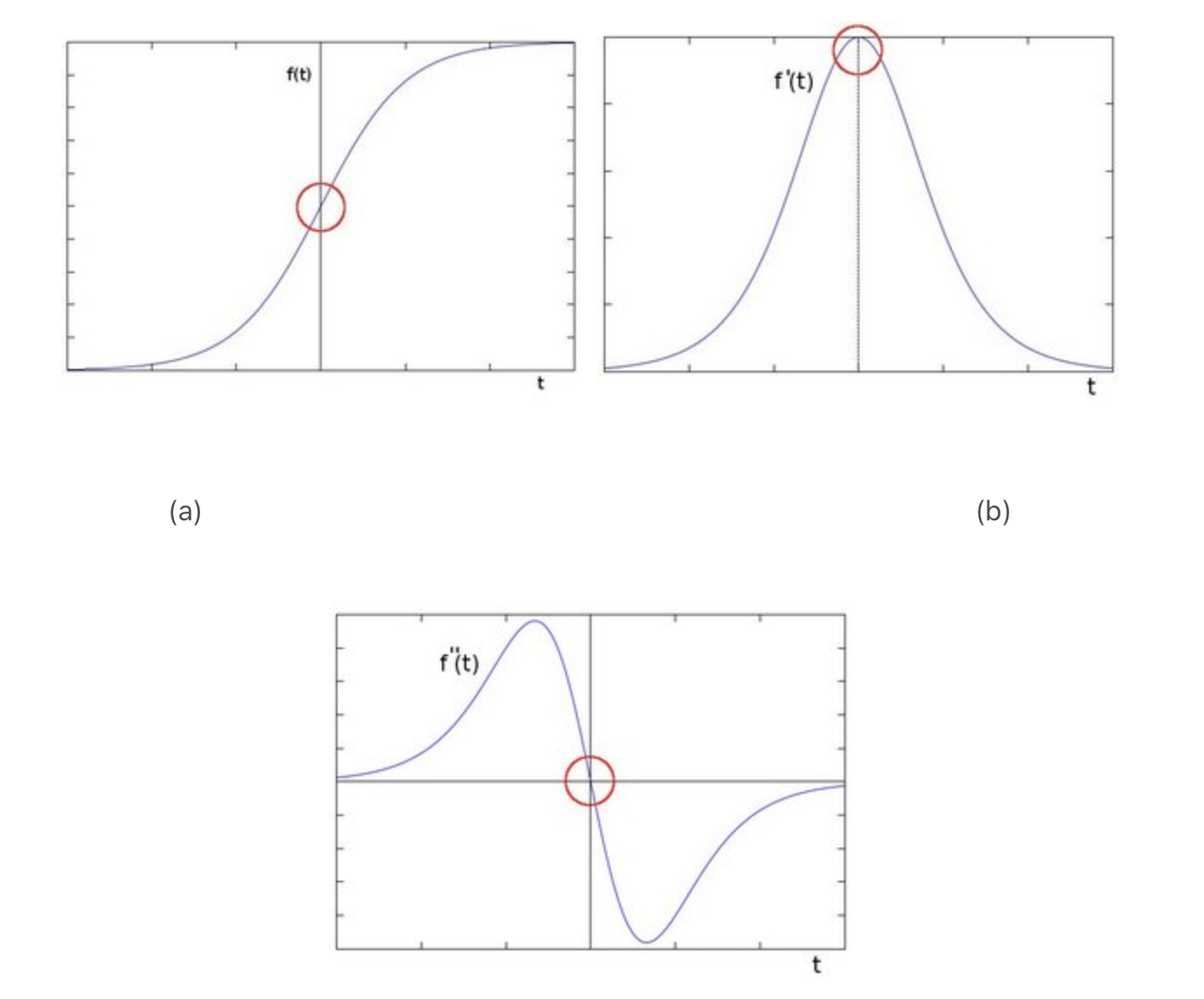
离散函数的导数退化成了差分,一维一阶差分公式和二阶差分公式分别为:
\[\frac{\partial f }{\partial x}=f'(x)=f(x+1)-f(x)\] \[\frac{\partial ^2 f }{\partial x^2}=f''(x)=f'(x)-f'(x-1)=f(x+1)+f(x-1)-2f(x)\]上述是一维情况下,那么在二维函数$f(x,y)$中,$x,y$两个方向的二阶差分分别为:
\[\frac{\partial ^2 f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)\] \[\frac{\partial ^2 f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y)\]所以Laplace算子的差分形式为:
\[\nabla ^2 f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)\]写成filter的形式:
\[\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \\ \end{bmatrix}\]如果把对角线方向也算上,则filter的形式可扩展为:
\[\begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \\ \end{bmatrix}\]2.API
1
2
3
4
5
6
7
8
9
void Laplacian(
InputArray src,
OutputArray dst,
int ddepth,
int ksize = 1,
double scale = 1,
double delta = 0,
int borderType = BORDER_DEFAULT
);
参数解释:
InputArray src:输入图片。OutputArray dst:输出图片。int ddepth:输出图片的位图深度。int ksize:filter大小,必须为正奇数。double scale:filter中的每一个值乘以scale。double delta:filter中的每一个值加上delta。int borderType:边界处理方式。
3.图像处理步骤
- 高斯模糊(去噪声):
GaussianBlur()。 - 转化为灰度图像:
cvtColor()。 - 应用Laplace算子:
Laplacian()。 - 图像取绝对值:
convertScaleAbs()。 - 显示结果。
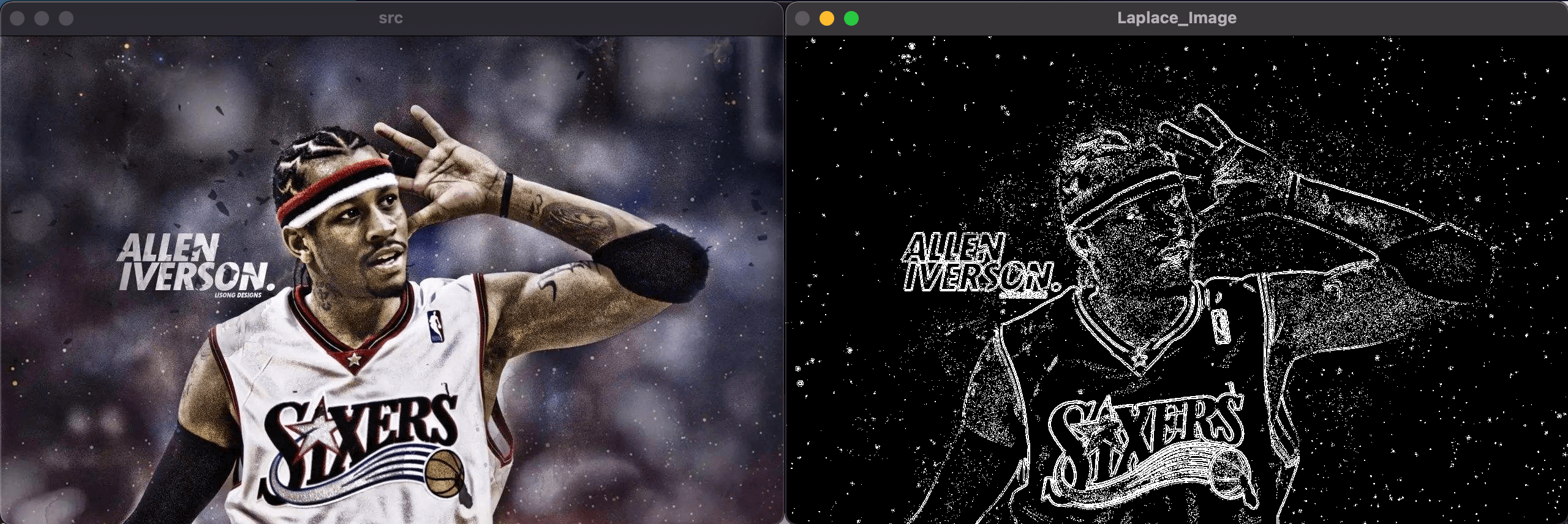
下左为原图,下右为应用Laplace算子的效果:
3.1.convertScaleAbs
1
2
3
4
5
6
void convertScaleAbs(
InputArray src,
OutputArray dst,
double alpha = 1,
double beta = 0
);
cv::convertScaleAbs()对整个图像数组中的每一个元素进行如下操作: