本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.霍夫变换
霍夫变换(Hough Transform)是一种特征提取手段,用来提取形状(直线、圆等)边界。
⚠️前提:霍夫变换检测边缘只对边缘图片(经过canny或者sobe算子提取特征后的图片)有效,对一般的图片无效。
2.霍夫变换-直线检测
2.1.笛卡尔坐标霍夫空间
在笛卡尔坐标系中,一条直线可由两个点$A=(x_1,y_1)$和$B=(x_2,y_2)$确定:

另一方面,$y=kx+q$也可以写成关于$(k,q)$的函数表达式:
\[\left\{ \begin{array}{c} q=-kx_1+y_1 \\ q=-kx_2+y_2 \end{array} \right.\]这个$(k,q)$空间就是霍夫空间。$(x,y)$坐标系中的一条直线,对应$(k,q)$霍夫空间的一个点:

反过来同样成立,$(k,q)$霍夫空间的一条直线,对应$(x,y)$坐标系的一个点:
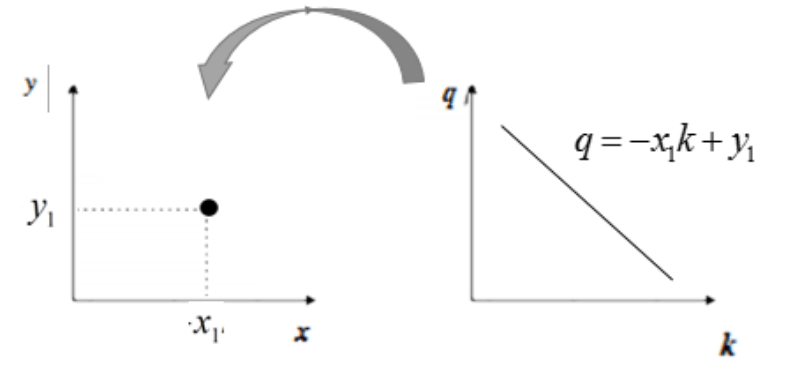
$(x,y)$坐标系中$A,B$两个点对应到$(k,q)$霍夫空间:
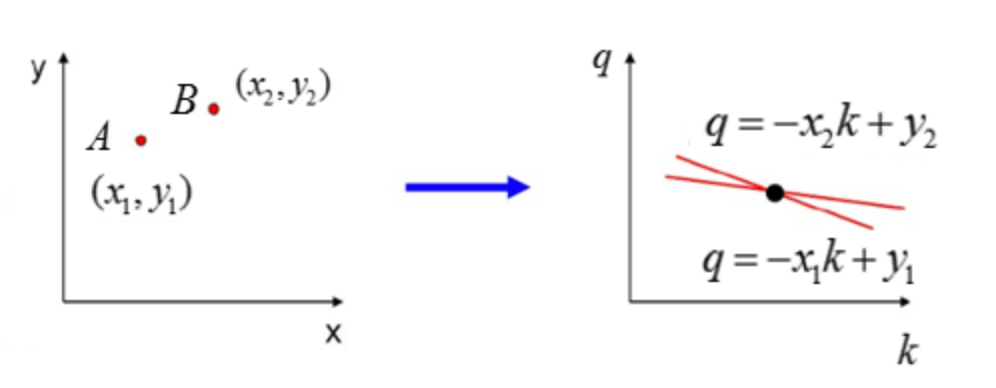
其中$(k,q)$霍夫空间中两条线的交点就是$(x,y)$坐标系中$A,B$两点确定的直线。更复杂的情况:
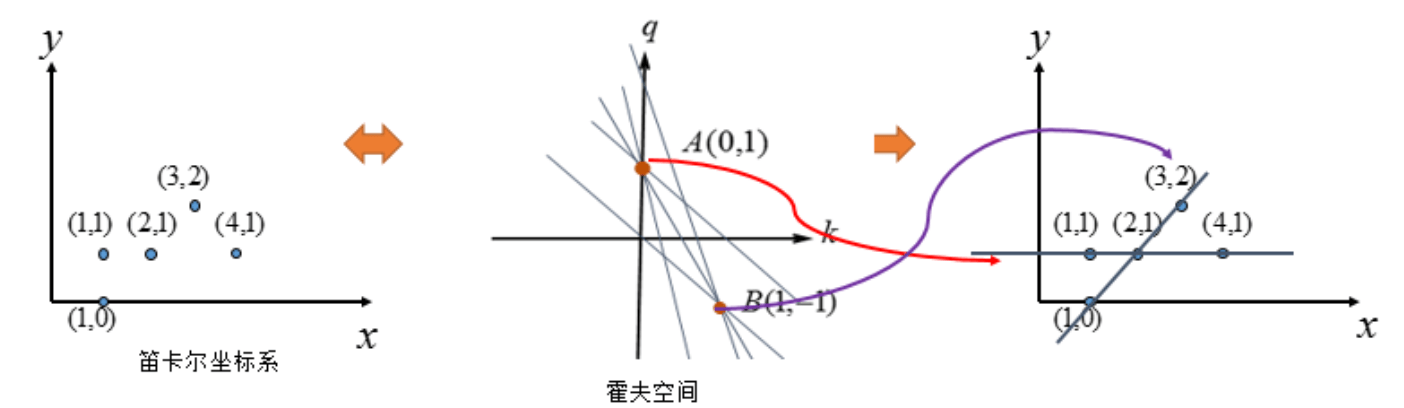
假设在$(x,y)$坐标系中,有三个点$(p_1,p_2,p_3)$共线,这三个点在$(k,q)$霍夫空间中对应着三条直线且这三条直线相交于一点。这是为什么呢?大家都知道两点可以确定一条直线,那么$p_1,p_2,p_3$就可以确定$C_3^2=3$条直线:$(p_1,p_2),(p_2,p_3),(p_1,p_3)$,又因为这三点是共线的,所以$(p_1,p_2),(p_2,p_3),(p_1,p_3)$这三条直线的$k,b$是一样的,即在$(k,q)$霍夫空间有相同的交点。反过来说,在$(k,q)$霍夫空间中,如果有一点$(k_g,q_g)$,穿过该点的直线有很多条,那么就意味着在$(x,y)$坐标系中有很多点是共线的,并且这条线的方程为$y=k_gx+q_g$。因此,我们便可以根据这个性质来对边缘图像的直线特征进行提取。
首先,将原图的$(x,y)$坐标系转换成$(k,q)$霍夫空间,然后我们遍历$(k,q)$霍夫空间的每一个点(可以设置不一样的步长,例如初始值均为0,$k$方向的步长为1,$q$方向的步长为2等)。统计每个点被直线穿过的次数$v$,并从大到小排列。这里我们可以设置一个阈值$T$,将高于阈值($v>T$)的点挑选出来,这些点映射回$(x,y)$坐标系便是我们最后提取出来的直线特征。
但是如果是下面这种情况呢:
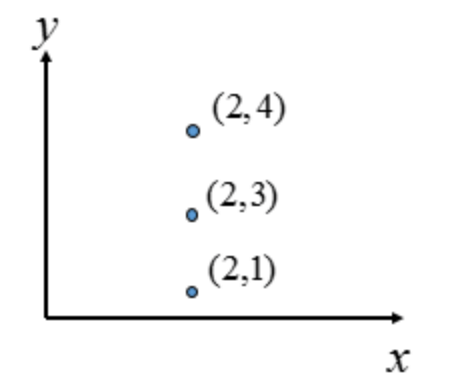
这三点所共同穿过的直线在$(k,q)$霍夫空间中无法很好的表示,因此提出了另一种更优的解决办法:极坐标霍夫空间。
2.2.极坐标霍夫空间
基本与2.1部分一样,唯一的不同之处在于将$(k,q)$霍夫空间改成了$(\rho,\theta)$极坐标霍夫空间:
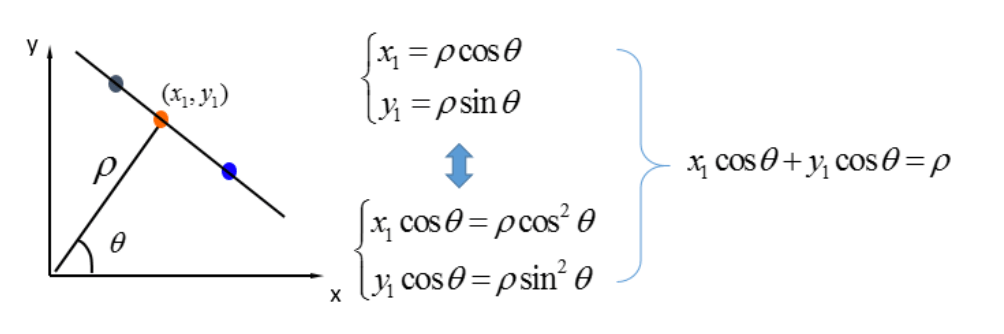
$\rho$为坐标原点到直线的垂直距离。$(x,y)$坐标系中的点转换到$(\rho,\theta)$极坐标霍夫空间不再是直线,而是正弦曲线:
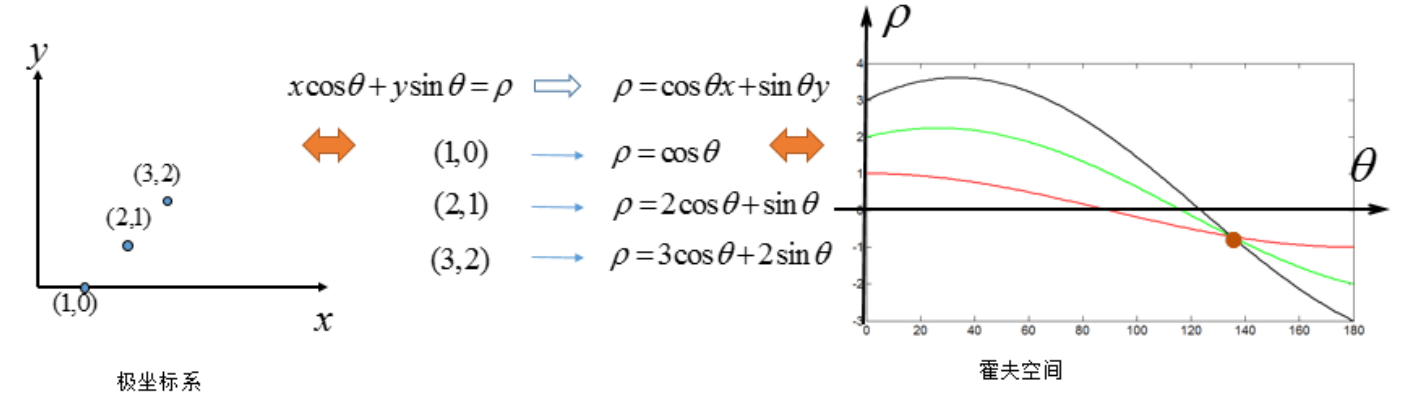
相应的,在遍历$(\rho,\theta)$极坐标霍夫空间时,可以通过设置不同的$\rho,\theta$值来控制步长。然后统计每个点被曲线穿过的次数。
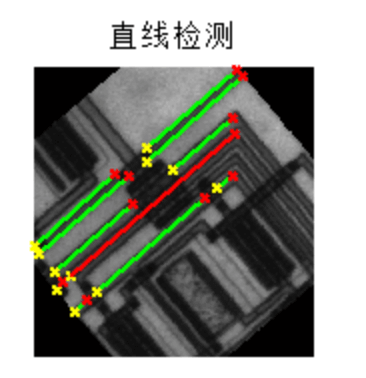
霍夫变换(直线检测)结果展示:
2.3.相关API
1
2
3
4
5
6
7
8
9
10
11
void HoughLines(
InputArray image,//输入图像,必须是8bit的灰度图像
OutputArray lines,//输出的极坐标来表示直线
double rho,//rho的步长,一般取1
double theta,//theta步长(弧度),一般取值为CV_PI/180,即1度
int threshold,//阈值T
double srn=0,//默认值为0。多尺度霍夫线变换才会用到的参数。对于多尺度霍夫线变换,rho轴的单位长度=rho/srn
double stn=0,//默认值为0。也是多尺度霍夫线变换才会用到的参数。对于多尺度霍夫线变换,theta轴的单位长度=theta/stn。如果srn、stn同时为0,就表示使用经典霍夫变换,否则两个参数都应该为正数
double min_theta=0,//theta取值范围
double max_theta=CV_PI//theta取值范围
);
弧度的定义是弧长比上半径,即为圆心角的弧度值,对于半径为1的圆,其周长为2$\pi$,所以对应的圆心角弧度值为2$\pi$,也就是一圈360度。在数学中所用到的角度,一般都用弧度表示,因为弧度对应的就是数轴上的实数,计算起来方便。还有在三角函数中用的也都是弧度值。
该API的输出结果为极坐标,需要用户自己转换回$(x,y)$坐标系。而下面这个API则可以直接输出$(x,y)$坐标系下直线的坐标,更推荐大家使用:
1
2
3
4
5
6
7
8
9
void HoughLinesP(
InputArray image,//输入图像,必须是8bit的灰度图像
OutputArray lines,//(x,y)坐标系下直线的坐标,由两个点坐标表示(x1,y1,x2,y2)
double rho,//rho的步长,一般取1
double theta,//theta步长(弧度),一般取值为CV_PI/180,即1度
int threshold,//阈值T
double minLineLength=0,//直线的最小长度
double maxLineGap=0//直线之间的最小距离
);
maxLineGap如果设置为5,则距离在5个像素以内的直线都被认为是同一条直线。
3.霍夫变换-圆检测
三个不共线的点可以确定一个圆。假设圆上一点的坐标为$(x,y)$,则圆的方程为$(x-a)^2+(y-b)^2=r^2$,$(a,b)$为圆心坐标,$r$为半径。类似于直线检测,将$(x,y)$坐标系转换到$(a,b)$坐标系。圆上的点$(x,y)$在霍夫空间是以$(x,y)$为圆心,$r$为半径的圆。在霍夫空间中,一个点$(m,n)$被多个圆(前提:相同的$r$)穿过,则说明这些圆在$(x,y)$坐标空间中对应的点是共圆的,且这个圆的圆心为$(m,n)$,半径为$r$。
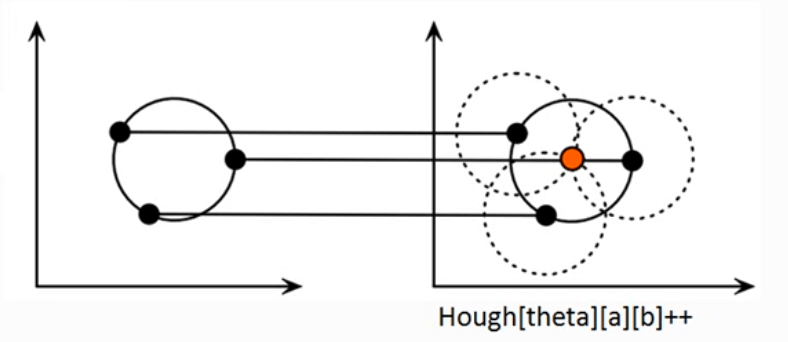
剩余的步骤和直线检测相同,不再赘述。
3.1.相关API
因为霍夫变换(圆检测)对噪声比较敏感,所以首先要对图像做中值滤波或高斯模糊。
基于效率考虑,OpenCV中实现的霍夫变换(圆检测)是基于图像梯度的实现,分为两步:
- 检测边缘,发现可能的圆心。
- 基于第一步的基础上从候选圆心开始计算最佳半径大小。
1
2
3
4
5
6
7
8
9
10
11
void HoughCircles(
InputArray image,
OutputArray circles,
int method,
double dp,
double minDist,
double param1 = 100,
double param2 = 100,
int minRadius = 0,
int maxRadius = 0
);
参数解释:
InputArray image:输入图像,需为8位的灰度单通道图像。OutputArray circles:输出vector,vector中的每个元素均包含$(x,y,radius)$。int method:检测方法,目前OpenCV中就霍夫梯度法(HOUGH_GRADIENT)一种可以使用。double dp:用来检测圆心的累加器图像的分辨率与输入图像之比的倒数,且此参数允许创建一个比输入图像分辨率低的累加器。例如,如果dp=1时,累加器和输入图像具有相同的分辨率。如果dp=2,累加器便有输入图像一半那么大的宽度和高度。double minDist:为霍夫变换(圆检测)检测到的圆的圆心之间的最小距离,即让算法能明显区分的两个不同圆之间的最小距离。这个参数如果太小的话,多个相邻的圆可能都被错误地检测成了一个重合的圆。反之,这个参数设置太大,某些圆就不能被检测出来。double param1:默认值为100。它是第三个参数method设置的检测方法的对应参数。对当前唯一的方法HOUGH_GRADIENT,它表示传递给canny边缘检测算子的高阈值,而低阈值为高阈值的一半。double param2:默认值为100。它是第三个参数method设置的检测方法的对应参数。对当前唯一的方法HOUGH_GRADIENT,它表示在检测阶段圆心的累加器阈值。它越小,就越可以检测到更多根本不存在的圆,而它越大的话,能通过检测的圆就更加接近完美的圆形了。int minRadius:默认值为0,表示圆半径的最小值。int maxRadius:默认值为0,表示圆半径的最大值。
该API内自带canny边缘检测,不需要再专门处理边缘。