本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.二叉树
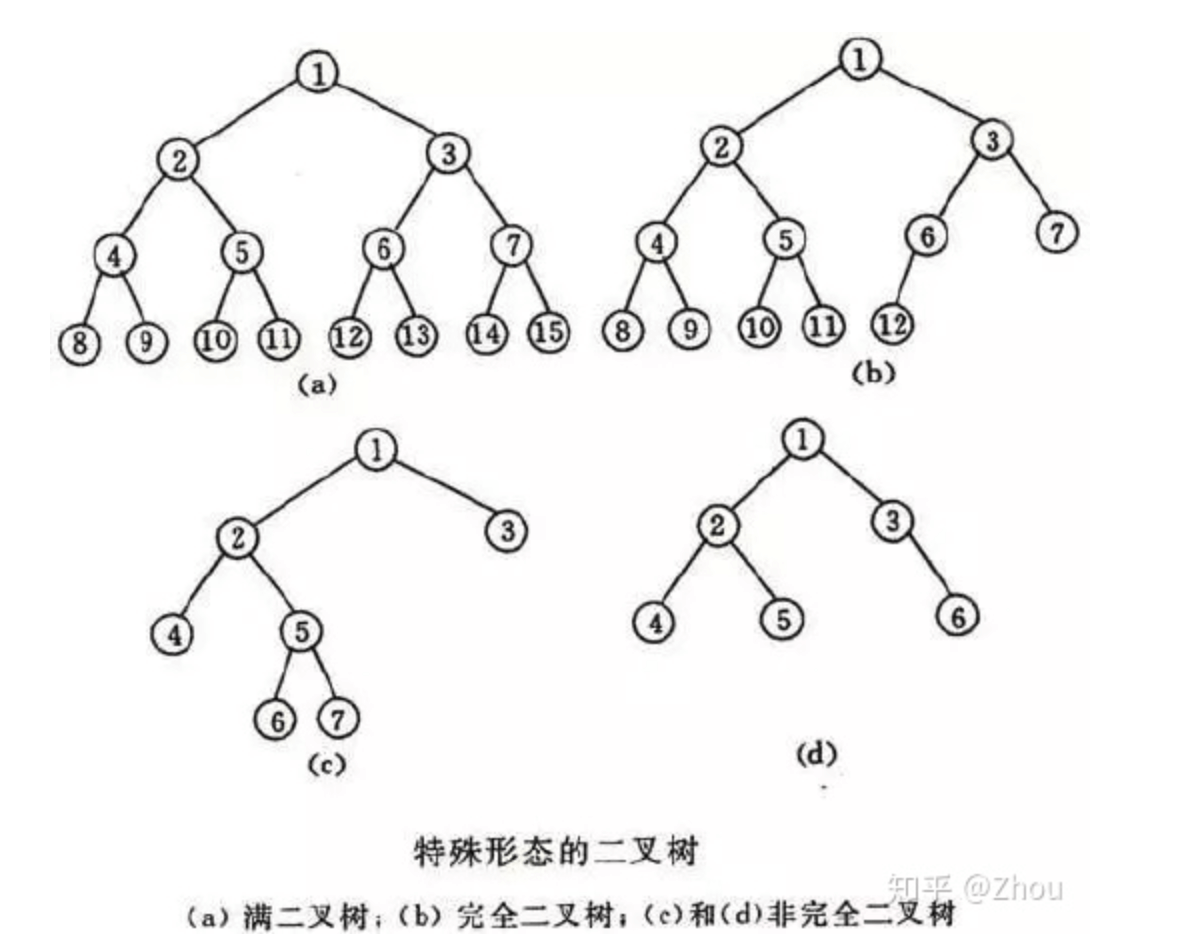
在计算机科学中,二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
👉一棵深度为$k$,且最底层有$2^{(k-1)}$个节点称之为满二叉树。
👉若设二叉树的深度为$h$,除第$h$层外,其它各层(1~h-1)的结点数都达到最大个数,第$h$层所有的结点都连续集中在最左边,这就是完全二叉树。
2.堆排序
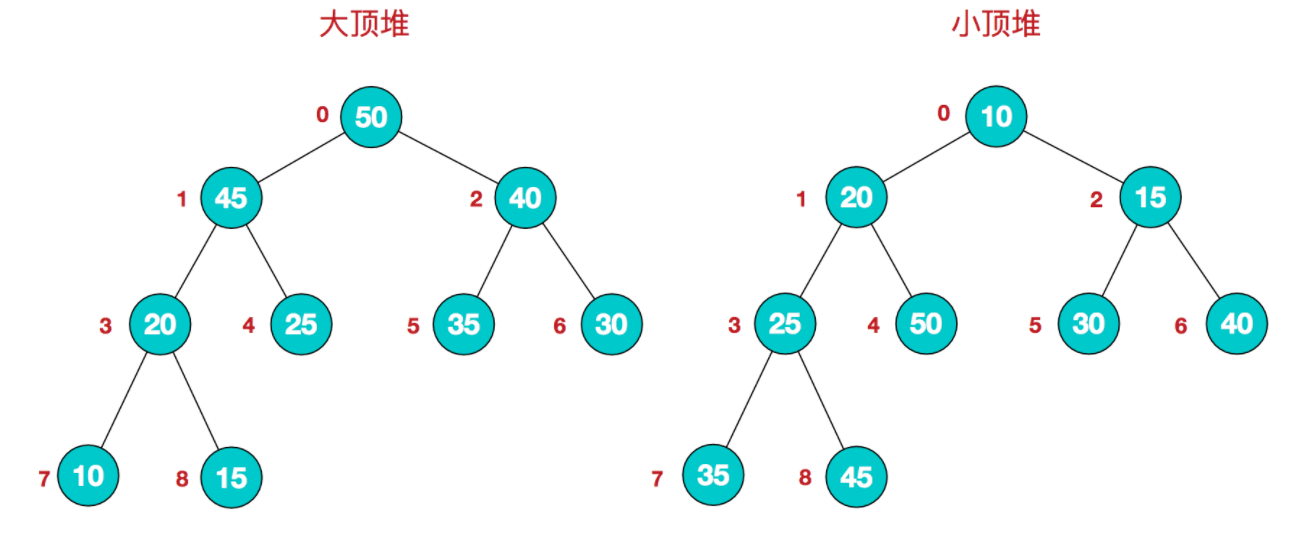
堆排序是利用堆这种数据结构而设计的一种排序算法。堆是具有以下性质的完全二叉树:每个父结点的值都大于或等于其左右子结点的值,称为大顶堆;或者每个父结点的值都小于或等于其左右子结点的值,称为小顶堆。如下图:
我们以待排序列[57,40,38,11,13,34,48,75,6,19,9,7]为例,使用大顶堆:
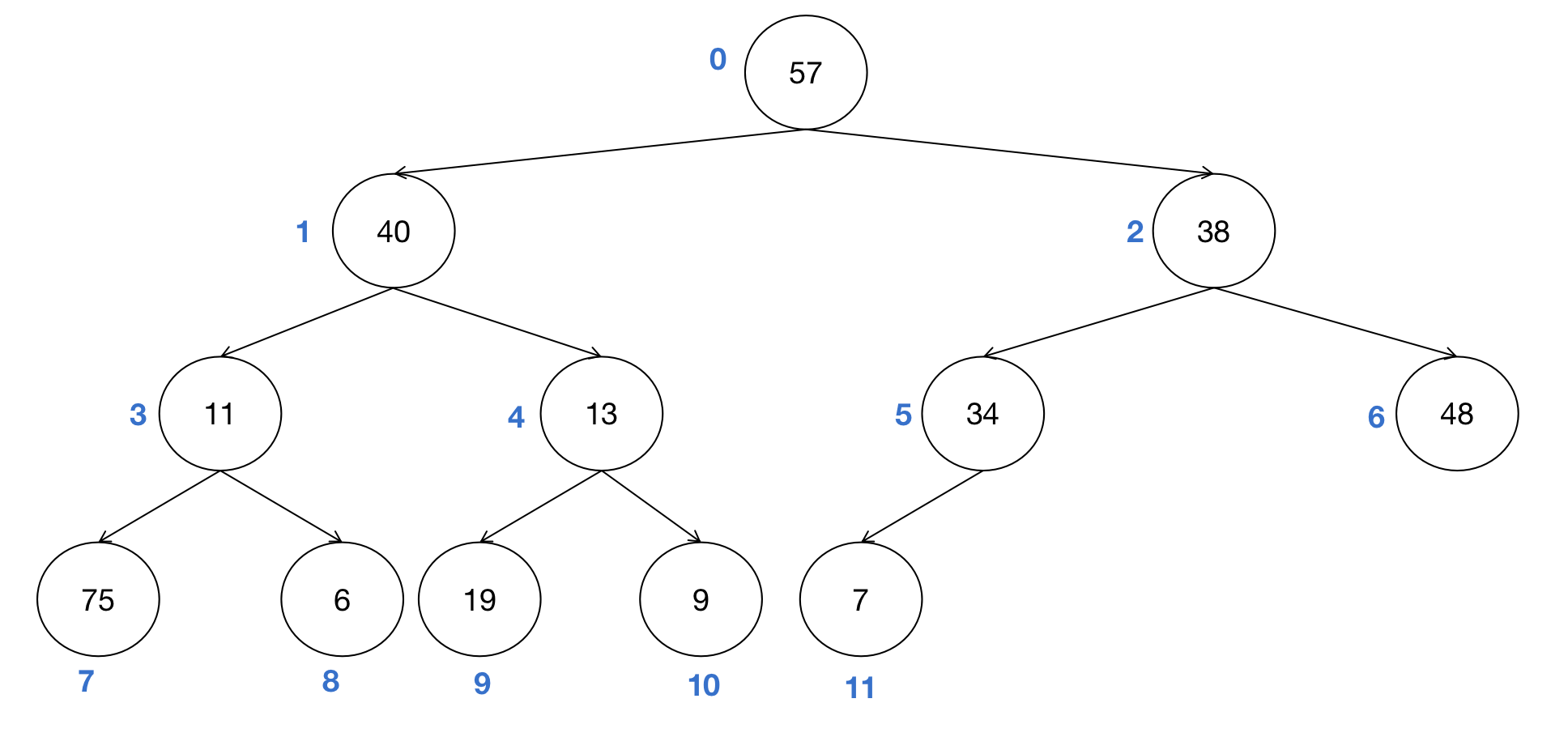
- 节点6(48)为叶子节点,不需要操作。
- 节点5(34)的子节点为7,不需要调换位置。
- 节点4(13)的子节点为19和9,需要调换13和19的位置。
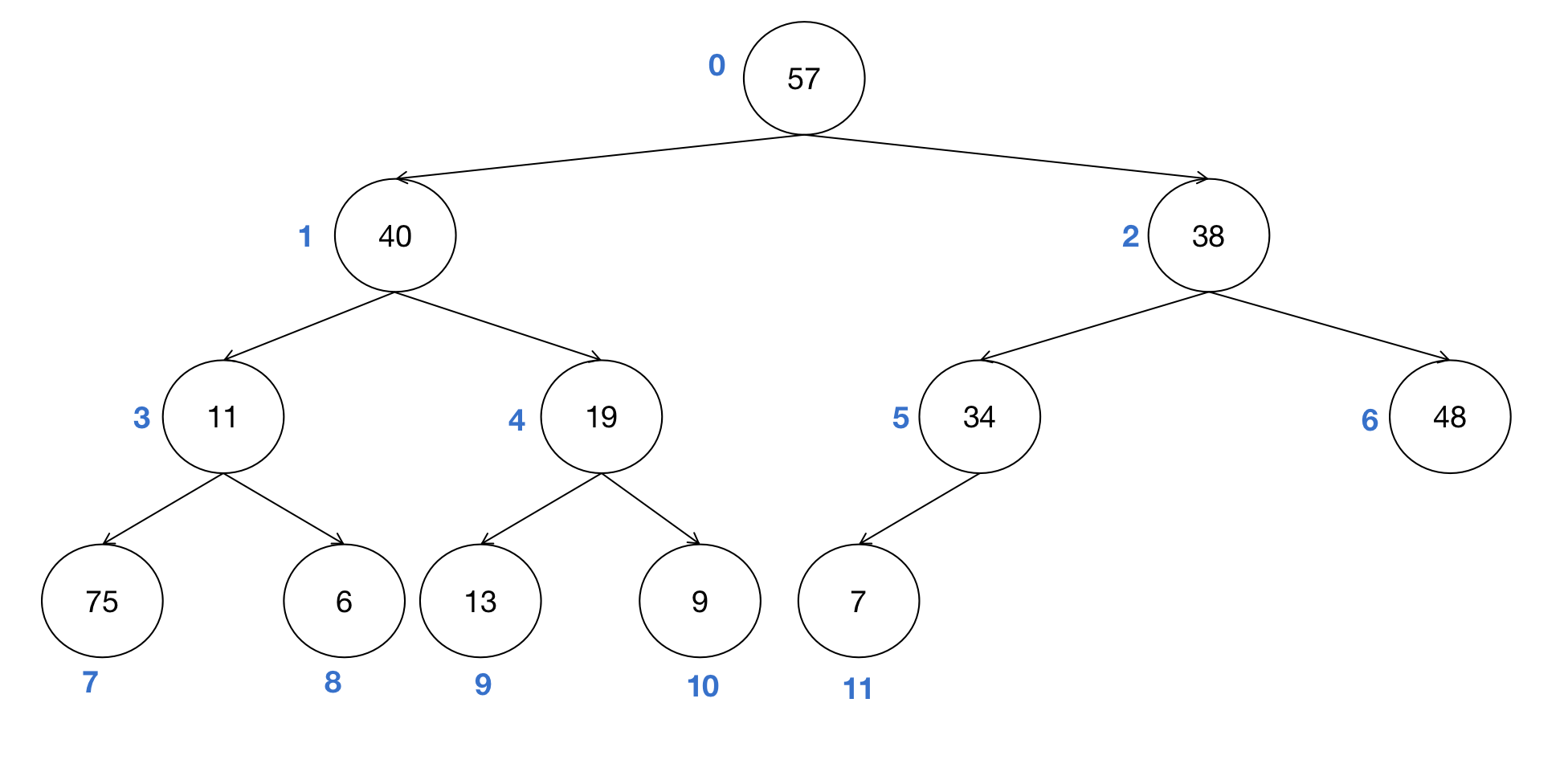
- 节点3(11)的子节点为75和6,需要调换11和75的位置。

- 节点2(38)的子节点为34和48,需要调换38和48的位置。

- 调换之后的节点6(38)为叶子节点,不需要操作。
- 节点1(40)的子节点为75和19,需要调换40和75的位置。
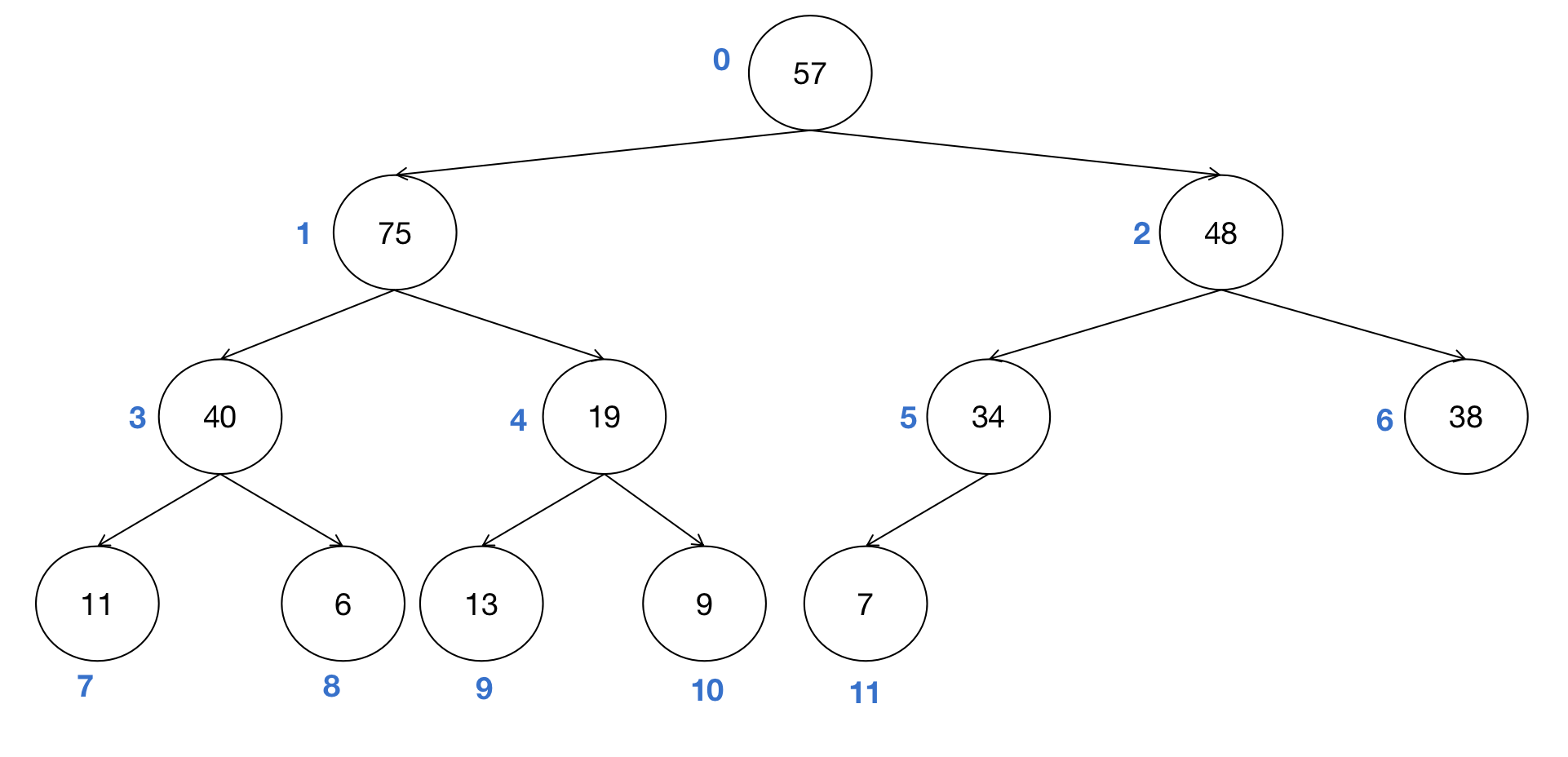
- 调换后的节点3(40)比其两个子节点的值(11和6)都大,因此不需要进一步调整。
- 节点0(57)的子节点为75和48,需要调换75和57的位置。
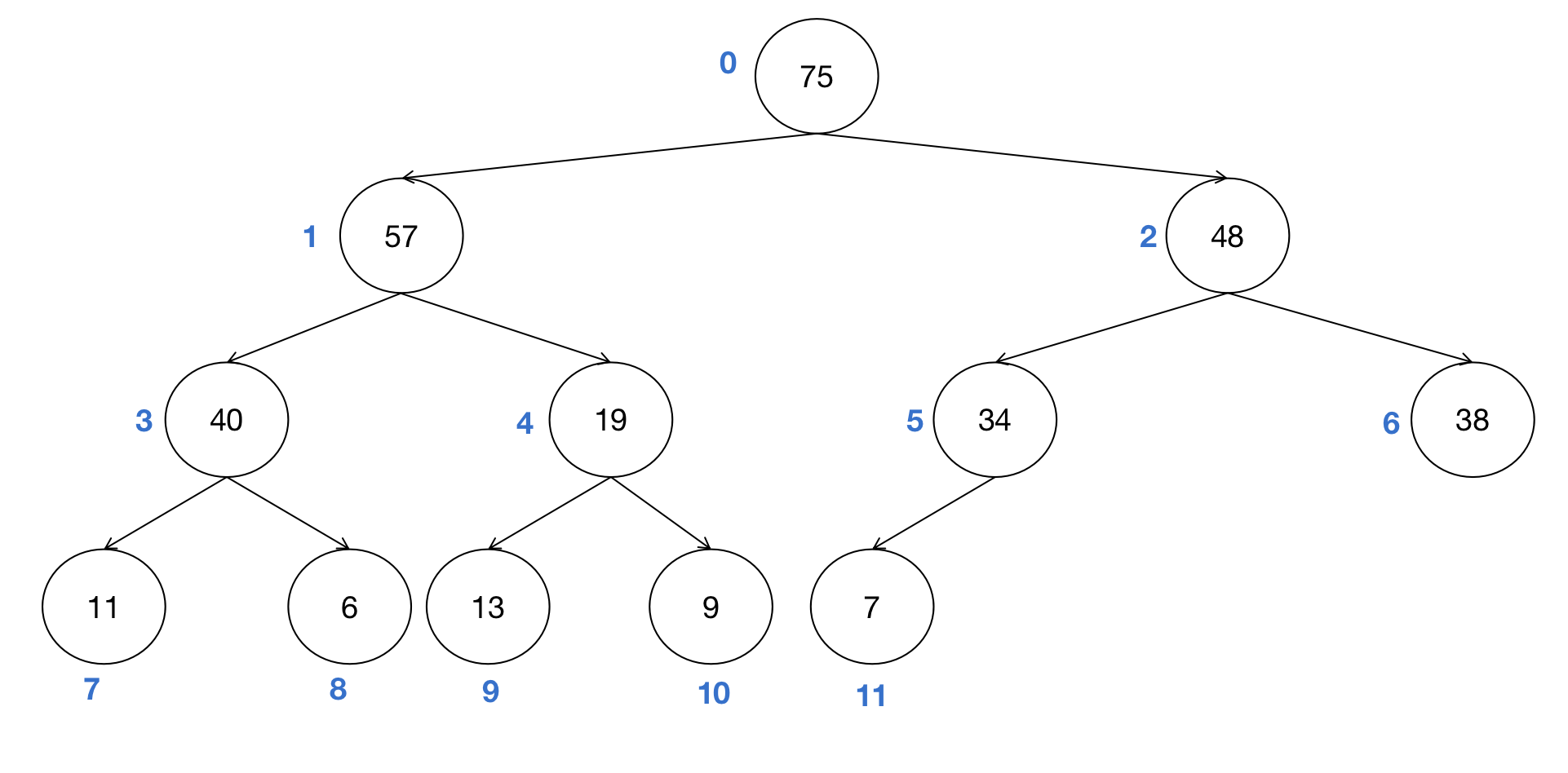
- 调换之后的节点1(57)比其两个子节点的值(40和19)都大,因此不需要进一步调整。
- 将75和最后一个节点(即节点11)调换位置。之后节点11(75)作为有序区,不再参与后续迭代,排除在树形结构之外。

- 待排序列变为
[7,57,48,40,19,34,38,11,6,13,9,75]。 - 由堆的根节点(节点0)开始调整,与其大孩子交换,逐层向下,使重新成堆。
- 节点0(7)与其大孩子(节点1(57))交换位置。
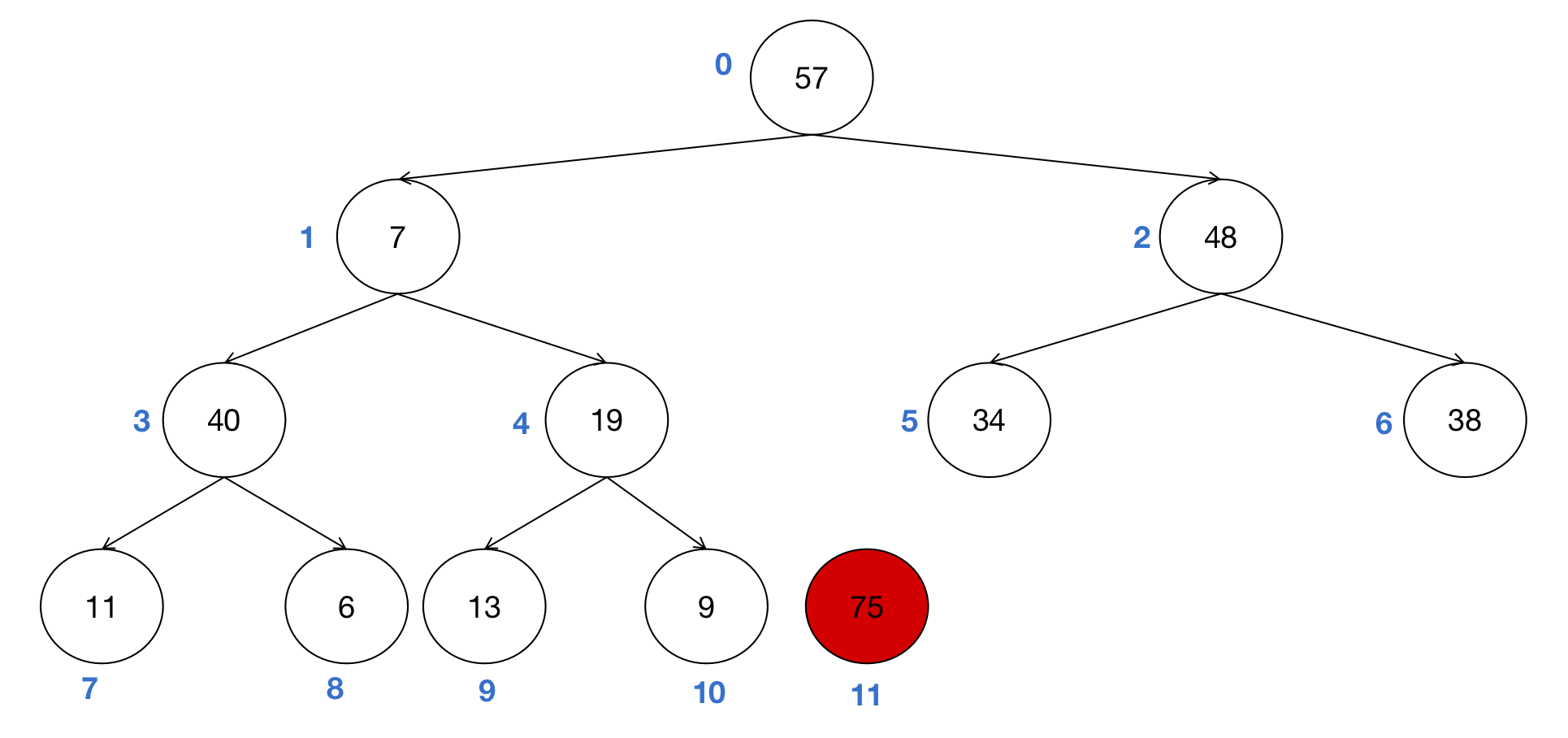
- 继续调整7(节点1)的位置,将其与其大孩子(节点3(40))交换位置。

- 继续调整7(节点3)的位置,将其与其大孩子(节点7(11))交换位置。

- 将根节点(57)和最后一个节点(即节点10(9))交换位置。之后节点10(57)也进入有序区,被排除在树形结构之外。
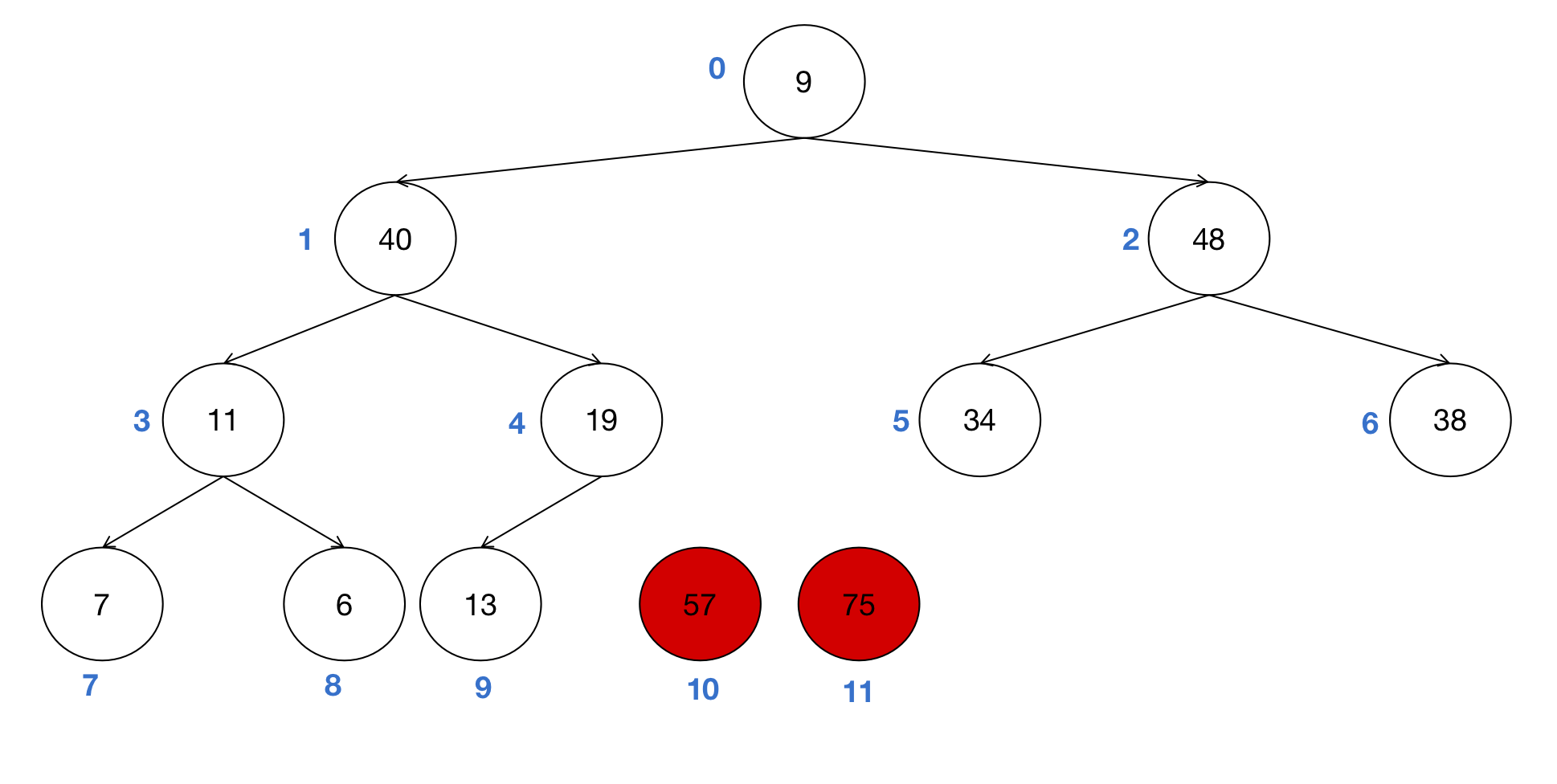
- 待排序列变为
[9,40,48,11,19,34,38,7,6,13,57,75]。 - 重新从堆的根节点进行调整。节点0(9)与其大孩子(节点2(48))交换位置。

- 继续调整节点2(9)的位置,将其与其大孩子(节点6(38))交换位置。
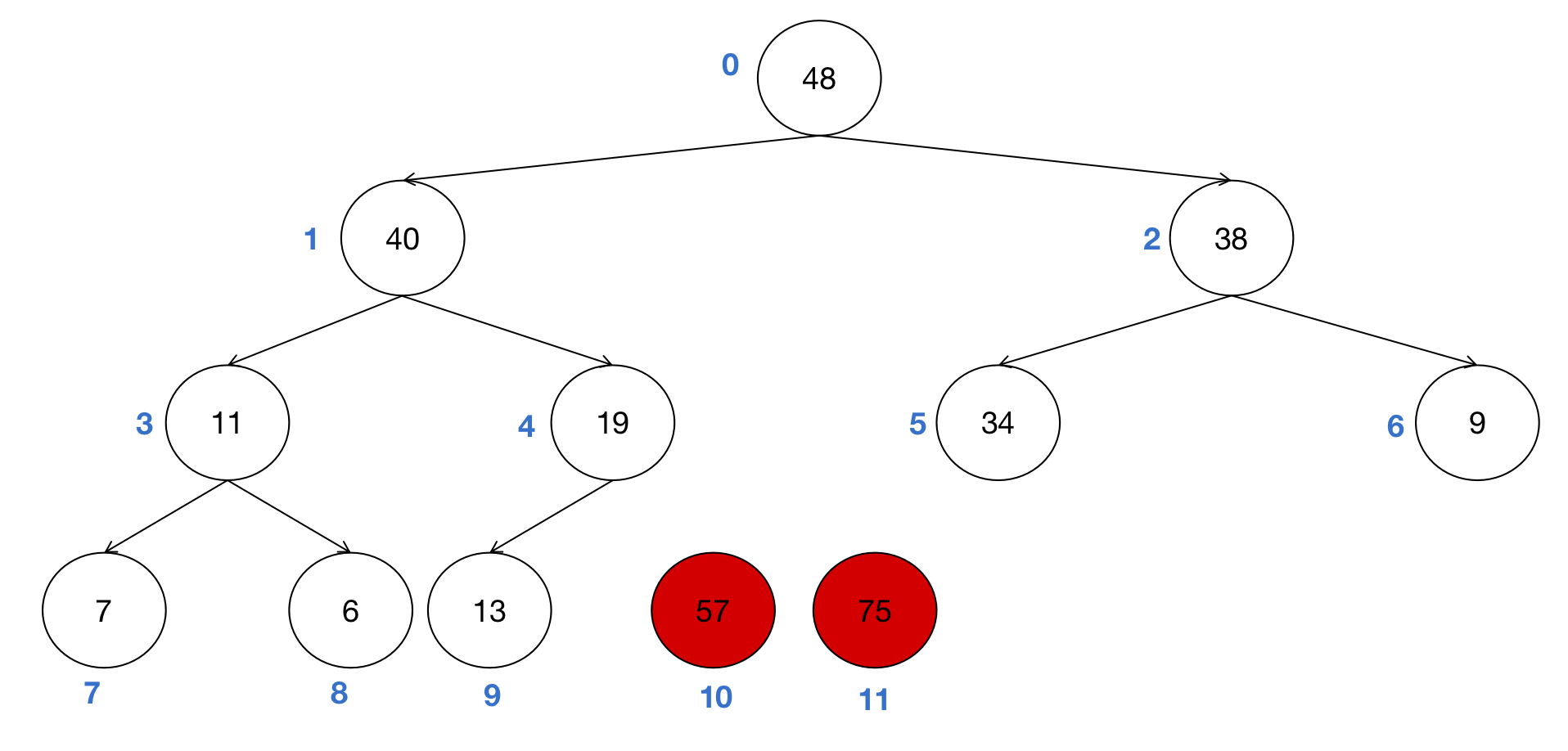
- 将根节点(48)和最后一个节点(即节点9(13))交换位置。之后节点9(48)也进入有序区,被排除在树形结构之外。

- 待排序列变为
[13,40,38,11,19,34,9,7,6,48,57,75]。
这个迭代一直持续到最后一个元素即完成堆排序步骤。