本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.使用sklearn建立决策树
1
2
3
4
5
6
7
8
9
from sklearn.datasets import load_iris
from sklearn import tree
iris = load_iris()
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)
# 产生预测结果
predicted = clf.predict(iris.data)
DecisionTreeClassifier中部分参数解释:
criterion:决策树划分标准。默认为“gini”。max_depth:限制树的深度。
iris数据集概览print(iris.DESCR):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
Iris Plants Database
====================
Notes
-----
Data Set Characteristics:
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
This is a copy of UCI ML iris datasets.
http://archive.ics.uci.edu/ml/datasets/Iris
The famous Iris database, first used by Sir R.A Fisher
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
References
----------
- Fisher,R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
2.将分类结果显示在图上
1
2
3
4
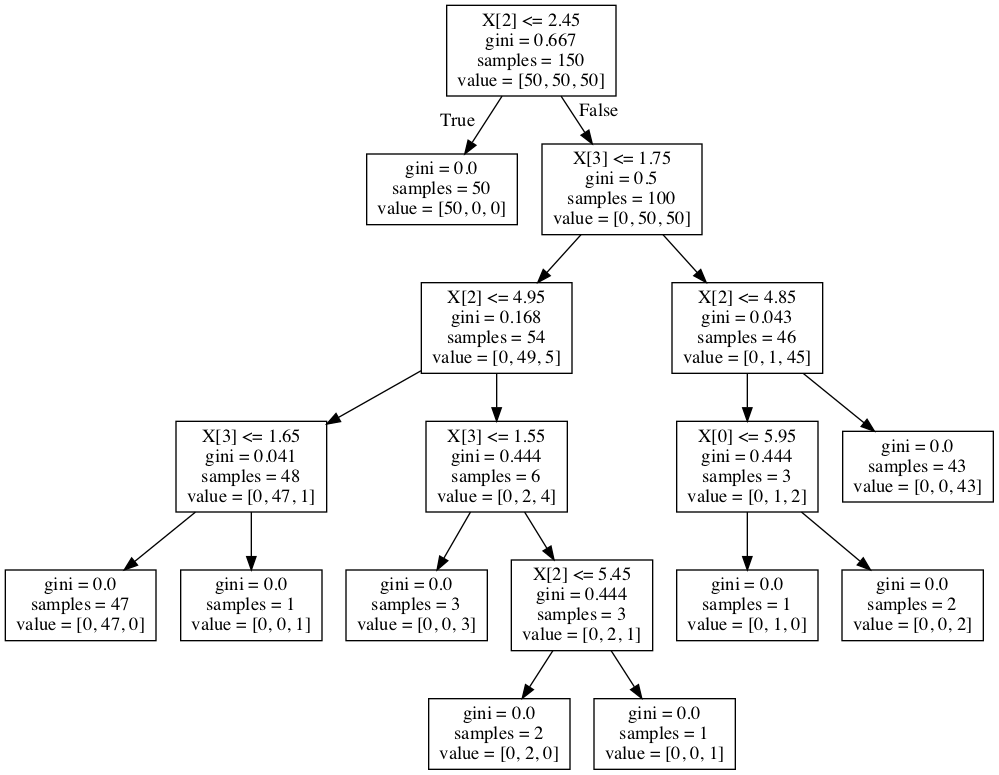
# 绘制成树形图
from sklearn import tree
tree.export_graphviz(clf, out_file='tree.dot')
使用graphviz读取dot文件并将其转换为png图像进行可视化:dot -Tpng tree.dot -o tree.png。也可转换成svg格式:dot -Tsvg tree.dot -o tree.svg。
graphviz官网:http://www.graphviz.org。
Mac推荐使用homebrew下载graphviz:
brew install graphviz。
3.建立决策边界
首先和第1部分一样,构建决策树分类模型:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn import tree
iris = load_iris()
X = iris.data[:, [2, 3]]#只使用两个变量
y = iris.target
clf = tree.DecisionTreeClassifier(max_depth=2)
clf.fit(X, y)
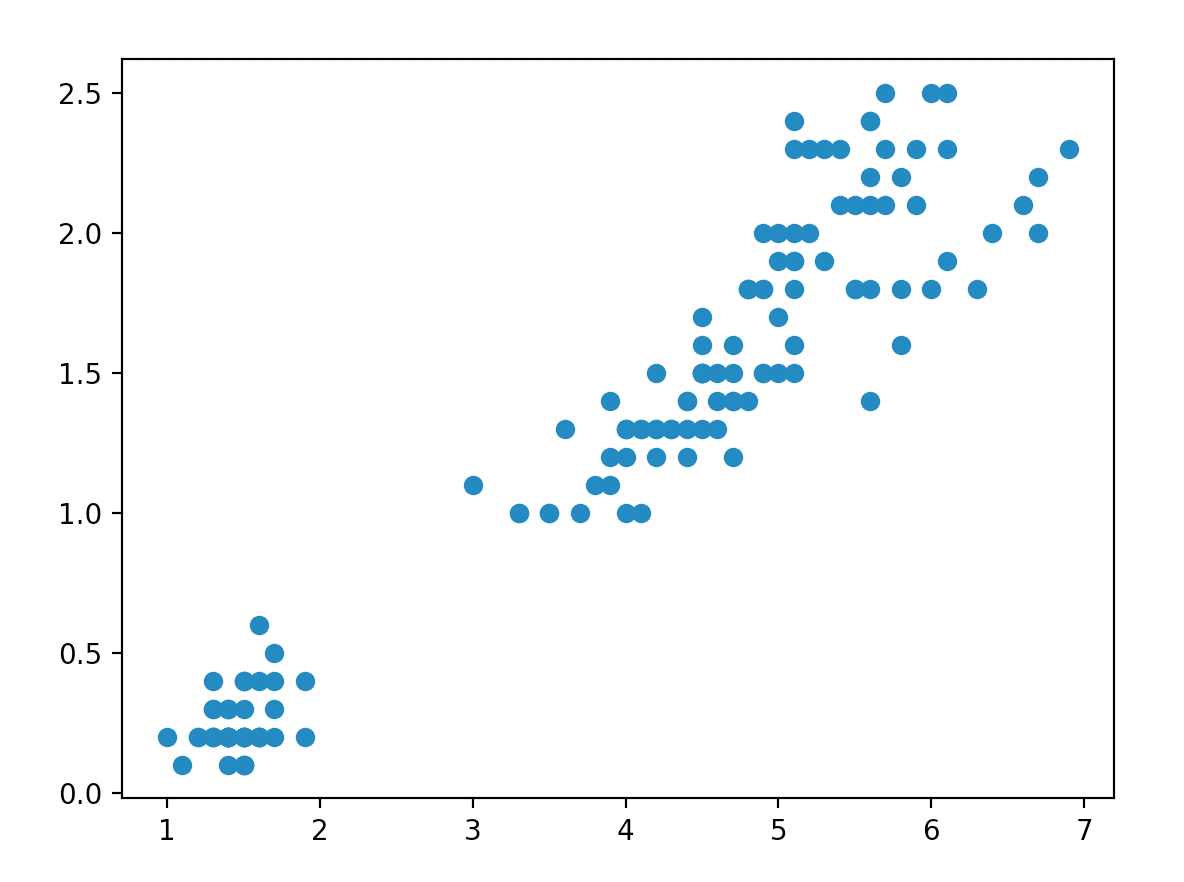
看下X这两个变量的分布情况:
1
2
3
plt.plot()
plt.scatter(X[:, 0], X[:, 1])
plt.show()
绘制决策边界:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
plt.plot()
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
#参数alpha为透明度
#参数cmap为colormap
plt.contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.rainbow)
#参数c为颜色
#参数alpha为透明度
#参数cmap为colormap
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=1, cmap=plt.cm.YlOrRd)
plt.title('Decision Tree')
plt.xlabel('Petal.Length')
plt.ylabel('Petal.Width')
plt.show()
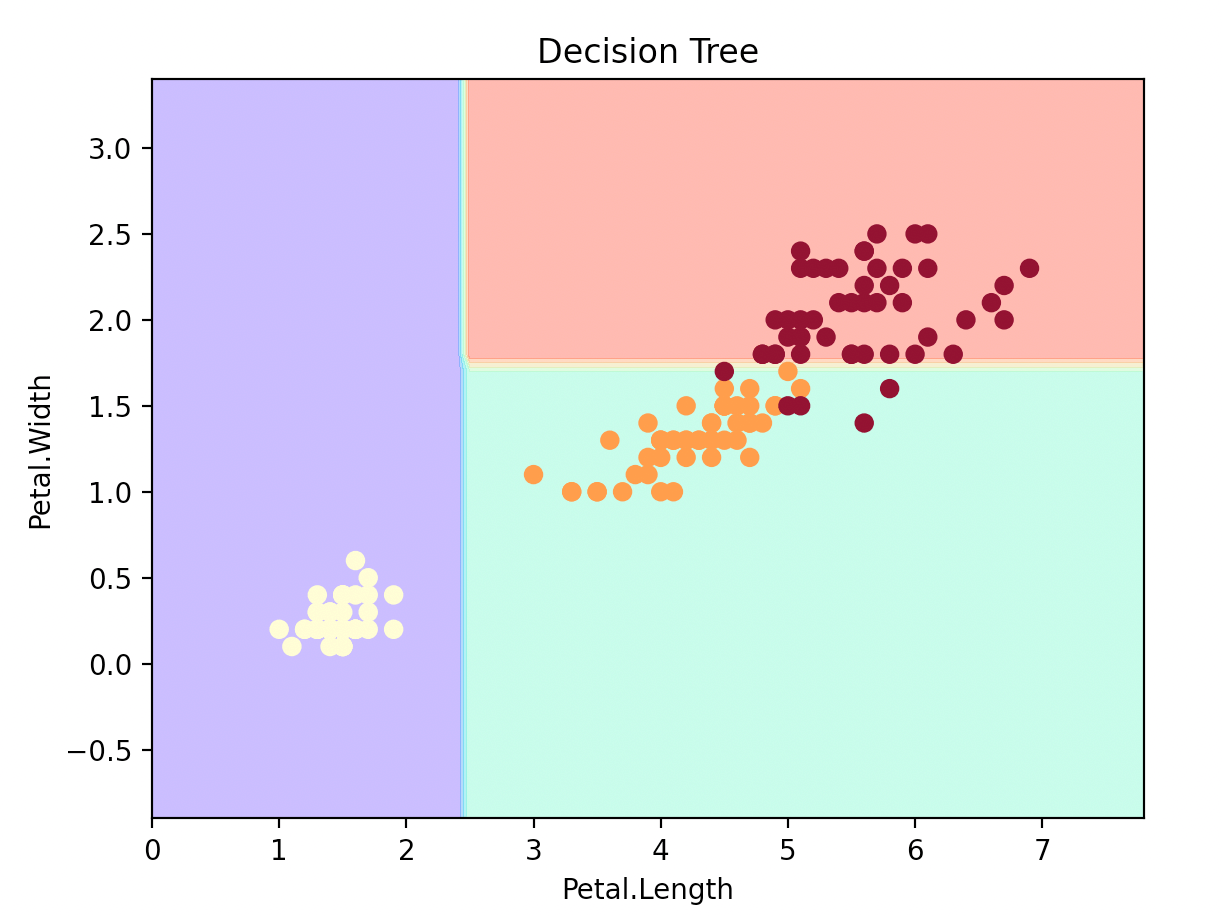
每种底色代表一个类别标签。底色通过plt.contourf绘制。
3.1.numpy.arange
numpy.arange(start,stop,step):
1
2
3
np.arange(0,1,0.2)
#输出为:
#array([0. , 0.2, 0.4, 0.6, 0.8])
3.2.numpy.meshgrid
1
xx,yy=np.meshgrid(np.arange(0,1,0.2),np.arange(1,3,1))
xx为:
1
2
array([[0. , 0.2, 0.4, 0.6, 0.8],
[0. , 0.2, 0.4, 0.6, 0.8]])
yy为:
1
2
array([[1, 1, 1, 1, 1],
[2, 2, 2, 2, 2]])
3.3.ravel
1
a = np.arange(12).reshape(3,4)
a为:
1
2
3
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
a.ravel()为扁平化操作:
1
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
和a.flatten()的结果是一样的。
3.4.numpy.c_
numpy.c_为按列连接两个矩阵。numpy.r_为按行连接两个矩阵。
1
2
3
4
#1
np.c_[np.array([1,2,3]), np.array([4,5,6])]
#2
np.r_[np.array([1,2,3]), np.array([4,5,6])]
1
2
3
4
5
6
#1
array([[1, 4],
[2, 5],
[3, 6]])
#2
array([1, 2, 3, 4, 5, 6])