本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
生成模型(the generative model)可以比喻成假币制造者,而与之对抗的判别模型(the discriminative model)可以看作是假币鉴定者,二者互项博弈,促进对方改进自己的假币制造技术或鉴别水平,直至假币制造者所制造的假币和真币无法区分。这便是GAN(Generative Adversarial Nets)的核心思想。
在本文中,我们讨论了生成模型和判别模型都是多层感知器(a multilayer perceptron,可理解为人工神经网络)的特殊情况。我们称这种特殊情况(this special case)为对抗网络(adversarial nets)。这就使得深度生成模型(deep generative models)可以利用人工神经网络的一些优良特性(例如反向传播算法和dropout),且不再需要近似推理和马尔科夫链。
论文中给出了代码地址:https://github.com/goodfeli/adversarial。
2.Related work
列举了一些相关方法及其缺点,不再详述。
3.Adversarial nets
构建生成网络$G(\mathbf z;\theta_g)$,其中,$\mathbf z$为网络G的输入(具有先验信息的噪声图像),$\theta_g$为网络G的参数,网络G的输出为假的样本图像。其次还需构建判别网络$D(\mathbf x;\theta_d)$,其中,$\mathbf x$为网络D的输入(真实的样本图像或假的样本图像),$\theta_d$为网络D的参数,网络D的输出为$\mathbf x$属于真实样本图像的概率。 因此我们可以构建如下value function:
\[\min \limits_{G} \ \max \limits_{D} V(D,G) = \mathbb{E}_{\mathbf x \sim p_{data}(\mathbf x)} [\log D(\mathbf x)]+\mathbb{E}_{\mathbf z \sim p_{\mathbf z} (\mathbf z)} [\log (1-D(G(\mathbf z)))] \tag{1}\]也就是说在训练模型D时,我们应该最大化$V(D,G)$,而在训练模型G时,我们应该最小化$V(D,G)$。具体的公式解释和证明请见本文第4部分。
更直观的解释请见图1:
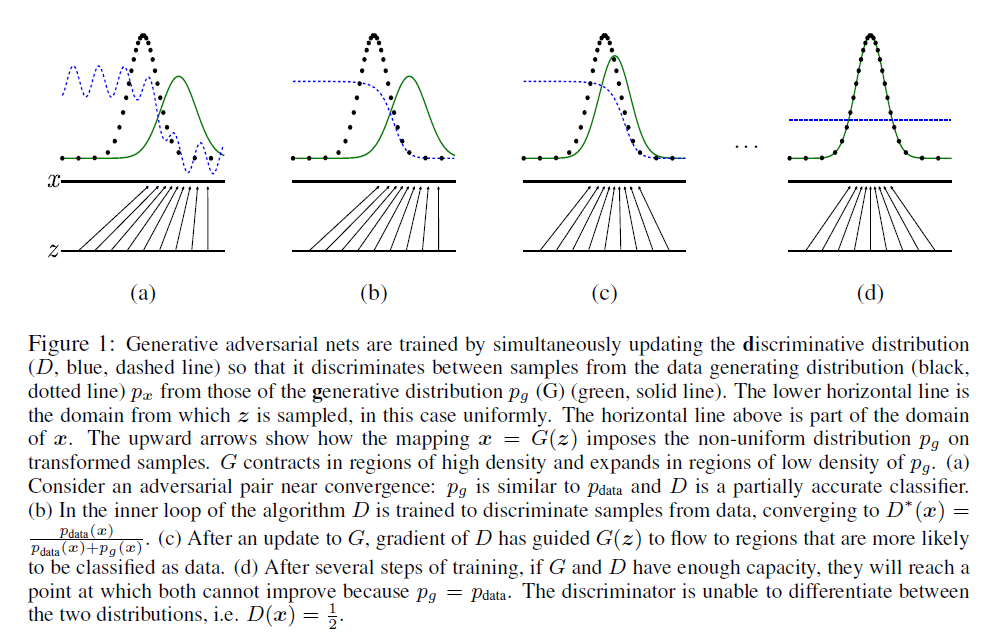
图1中,黑色点可理解为真实样本图像,绿色实线为假的样本图像,蓝色虚线为判别模型D。最下方的横线为噪声图像$\mathbf z$,上方的横线为样本$\mathbf x$(真实样本或生成样本),中间的箭头表示一种映射关系(可理解为生成模型G)。图1(a)构建了D和G,图1(b)首先优化了模型D,紧跟着图1(c)中优化了模型G,如此迭代,直至模型D无法区分真实数据和假数据,即$D(\mathbf x)=\frac{1}{2}$。
我们在优化模型D时不能总是用同样的数据集,这样容易造成过拟合。算法的详细过程见下:

可以注意到,在一次迭代里,模型D的参数可以更新k次(但是作者考虑到成本问题,设k=1),而模型G的参数只更新一次。此外,模型D的训练是梯度上升法,模型G的训练是梯度下降法。作者还使用了momentum优化算法。
在模型G的训练早期,真实数据和假数据差别比较大,模型D可以轻易将其区分,即$\log (1-D(G(\mathbf z)))$总是接近于0,减缓了梯度学习的过程,所以在模型G的训练早期,其目标函数可以改为最大化$\log D(G(z))$,以获得更强有力的梯度,从而加快学习。
4.Theoretical Results
先定义一些符号,$\mathbf z$为噪声图像,$p_{\mathbf z}$为噪声图像的概率分布,即有$\mathbf z \sim p_{\mathbf z}$。得到的生成图像$G(\mathbf z)$服从概率分布$p_g$。真实的样本图像服从概率分布$p_{data}$。
图像的概率分布可视为连续型概率分布。
4.1.Global Optimality of $p_g = p_{data}$
本部分旨在证明上述模型存在全局最优解:$p_g = p_{data}$。即生成的图像和真实图像无法被区分,二者有着一样的概率分布。
首先对于任何的模型G,我们先考虑只优化模型D。
【命题1(proposition 1)】给定G,最优的D为:
\[D^*_G(\mathbf x)=\frac{p_{data}(\mathbf x)}{p_{data}(\mathbf x) + p_g(\mathbf x)} \tag{2}\]【证明】模型D的训练准则为:给定模型G,最大化下式:
\[\begin{align} V(G,D) &= \int_{\mathbf x} p_{data} (\mathbf x) \log( D(\mathbf x)) dx + \int_{\mathbf z} p_{\mathbf z} (\mathbf z) \log (1-D(g(\mathbf z)))dz \\&= \int_{\mathbf x} p_{data}(\mathbf x) \log (D(\mathbf x))+p_g(\mathbf x) \log(1-D(\mathbf x))dx \tag{3} \end{align}\]式(3)的第二行其实就是对数似然估计。可理解为,对于任意样本$\mathbf x$,其来自真实样本分布的概率乘上被模型D正确识别的概率,再加上其来自生成样本分布的概率乘上被模型D正确识别的概率(即$(1-D(x))$为模型D将样本$\mathbf x$判定为生成数据的概率),而我们的目标就是最大化这个值。
计算$V(G,D)$对D的导数并使其等于0(注意是对D求导,不是对$\mathbf x$求导),便可得到式(2),即当$D=D^*_G$时,式(3)取到最大值。
式(2)代入式(3)可得:
\[\begin{align} C(G) &= \max \limits_{D} V(G,D) \\&= \mathbb{E}_{\mathbf x \sim p_{data}} [\log D^*_G(\mathbf x)] + \mathbb{E}_{\mathbf z \sim p_{\mathbf z}} [\log (1-D^*_G(G(\mathbf z)))] \\&= \mathbb{E}_{\mathbf x \sim p_{data}}[\log D^*_G(\mathbf x)] + \mathbb{E}_{\mathbf x \sim p_g} [ \log(1-D^*_G(\mathbf x))] \\&= \mathbb{E}_{\mathbf x \sim p_{data}} \left[ \log \frac{p_{data}(\mathbf x)}{p_{data}(\mathbf x)+p_g (\mathbf x)} \right] + \mathbb{E}_{\mathbf x \sim p_g} \left[ \log \frac{p_g(\mathbf x)}{p_{data}(\mathbf x)+p_g(\mathbf x)} \right] \end{align}\tag{4}\]在代入最优的模型D后,我们接下来就该找到一个G来最小化$C(G)$了。
【定理1(Theorem 1)】当且仅当$p_g=p_{data}$时,$C(G)$取到全局最小值,为$-\log 4$。
【证明】假设存在某一模型G,使得$p_g = p_{data}$,此时有$D^*_G(\mathbf x)=\frac{1}{2}$。代入式(4),便可得到$C(G)=\log \frac{1}{2}+\log \frac{1}{2}=-\log 4$:
\[\mathbb{E}_{\mathbf x \sim p_{data}} [-\log 2]+\mathbb{E}_{\mathbf x \sim p_g} [-\log 2]=-\log 4\]如果定理1成立的话,那么$-\log 4$应该就是$C(G)$的最小值了。但如果是对于任意的一个模型G,式(4)也可写为:
\[C(G)=\int_{\mathbf x} p_{data} (\mathbf x) \log (\frac{p_{data}(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)})+p_G(\mathbf x)\log (\frac{p_G(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)}) dx \tag{4.1}\]将式(4.1)变换为:
\[C(G)=\int_{\mathbf x}(\log 2-\log2)p_{data}(\mathbf x)+p_{data} (\mathbf x) \log (\frac{p_{data}(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)})+(\log 2-\log 2)p_G(\mathbf x)+p_G(\mathbf x)\log (\frac{p_G(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)}) dx \tag{4.2}\]式(4.2)化简合并后得:
\[C(G)=-\log 2\int_{\mathbf x} p_G(\mathbf x)+p_{data}(\mathbf x)dx+\int_{\mathbf x} p_{data}(\mathbf x) (\log 2+ \log (\frac{p_{data}(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)}))+p_G(\mathbf x)(\log 2+\log(\frac{p_G(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)}))dx \tag{4.3}\]接下来我们来逐个化简式(4.3)中的每一项。
因为概率密度的定义,$p_G$和$p_{data}$在它们积分域上的积分等于1,即:
\[-\log 2\int_{\mathbf x} p_G(\mathbf x)+p_{data}(\mathbf x)dx=-\log 2(1+1)=-2\log 2=-\log 4 \tag{4.4}\]此外,根据对数的定义,我们有:
\[\log 2+\log(\frac{p_{data}(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)})=\log(2 \frac{p_{data}(\mathbf x)}{p_G(\mathbf x)+p_{data}(\mathbf x)})=\log(\frac{p_{data}(\mathbf x)}{(p_G(\mathbf x)+p_{data}(\mathbf x))/2}) \tag{4.5}\]把式(4.4)和式(4.5)代入式(4.3)可得:
\[C(G)=-\log 4+\int_{\mathbf x}p_{data}(\mathbf x) \log(\frac{p_{data}(\mathbf x)}{(p_G(\mathbf x)+p_{data}(\mathbf x))/2}) dx + \int_{\mathbf x}p_G(\mathbf x) \log(\frac{p_G(\mathbf x)}{(p_G(\mathbf x)+p_{data}(\mathbf x))/2}) dx \tag{4.6}\]代入KL散度(详见本文第9部分),式(4.6)可变为:
\[C(G) = -\log(4) + KL(p_{data} \parallel \frac{p_{data}+p_g}{2}) + KL(p_g \parallel \frac{p_{data}+p_g}{2})\tag{5}\]因为KL散度是非负的,所以得出结论$C(G)$最小是$-\log (4)$。那我们现在的证明就只差一个$p_g=p_{data}$时,$C(G)$才能取得最小值。
将式(5)改写为JS散度(详见本文第10部分):
\[C(G) = -\log(4)+2\cdot JSD(p_{data} \parallel p_g) \tag{6}\]根据JS散度的性质,当$p_{g}=p_{data}$时,$JSD(p_{data} \parallel p_g)$取到最小值,为0。此时,$C(G)$也取到最小值,为$-\log (4)$。
至此,定理1得证。
4.2.Convergence of Algorithm 1
本小节主要证明了该算法是可以收敛至$p_{g}=p_{data}$的。证明部分不再详述。
5.Experiments
我们训练对抗网络(包含G和D)使用了多个数据集:MNIST、TFD(the Toronto Face Database)、CIFAR-10。生成网络(即G)使用了ReLU和sigmoid激活函数,而识别网络(即D)使用的激活函数为maxout(见本文第8部分)。在训练识别网络时使用了dropout。虽然我们的理论框架允许在生成网络的中间层也使用dropout或添加其他噪声,但是我们并没有这样做,我们只是将噪声作为生成网络的输入。
经过训练后的模型G生成的图像见Fig2:

在Fig2中,每个block的前五列为模型G生成的图像,第六列为和第五列最为相似的训练数据。可以看出,生成的图像并不是训练数据的copy。Fig2(a)来自MNIST数据集,Fig2(b)来自TFD数据集,Fig2(c)和Fig2(d)来自CIFAR-10数据集。
6.Advantages and disadvantages
GAN的一个缺点就是在训练过程中,模型D和模型G的更新要很好的同步。首先,模型D如果训练的过好(相比于同期的模型G来说),那么会导致训练模型G时梯度消失,模型G的loss降不下去。而如果模型D训练的过差(相比于同期的模型G来说),又会导致模型G的梯度不准。所以模型D必须得训练的不好不坏才行(即和同期的模型G很好的同步)。此外,模型G也不应该被训练的过好(相比于同期的模型D),这会使得模型G生成图像趋向于和训练数据一模一样,就像直接copy训练数据一样,这显然也不是我们希望的(我们希望的是生成图像和$p_{data}$的分布一样,其具有一定的自创性,并不是完全的一样)。这也是GAN训练难问题的原因所在。
GAN的优点是不再需要马尔科夫链和近似推理。
7.Conclusions and future work
作者在本部分提出了对GAN可进行的一些简单的扩展,本博客不再详述。
8.maxout激活函数
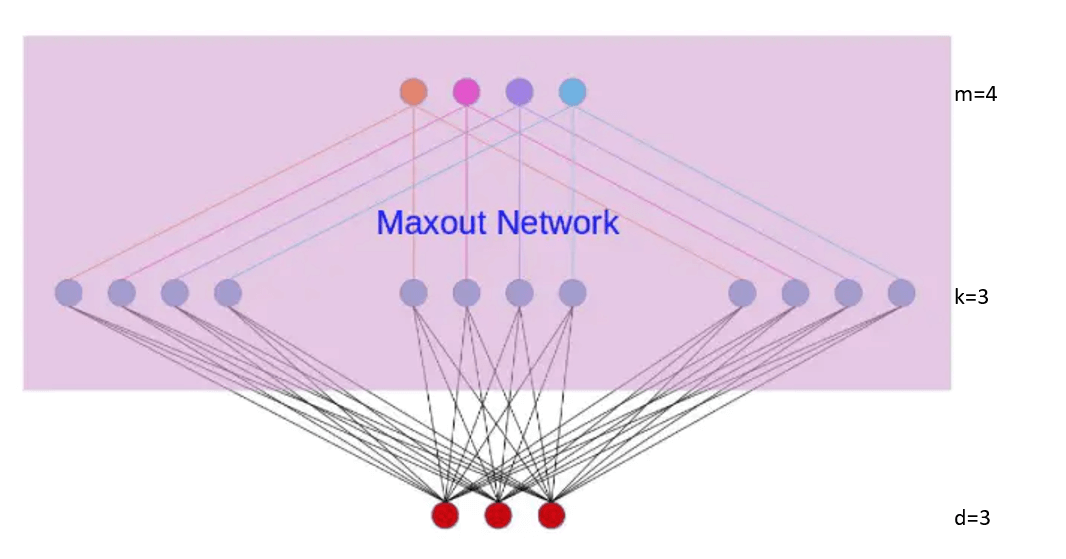
maxout network可以看做是在两个相邻隐藏层之间又加入了一个激活函数层。隐藏层节点的输出表达式为:
\[h_i(x)=\max \limits_{j \in [1,k]} \ z_{ij}\] \[where \ z_{ij}=x^TW_{...ij}+b_{ij}, \ and\ W\in \mathbb{R}^{d\times m \times k}\]W是三维的。d为上一层的神经元数目(本例中d=3);m为相邻的下一层的神经元数目(本例中m=4),k为激活函数层的节点数(本例中k=3)。maxout激活函数是非线性的。
9.KL散度
相对熵(relative entropy),又被称为Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是两个概率分布(probability distribution)间差异的非对称性度量。在信息理论中,相对熵等价于两个概率分布的信息熵(Shannon entropy)的差值。
相对熵是一些优化算法,例如最大期望算法(Expectation-Maximization algorithm,EM)的损失函数。此时参与计算的一个概率分布为真实分布,另一个为理论(拟合)分布,相对熵表示使用理论分布拟合真实分布时产生的信息损耗。
9.1.定义
设$P(x),Q(x)$是随机变量$X$上的两个概率分布,则在离散和连续随机变量的情形下,相对熵的定义分别为:
\[KL(P \parallel Q)=\sum P(x) \log \frac{P(x)}{Q(x)}\] \[KL(P \parallel Q)=\int P(x) \log \frac{P(x)}{Q(x)} dx\]公式的推导在此处不再赘述。
9.2.计算实例
假如一个字符发射器,随机发出0和1两种字符,真实发出概率分布为A,但实际不知道A的具体分布。通过观察,得到概率分布B与C,各个分布的具体情况如下:
\[A(0)=\frac{1}{2},A(1)=\frac{1}{2}\] \[B(0)=\frac{1}{4},B(1)=\frac{3}{4}\] \[C(0)=\frac{1}{8},C(1)=\frac{7}{8}\]可以计算出得到如下:
\[KL(A \parallel B)=\frac{1}{2} \log (\frac{1/2}{1/4}) + \frac{1}{2} \log (\frac{1/2}{3/4})=\frac{1}{2}\log (\frac{4}{3})\] \[KL(A \parallel C)=\frac{1}{2} \log (\frac{1/2}{1/8}) + \frac{1}{2} \log (\frac{1/2}{7/8})=\frac{1}{2}\log (\frac{16}{7})\]从分布上可以看出,实际上B要比C更接近实际分布(因为其与分布A的相对熵更小)。
9.3.性质
【非负性】相对熵恒为非负:$KL(P \parallel Q) \geqslant 0$,且在$P \equiv Q$时取0。
【不对称性】即$KL(P \parallel Q) \neq KL(Q \parallel P)$。在优化问题中,若P表示随机变量的真实分布,Q表示理论或拟合分布,则$KL(P \parallel Q)$被称为前向KL散度(forward KL divergence),$KL(Q \parallel P)$被称为后向KL散度(backward KL divergence)。
10.JS散度
JS散度(Jensen-Shannon)度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。一般地,JS散度是对称的(即$JS(P_1 \parallel P_2) = JS(P_2 \parallel P_1)$),其取值是0到1之间。定义如下:
\[JS(P_1 \parallel P_2) = \frac{1}{2} KL(P_1 \parallel \frac{P_1+P_2}{2} )+ \frac{1}{2}KL(P_2 \parallel \frac{P_1+P_2}{2})\]如果有$P_1 = P_2$,则此时$JS(P_1 \parallel P_2)=0$,即这两个概率分布完全一样。