本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.INTRODUCTION

边界追踪（border following）是二值图像处理的一个基本技术。本文提出了一种具有拓扑分析能力（topological analysis capability）的边界追踪算法。边界分为两种类型：外边界（the outer borders）和洞边界（the hole borders）。

2.BASIC CONCEPT AND NOTATIONS

本文只考虑二值图像。

图像最上、最下、最左、最右的四条边共同组成frame。像素值为0的点记为0-pixel，像素值为1的点记为1-pixel。为了不失一般性，我们假定构成frame的均为0-pixel。我们还假定在处理过程中，可以为像素点赋予任何整数值。像素点坐标用$(i,j)$表示。其中，i为行，j为列，i的排序从最上到最下，j的排序从最左到最右。点$(i,j)$处的像素值为$f_{i,j}$，所以一幅图像可以表示为像素点的集合：$F=\{ f_{i,j} \}$。

0-pixel连接而成的区域称为0-component，1-pixel连接而成的区域称为1-component。如果某一0-component包含frame，则我们称该0-component为背景（background），否则称该0-component为洞（hole）。

为了避免拓扑矛盾，如果1-pixel考虑4邻域，则0-pixel考虑8邻域；相反，如果1-pixel考虑8邻域，则0-pixel考虑4邻域。

【定义1（边界点）】：如果某一1-pixel的8邻域（或4邻域）内有一个为0-pixel，则称该1-pixel为边界点（border point），即0-component和1-component的边界点。

【定义2（相邻component的包围性）】：对于一幅二值图像的两个相邻component（two connected components）：$S_1$和$S_2$，如果$S_1$中任何一个像素点从任何一个方向（共考虑4个方向）到达frame的路径上都存在$S_2$的像素点，则称$S_2$包围了$S_1$。如果$S_2$包围了$S_1$，且$S_1$和$S_2$之间存在边界点（见定义1），则称$S_2$直接包围了$S_1$。

【定义3（外边界和洞边界）】：如果0-component直接包围1-component，则称二者之间的边界为外边界（outer border）；如果1-component直接包围了洞（即非背景的0-component），则称二者之间的边界为洞边界（hole border）。需要注意的是，不管是外边界还是洞边界，指的都是1-pixel（见定义1）。

以下属性适用于相邻的component和边界：

【性质1】对于任意的1-component，其外边界有且仅有一个；对于任意的洞，其洞边界有且仅有一个。

【定义4（父边界）】：外边界（假设0-component为$S_2$，其直接包围的1-component为$S_1$）的父边界定义如下：

如果$S_2$为一个洞，则外边界的父边界定义为$S_2$的洞边界。
如果$S_2$是背景，则外边界的父边界定义为frame。

假设有洞$S_3$和1-component $S_4$，且$S_4$直接包围$S_3$，此时形成的洞边界的父边界定义为$S_4$和直接包围$S_4$的0-component之间的外边界。

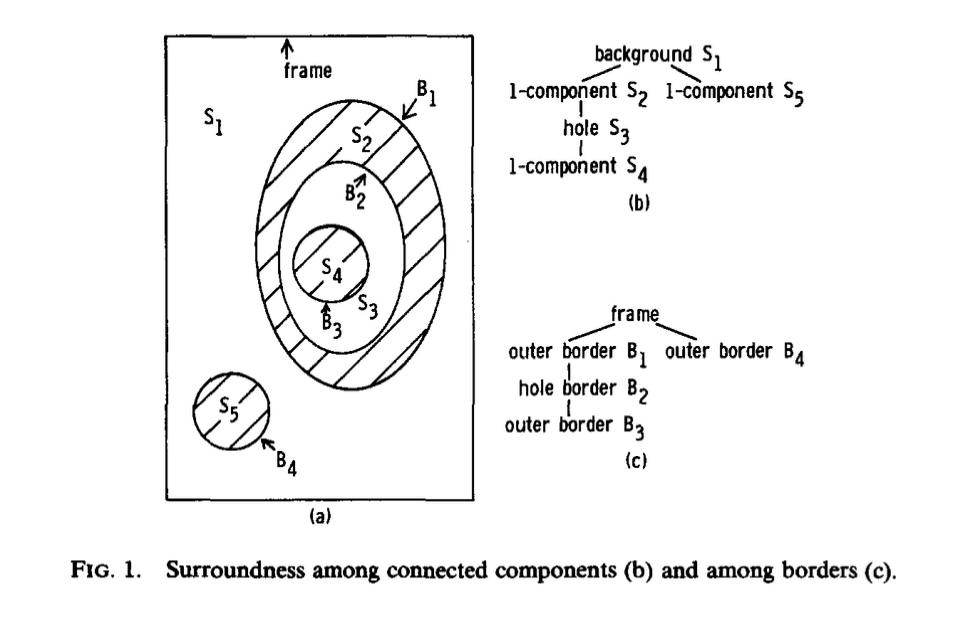
【定义5（边界的包围性）】：如果存在一系列边界$B_0,B_1,…,B_n$，对于任意k（$1\leqslant k \leqslant n$），都有$B_k$是$B_{k-1}$的父边界，则称边界$B_n$包围了边界$B_0$。

以上定义的图示举例：

3.THE BORDER FOLLOWING ALGORITHM FOR TOPOLOGICAL ANALYSIS

首先，我们给出了该算法的非正式解释。

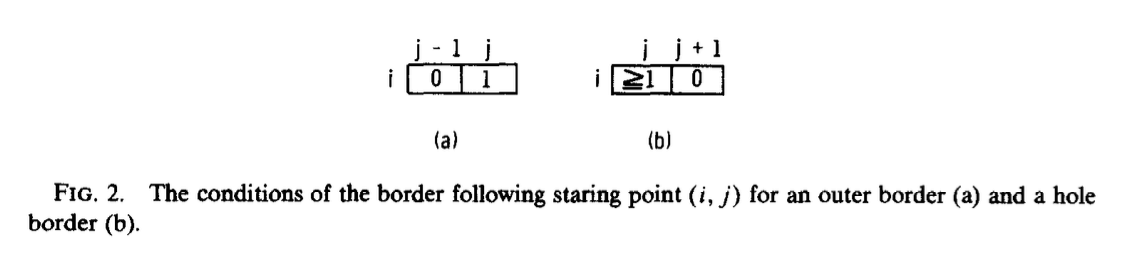
【算法1】对给定的二值图像进行光栅扫描（raster scan），寻找外边界或洞边界的起始点。外边界的起始点定义见Fig2(a)，洞边界的起始点定义见Fig2(b)。如果某一像素点$(i,j)$即满足外边界起始点又满足洞边界起始点，则将其视为外边界起始点。此外，为新找到的边界指定一个唯一可识别的编号，称之为边界的序号，并用NBD表示。

光栅扫描：是指从左往右，由上往下，先扫描完一行，再移至下一行起始位置继续扫描。

NBD：the sequential number of the current border。

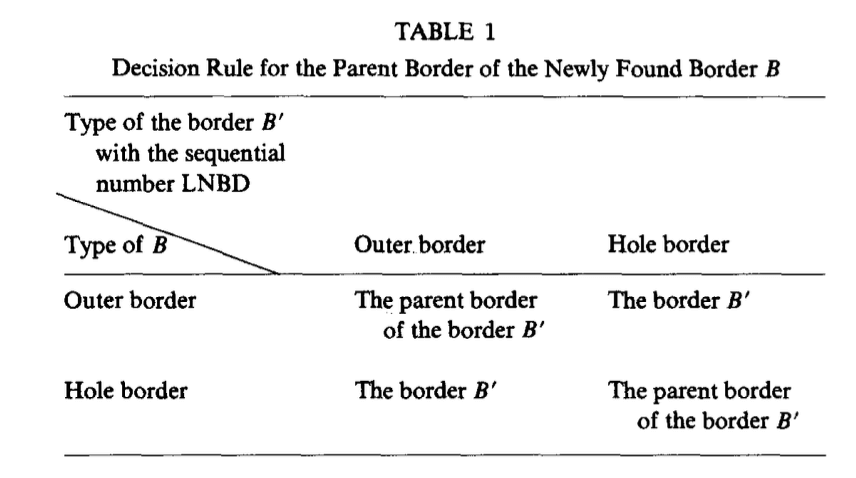
接下来确定新找到的边界的父边界。假设LNBD为找到该新边界之前上一个找到的边界的序号。序号为LNBD的边界要么是当前边界的父边界，要么和当前边界有着同一父边界：

一些标记的规则：

（a）如果当前边界位于0-component（包含像素点$(p,q+1)$）和1-component（包含像素点$(p,q)$）之间，则将像素点$(p,q)$的序号取负数，即为-NBD（即一个外边界最右边的像素点被标记成-NBD）。

（b）否则，像素点$(p,q)$的序号依然为NBD，除非像素点在一个已经跟踪过的边界上。

规则(a)和规则(b)确保了像素点$(p,q)$不会再次成为另一个洞边界或外边界的起始点。

当找到并标记完一个边界后，从头开始光栅扫描，直到光栅扫描可以走到最后（即图片的右下角）时，算法结束。

算法的详细说明见APPENDIX I。

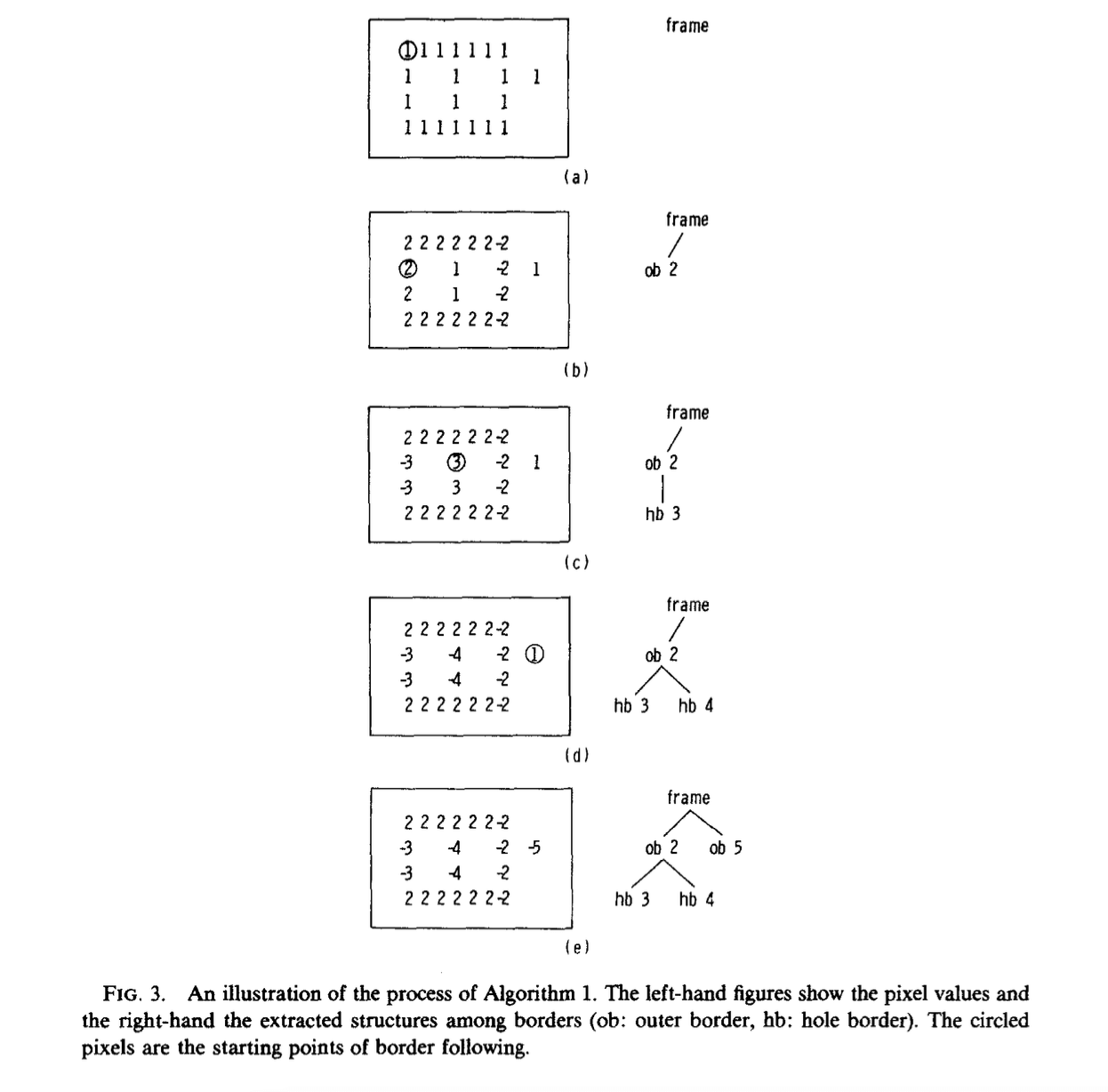
接下来尝试推导一下Fig3所示的流程。假设有二值图像：

\[\begin{bmatrix} 0 & 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0& 0& 1& 0& 0& 1& 0& 0& 1& 0& 1& 0 \\ 0& 0& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \end{bmatrix}\]

最外围一圈为frame，NBD=1。从(0,0)开始光栅扫描。

$(i,j) \leftarrow (1,2)$为外边界起始点。NBD=2。$(i_2,j_2) \leftarrow (1,1)$。
以(1,2)为中心，从(1,1)开始顺时针寻找（假设1-pixel考虑8邻域，0-pixel考虑4邻域）非0像素点，找到(1,3)。$(i_1,j_1) \leftarrow (1,3)$。
$(i_2,j_2) \leftarrow (i_1,j_1)$，即(1,3)。$(i_3,j_3) \leftarrow (i,j)$，即(1,2)。
以(1,2)为中心，从(0,3)（即(1,3)的下一个像素点开始）开始逆时针寻找非0的像素点，找到(2,2)。$(i_4,j_4) \leftarrow (2,2)$。
进入第4.2步，$f_{1,2}=2$。
\[\begin{bmatrix} 0 & 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 & 0 & 2 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0& 0& 1& 0& 0& 1& 0& 0& 1& 0& 1& 0 \\ 0& 0& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \end{bmatrix}\]
$(i_2,j_2) \leftarrow (i_3,j_3)$，即(1,2)。$(i_3,j_3) \leftarrow (i_4,j_4)$，即(2,2)。回到第3.3步。
以(2,2)为中心，从(1,2)的下一个像素(1,1)开始逆时针寻找第一个非0像素点，找到(3,2)。$(i_4,j_4) \leftarrow (3,2)$。
进入第4.2步，修改$f_{2,2}=2$。
\[\begin{bmatrix} 0 & 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 & 0 & 2 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0& 0& 2& 0& 0& 1& 0& 0& 1& 0& 1& 0 \\ 0& 0& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \end{bmatrix}\]
$(i_2,j_2) \leftarrow (i_3,j_3)$，即(2,2)。$(i_3,j_3) \leftarrow (i_4,j_4)$，即(3,2)。回到第3.3步。

后续的步骤与上述类似，不再赘述。以下属性显示了算法1的有效性。

【性质3】对于任意1-component $S_1$，其最上面一行最左侧的像素点$(i,j)$一定符合Fig2(a)。从$(i,j)$开始找到的边界为外边界，且仅会被找到一次（不会被重复找到）。

证明见原文Appendix II，本博客不再详述。

【性质4】洞$S_1$最上面一行最左侧的像素点$(i,j+1)$（和像素点$(i,j)$）一定符合Fig2(b)。根据Fig2(b)找到的一定是洞边界，且每个洞边界也只会被找到一次。

证明类似于性质3的证明，不再赘述。

【性质5】算法1的边界起始点和1-components或者洞一一对应。

此性质可由性质3和性质4直接推导出。

【性质6】即Table1。

证明见原文Appendix III，本博客不再详述。

本算法的优势：

我们不但能找到1-components和holes，我们还能统计出其各自的数量。
我们可以将1-components或holes视为单独的一个像素点。
此外我们还可以对边界的特征进行一些限制。例如，限制1-components所在矩形框的面积必须大于某一特定的阈值。
该算法所得到的相邻component的包围性可用于图像搜索或图像特征提取。
由算法1得到的边界可以是一种有效的图像存储方法。因为其可以在不恢复原始图像的情况下执行一些简单的图像处理。例如，获取边界的特征（比如components的周长和面积）和分析拓扑结构（比如components的相邻关系）等。

由算法1得到的边界间的拓扑结构表示见Fig4：

4.THE BORDER FOLLOWING ALGORITHM FOR EXTRACTING ONLY THE OUTERMOST BORDERS

我们可以对算法1进行修改，使其只提取二值图像的最外层边界（the outermost borders）。最外层边界指的是背景和1-component之间的外边界。

【算法2】这里我们只列出与算法1不同的地方。（1）我们只从外边界的起始点（即Fig2(a)）开始边界追踪，并且有$LNBD \leqslant 0$。（2）标记策略和算法1基本相同，唯一的不同是数值”2”和”-2”分别用”NBD”和”-NBD”代替。（个人理解：每次更新NBD时，都会同步替换之前值为2或-2的点）（3）在光栅扫描过程中，我们会保存最新遇到的非0像素点的LNBD的值。每当我们开始新的一行的扫描时，重置LNBD为0。

算法2的原理解释如下。最外层边界的父边界为frame。当边界点$(i,j)$满足以下两种情况中的一个时，其为最外层边界：

$(i,1),(i,2),…,(i,j-1)$均为0-pixel。
$(i,h)$为光栅扫描最新遇到的外边界点，且$(i,h+1)$属于背景。

情况1和情况2可分别通过LNBD=0和LNBD=-2来检查。

【性质7】针对二值图像，算法2仅追踪最外层边界（可能不止一个，但是每个只追踪一次）。

5.CONCLUSION

对全文的总结，不再详述。

6.APPENDIX I: THE FORMAL DESCRIPTION OF ALGORITHM 1

假设输入图像为$F=\{ f_{ij} \}$，设置初始NBD=1，并将其作为frame的序号（即frame的NBD为1）。然后对图像进行光栅扫描，对于$f_{ij}\neq 0$的像素点执行以下步骤。每次开始扫描新的一行时，重置LNBD为1。

选择以下某一项继续：
1. 如果$f_{ij}=1$且$f_{i,j-1}=0$，则像素点$(i,j)$为外边界的起始点（如Fig2(a)）所示。NBD+=1。$(i_2,j_2) \leftarrow (i,j-1)$（可理解为将$(i,j-1)$赋给$(i_2,j_2)$）。
2. 如果$f_{ij} \geqslant 1$且$f_{i,j+1}=0$，则像素点$(i,j)$为洞边界的起始点（如Fig2(b)）所示。NBD+=1。$(i_2,j_2)\leftarrow (i,j+1)$。如果有$f_{ij}>1$，则$LNBD \leftarrow f_{ij}$。
3. 其他情况，跳转至第4步。
根据Table1，确定第1步中新找到的边界的父边界。
从第1步中找到的边界起始点$(i,j)$开始，按照3.1-3.5进行边界追踪。
1. 从$(i_2,j_2)$开始，以$(i,j)$为中心（4邻域或8邻域），顺时针寻找第一个不为0的像素点$(i_1,j_1)$。如果转一圈仍没有找到不为0的像素点，则$f_{ij} \leftarrow -NBD$，并且跳转到第4步。
2. $(i_2,j_2) \leftarrow (i_1,j_1)$，$(i_3,j_3) \leftarrow (i,j)$。
3. 以$(i_3,j_3)$为中心，按照逆时针方向，从$(i_2,j_2)$的下一个像素点开始，寻找第一个不为0的像素点$(i_4,j_4)$。
4. 按照以下步骤修改像素点$(i_3,j_3)$的像素值$f_{i_3,j_3}$：
  1. 如果在第3.3步中，在逆时针转圈的过程中，已经检查过像素点$(i_3,j_3+1)$，且其像素值为0，则$f_{i_3,j_3} \leftarrow -NBD$。
  2. 如果像素点$(i_3,j_3+1)$没有在第3.3步中检查过或在第3.3步检查过但其像素值不是0（即不是第3.3步中检查过的0像素点），并且有$f_{i_3,j_3}=1$，则$f_{i_3,j_3} \leftarrow NBD$。
  3. 其他情况不修改$f_{i_3,j_3}$的值。
5. 如果有$(i_4,j_4)=(i,j)$且$(i_3,j_3)=(i_1,j_1)$，则跳转到第4步。否则，$(i_2,j_2) \leftarrow (i_3,j_3),(i_3,j_3) \leftarrow (i_4,j_4)$，并回到第3.3步。
如果$f_{ij} \neq 1$，则执行$LNBD \leftarrow \lvert f_{ij} \rvert$，然后从$(i,j+1)$继续光栅扫描。当光栅扫描达到右下角时停止算法。

NBD并不是每次都赋给$f_{ij}$，参照算法流程，只有执行$f_{ij} \leftarrow NBD$时才把NBD赋值给$f_{ij}$。

7.原文链接

👽Topological Structural Analysis of Digitized Binary Images by Border Following

【论文阅读】Topological Structural Analysis of Digitized Binary Images by Border Following

Border Following，cv::findContours原理