【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.误差-分歧分解
在【机器学习基础】第二十七课:集成学习之个体与集成一文中,欲构建泛化能力强的集成,个体学习器应“好而不同”。现在我们来做一个简单的理论分析。
假定我们用个体学习器$h_1,h_2,…,h_T$通过加权平均法结合产生的集成来完成回归学习任务$f:\mathbb{R}^d \mapsto \mathbb{R}$。对示例$\mathbf{x}$,定义学习器$h_i$的“分歧”(ambiguity)为:
\[A(h_i \mid \mathbf{x})= (h_i(\mathbf{x})-H(\mathbf{x}))^2 \tag{1}\]其中,$H(\mathbf{x})$为集成得到的模型:
\[H(\mathbf{x})=\sum^T_{i=1} w_i h_i (\mathbf{x}) \tag{2}\]则集成的“分歧”是:
\[\begin{align} \bar{A}(h\mid \mathbf{x}) &= \sum^T_{i=1} w_i A(h_i \mid \mathbf{x}) \\&= \sum^T_{i=1} w_i (h_i(\mathbf{x})-H(\mathbf{x}))^2 \end{align} \tag{3}\]显然,这里的“分歧”项表征了个体学习器在样本$\mathbf{x}$上的不一致性,即在一定程度上反映了个体学习器的多样性。个体学习器$h_i$和集成$H$的平方误差分别为:
\[E(h_i \mid \mathbf{x})=(f(\mathbf{x})-h_i(\mathbf{x}))^2 \tag{4}\] \[E(H \mid \mathbf{x})=(f(\mathbf{x})-H(\mathbf{x}))^2 \tag{5}\]令$\bar{E} (h\mid \mathbf{x})=\sum^T_{i=1} w_i \cdot E(h_i \mid \mathbf{x})$表示个体学习器误差的加权均值,有:
\[\begin{align} \bar{A}(h\mid \mathbf{x}) &= \sum^T_{i=1} w_i (h_i(\mathbf{x})-H(\mathbf{x}))^2 \\&= \sum^T_{i=1} w_i (h_i(\mathbf{x})^2 -2h_i(\mathbf{x})H(\mathbf{x}) + H(\mathbf{x})^2) \\&= \sum^T_{i=1} w_i h_i(\mathbf{x})^2 -2\sum^T_{i=1} w_i h_i(\mathbf{x})H(\mathbf{x}) + \sum^T_{i=1} w_i H(\mathbf{x})^2 \\&= \sum^T_{i=1} w_i h_i(\mathbf{x})^2 -2 H(\mathbf{x}) \sum^T_{i=1} w_i h_i(\mathbf{x}) + H(\mathbf{x})^2 \sum^T_{i=1} w_i \\&= \sum^T_{i=1} w_i h_i(\mathbf{x})^2 -2 H(\mathbf{x}) \cdot H(\mathbf{x}) + H(\mathbf{x})^2 \\&= \sum^T_{i=1} w_i h_i(\mathbf{x})^2 -H(\mathbf{x})^2 \end{align} \tag{6}\]$\sum^T_{i=1} w_i =1$。
又:
\[\begin{align} \sum^T_{i=1} w_i E(h_i \mid \mathbf{x})-E(H\mid \mathbf{x}) &= \sum^T_{i=1} w_i (f(\mathbf{x})-h_i(\mathbf{x}))^2 - (f(\mathbf{x})-H(\mathbf{x}))^2 \\&= \sum^T_{i=1} w_i (f(\mathbf{x})^2 -2f(\mathbf{x})h_i(\mathbf{x}) + h_i(\mathbf{x})^2) - (f(\mathbf{x})^2 -2f(\mathbf{x})H(\mathbf{x}) + H(\mathbf{x})^2) \\&= f(\mathbf{x})^2 -2f(\mathbf{x}) \sum^T_{i=1} w_i h_i(\mathbf{x}) + \sum^T_{i=1} w_i h_i(\mathbf{x})^2 - f(\mathbf{x})^2 +2f(\mathbf{x})H(\mathbf{x}) - H(\mathbf{x})^2 \\&= f(\mathbf{x})^2 -2f(\mathbf{x})H(\mathbf{x}) + \sum^T_{i=1} w_i h_i(\mathbf{x})^2 - f(\mathbf{x})^2 +2f(\mathbf{x})H(\mathbf{x}) - H(\mathbf{x})^2 \\&= \sum^T_{i=1} w_i h_i(\mathbf{x})^2 - H(\mathbf{x})^2 \end{align} \tag{7}\]结合式(6)和式(7)可得:
\[\begin{align} \bar{A}(h\mid \mathbf{x}) &= \sum^T_{i=1} w_i E(h_i \mid \mathbf{x})-E(H\mid \mathbf{x}) \\&= \bar{E} (h\mid \mathbf{x})- E(H\mid \mathbf{x}) \end{align} \tag{8}\]式(8)对所有样本$\mathbf{x}$均成立,令$p(\mathbf{x})$表示样本的概率密度,则在全样本上有(结合式(3)):
\[\sum^T_{i=1} w_i \int A(h_i \mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x}=\sum^T_{i=1} w_i \int E(h_i \mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x} - \int E(H\mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x} \tag{9}\]类似的,个体学习器$h_i$在全样本上的泛化误差和分歧项分别为:
\[E_i = \int E(h_i \mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x} \tag{10}\] \[A_i = \int A(h_i \mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x} \tag{11}\]集成的泛化误差为:
\[E=\int E(H\mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x} \tag{12}\]将式(10)-式(12)代入式(9),再令$\bar{E}=\sum^T_{i=1} w_i E_i$表示个体学习器泛化误差的加权均值,$\bar{A}=\sum^T_{i=1}w_i A_i$表示个体学习器的加权分歧值,有:
\[E=\bar{E}-\bar{A} \tag{13}\]式(13)明确提示出:个体学习器准确率越高、多样性越大,则集成越好。并将其称为“误差-分歧分解”(error-ambiguity decomposition)。
要想使泛化误差$E$越小,则可使$\bar{E}$越小,即个体学习器准确率越高;使$\bar{A}$越大,即多样性越大。
但是上述的推导过程只适用于回归学习,难以直接推广到分类学习任务上去。
2.多样性度量
顾名思义,多样性度量(diversity measure)是用于度量集成中个体分类器的多样性,即估算个体学习器的多样化程度。典型做法是考虑个体分类器的两两相似/不相似性。
亦称“差异性度量”。
给定数据集$D=\{ (\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_m,y_m) \}$,对二分类任务,$y_i \in \{-1,+1 \}$,分类器$h_i$与$h_j$的预测结果列联表(contingency table)为:
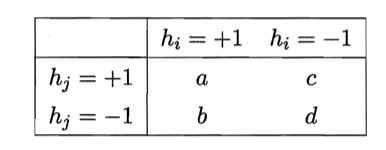
其中,a表示$h_i$与$h_j$均预测为正类的样本数目;b、c、d含义由此类推;$a+b+c+d=m$。基于这个列联表,下面给出一些常见的多样性度量。
👉不合度量(disagreement measure):
\[dis_{ij} = \frac{b+c}{m} \tag{14}\]$dis_{ij}$的值域为$[0,1]$。值越大则多样性越大。
👉相关系数(correlation coefficient):
\[\rho_{ij} = \frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}} \tag{15}\]$\rho_{ij}$的值域为$[-1,1]$。若$h_i$与$h_j$无关,则值为0;若$h_i$与$h_j$正相关则值为正,否则为负。
👉Q-统计量(Q-statistic):
\[Q_{ij}=\frac{ad-bc}{ad+bc} \tag{16}\]$Q_{ij}$与相关系数$\rho_{ij}$的符号相同,且$\lvert Q_{ij} \rvert \leqslant \lvert \rho_{ij} \rvert$。
👉$\kappa$-统计量($\kappa$-statistic):
\[\kappa = \frac{p_1-p_2}{1-p_2} \tag{17}\]其中,$p_1$是两个分类器取得一致的概率;$p_2$是两个分类器偶然达成一致的概率,它们可由数据集$D$估算:
\[p_1 = \frac{a+d}{m} \tag{18}\] \[p_2 = \frac{(a+b)(a+c)+(c+d)(b+d)}{m^2} \tag{19}\]若分类器$h_i$与$h_j$在$D$上完全一致,则$\kappa=1$;若它们仅是偶然达成一致,则$\kappa=0$。$\kappa$通常为非负值,仅在$h_i$与$h_j$达成一致的概率甚至低于偶然性的情况下取负值。
以上介绍的都是“成对型”(pairwise)多样性度量,它们可以容易地通过2维图绘制出来。例如著名的“$\kappa$-误差图”,就是将每一对分类器作为图上的一个点,横坐标是这对分类器的$\kappa$值,纵坐标是它们的平均误差,下图给出了一个例子。显然,数据点云的位置越高,则个体分类器准确性越低;点云的位置越靠右,则个体学习器的多样性越小。
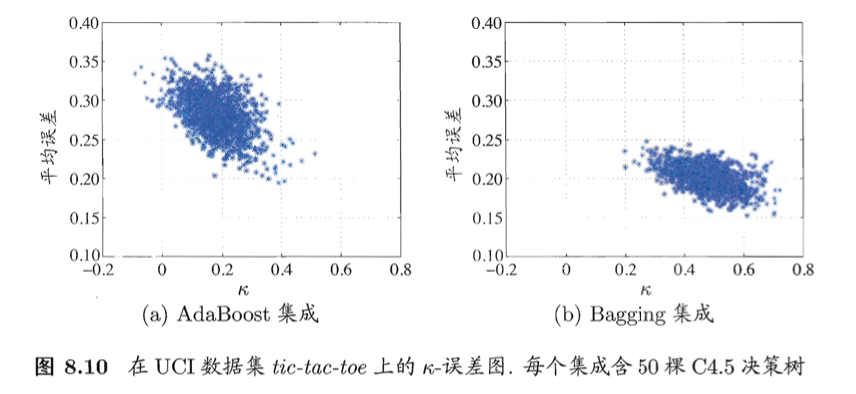
3.多样性增强
在集成学习中需有效地生成多样性大的个体学习器。与简单地直接用初始数据训练出个体学习器相比,如何增强多样性呢?一般思路是在学习过程中引入随机性,常见做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。不同的多样性增强机制可同时使用。有些方法甚至同时使用了更多机制。
3.1.数据样本扰动
给定初始数据集,可从中产生出不同的数据子集,再利用不同的数据子集训练出不同的个体学习器。
数据样本扰动法对“不稳定基学习器”很有效,例如决策树、神经网络等,训练样本稍加变化就会导致学习器有显著变动。
然而,有一些基学习器对数据样本的扰动不敏感,例如线性学习器、支持向量机、朴素贝叶斯、k近邻学习器等,这样的基学习器称为稳定基学习器,对此类基学习器进行集成往往需使用输入属性扰动等其他机制。
3.2.输入属性扰动
著名的随机子空间(random subspace)算法就依赖于输入属性扰动,该算法从初始属性集中抽取出若干个属性子集,再基于每个属性子集训练一个基学习器。对包含大量冗余属性的数据,在子空间中训练个体学习器不仅能产生多样性大的个体,还会因属性数的减少而大幅节省时间开销。同时,由于冗余属性多,减少一些属性后训练出的个体学习器也不至于太差。若数据只包含少量属性,或者冗余属性很少,则不宜使用输入属性扰动法。
3.3.输出表示扰动
此类做法的基本思路是对输出表示进行操纵以增强多样性。可对训练样本的类标记稍作变动,如“翻转法”(Flipping Output)随机改变一些训练样本的标记;也可对输出表示进行转化,如“输出调制法”(Output Smearing)将分类输出转化为回归输出后构建个体学习器;还可将原任务拆解为多个可同时求解的子任务,如ECOC法利用纠错输出码将多分类任务拆解为一系列二分类任务来训练基学习器。
3.4.算法参数扰动
基学习算法一般都有参数需进行设置,例如神经网络的隐层神经元数、初始连接权值等,通过随机设置不同的参数,往往可产生差别较大的个体学习器。对参数较少的算法,可通过将其学习过程中某些环节用其他类似方式代替,从而达到扰动的目的,例如可将决策树使用的属性选择机制替换成其他的属性选择机制。