本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.凸包
凸包相关内容请见:【数学基础】第十八课:凸优化基础。
2.Graham扫描算法
Graham’s scan是一种计算一组平面点凸包的算法,时间复杂度为$O(n\log n)$。
算法步骤与图解:
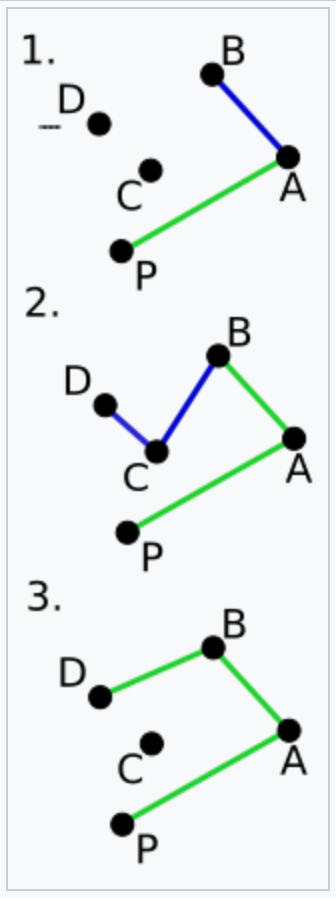
- 第一步:找到最下边的点,如果有多个点纵坐标都相同且都在最下方,则选取最左边的。在上图中这个点是P。这一步只需要扫描一遍所有的点即可,时间复杂度为$O(n)$。
- 第二步:将所有的点按照相对于第一步中得到的点P的极角大小进行排序。注意这一步并不需要真的通过计算反三角函数来获取与x轴夹角的大小。可以直接使用该点与P点连线的斜率,或者由P点到该点的向量与沿x轴单位向量的点积来减少计算量。可以使用诸如快速排序、堆排序之类的算法进行排序,时间复杂度为$O(n\log n)$。
- 维护一个栈(FILO),以保存当前的凸包。按第二步中排序得到的结果,依次将点加入到栈中,如果正在考虑的点与栈顶的两个点不是“向左转”的,就表明当前栈顶的点并不在凸包上,而我们需要将其弹出栈,重复这一个过程直到正在考虑的点与栈顶的两个点是“向左转”的。
- 刚开始的两个点P、A直接入栈。
- 在点B加入时,P->A->B就构成左转,因此直接加入点B即可。
- 接下来加入点C,A->B->C还是构成左转,因此直接加入点C。
- 继续加入点D时,B->C->D就变成右转了,此时可以观察到如果将BD连线,C将被包含在多边形的内部,因此点C出栈。注意需要继续检查A->B->D是左转还是右转,如果还是右转的话B点需要继续出栈,以此类推。这个例子比较简单,A->B->D已经是左转了,D点可以入栈。
- 最后回到P点,B->D->P是左转,算法完成,所求凸包为四边形PABD。
另外,如果发现三点共线的情况,算法可以考虑将其视为左转或者右转。这取决于究竟只是要求凸包的边界,还是要找到在凸包边界上所有的点。
3.相关API
1
2
3
4
5
6
void convexHull(
InputArray points,
OutputArray hull,
bool clockwise = false,
bool returnPoints = true
);
cv::convexHull基于2D点集寻找凸包,方法见本文第2部分。API参数解释:
InputArray points:输入的2D点集。OutputArray hull:输出检测到的凸包。如果为vector<int>,此时返回的是凸包上的点在输入2D点集中的索引;如果为vector<Point>,此时返回的就是凸包上的点的实际坐标。bool clockwise = false:表示参数2中的点是按顺时针方向还是逆时针方向。true为顺时针;false为逆时针。bool returnPoints = true:表示第2个参数的输出类型。如果为true,则参数2的类型为vector<Point>,否则为vector<int>。