本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
之前博客关于ResNet的简单介绍:【深度学习基础】第三十课:残差网络ResNets。
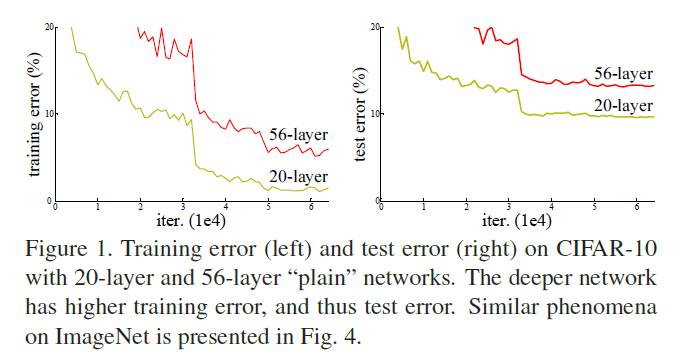
神经网络的深度对于网络的性能至关重要。那么一味的添加隐藏层就能获得更好的性能吗?回答这一问题的一大障碍就是梯度消失/爆炸。但是Batch Normalization在很大程度上解决了梯度消失/爆炸问题,因此我们可以继续这个问题,当网络深度一直增加时,模型准确率会上升至饱和,然后迅速下降(称该现象为“退化”(degradation)),并且这不是由过拟合造成的。Fig1给出了一个典型的例子:
在本文中,我们通过引入深度残差学习框架(a deep residual learning framework)来解决“退化”问题:
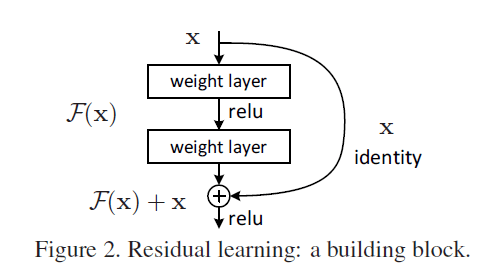
作者称这种跳跃性的连接(跨越一层或多层)为“shortcut connections”。
在ImageNet上实验发现:1)深度残差网络没有发生“退化”现象;2)相反,随着深度的增加,深度残差网络的准确率也会增加。此外,我们在CIFAR-10数据集上也成功训练了超过100层的网络模型,并尝试探索超过1000层的网络模型。
我们152层的残差网络效果比VGG好,并且复杂度还比VGG低。此外,ResNet还获得了以下比赛的第一名:
- ILSVRC2015 classification competition(top-5错误率为3.57%)
- ImageNet detection(ILSVRC2015)
- ImageNet localization(ILSVRC2015)
- COCO detection(COCO2015)
- COCO segmentation(COCO2015)
这说明我们所提出的残差网络不局限于某一特定数据集,其思想具有通用性。
2.Related Work
介绍他人的相关工作,本部分不再详述。
3.Deep Residual Learning
3.1.Residual Learning
本部分略,不再详述。
3.2.Identity Mapping by Shortcuts
如Fig2所示,将残差块定义为:
\[\mathbf{y}=\mathcal{F}(\mathbf{x},\{ W_i \})+\mathbf{x} \tag{1}\]其中,$\mathbf{x},\mathbf{y}$为残差块的输入和输出。$\mathcal{F}(\mathbf{x},\{ W_i \})$表示要学习的残差映射。例如在Fig2中,$\mathcal{F}=W_2 \sigma (W_1 \mathbf{x})$,$\sigma$表示ReLU激活函数(偏置项被省略)。$\mathcal{F}$和$\mathbf{x}$相加的方式为对应位置的元素相加(element-wise addition)。
式(1)既没有引入额外的参数,也没有增加计算复杂度。这使得我们可以在相同的参数量、网络深度、网络宽度以及计算成本下,公平的比较plain network和residual network。
在式(1)中,$x$和$\mathcal{F}$的维度必须一样。如果出现维度不一致的情况,则需要一个权重矩阵$W_s$使其保持一致:
\[\mathbf{y}=\mathcal{F} (\mathbf{x},\{ W_i \})+W_s \mathbf{x} \tag{2}\]注意$W_s$仅在维度匹配时使用。
$\mathcal{F}$的形式是灵活的,可跨越多层使用,本文使用的形式见Fig5(分别跨越两层和三层):
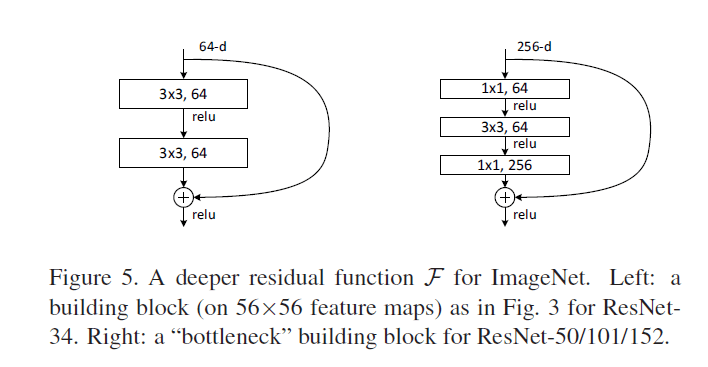
但是如果只跨越一层,这类似于线性层:$\mathbf{y} = W_1 x +x$,并没有显著的优势。
尽管上述是以FC层为例,但残差连接也同样适用于卷积层。
3.3.Network Architectures
我们测试了不同的plain/residual网络,并发现了一些一致的现象。为了后续的讨论,在这里列出在ImageNet上测试的两个模型。
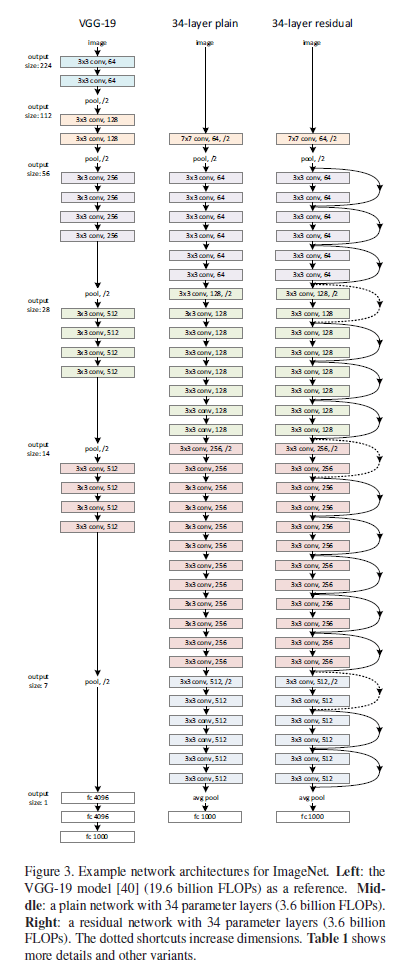
Fig3中,FLOPs全称为floating point operations,意为浮点运算数(即计算量,本文中计算量指的就是加法和乘法的次数,即multiply-adds)。FLOPs通常用于衡量模型或者算法的复杂度。
👉Plain Network
基于VGGNet(见Fig3左),我们创建了plain baseline(见Fig3中)。plain baseline大量使用了$3\times 3$的卷积核,并且plain baseline的构建有两个简单的原则:1)如果输出的feature map的size一样,则卷积核的数量也保持一样;2)如果输出的feature map的size减小一半,则卷积核的数量增加一倍。在plain baseline中,我们使用步长为2的卷积层进行下采样。plain baseline一共有34层。
此外,plain baseline比VGGNet(见Fig3左)使用了更少的卷积核,复杂度也更低。
👉Residual Network
基于plain baseline,我们添加了shortcut connections(见Fig3右),即将其转化成对应的残差网络。Fig3右中,实线shortcut connections表示输入和输出维度一致,虚线shortcut connections表示输入和输出维度不一致。对于维度不一致有两种解决办法:(A)不一致的部分用0补齐,这种方法的好处是不引入额外的参数;(B)采用式(2)的方法(可以通过$1\times 1$的卷积)。不管哪种方式,在本例中,当跨越的两层的feature map大小不一致时,都有步长为2。
3.4.Implementation
我们在ImageNet上的实现遵循了AlexNet和VGGNet中的一些操作。先将图像的短边随机resize到[256,480]的范围内(长边等比例缩放),然后从resize后的图像或resize后加了水平翻转的图像中随机裁剪出$224 \times 224$大小的图像,并将其中的每个像素都减去该坐标上所有像素值的平均。在每次卷积之后,激活函数之前,都应用了BN。按照论文“K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In ICCV, 2015.”初始化权重,plain和residual网络的训练都是train from scratch。使用MBGD,mini-batch size=256。初始学习率设为0.1,当loss不再明显下降时,将学习率除以10。模型共训练$60 \times 10^4$次迭代。weight decay设为0.0001,momentum参数设为0.9。我们没有使用dropout。
from scratch在英文中的意思就是“从零开始、从头开始、白手起家”,引申过来就是不使用预训练文件而直接进行训练。
测试阶段,对于比较研究,我们采用标准的10-crop作为测试。对于最优结果的获取,使用了和VGGNet一样的多尺度方法(图像的短边resize到{224,256,384,480,640})。
4.Experiments
4.1.ImageNet Classification
我们在ImageNet2012分类任务(1000个类别)上评估了我们的方法。训练集有128万张图像,验证集有5万张图像,测试集有10万张图像。我们在测试集上获得最终结果,使用top-1和top-5错误率。
👉Plain Networks
我们首先评估了18层和34层的plain网络。34层的plain网络见Fig3中间。18层的plain网络近似于34层plain网络的结构,详细结构请见表1:
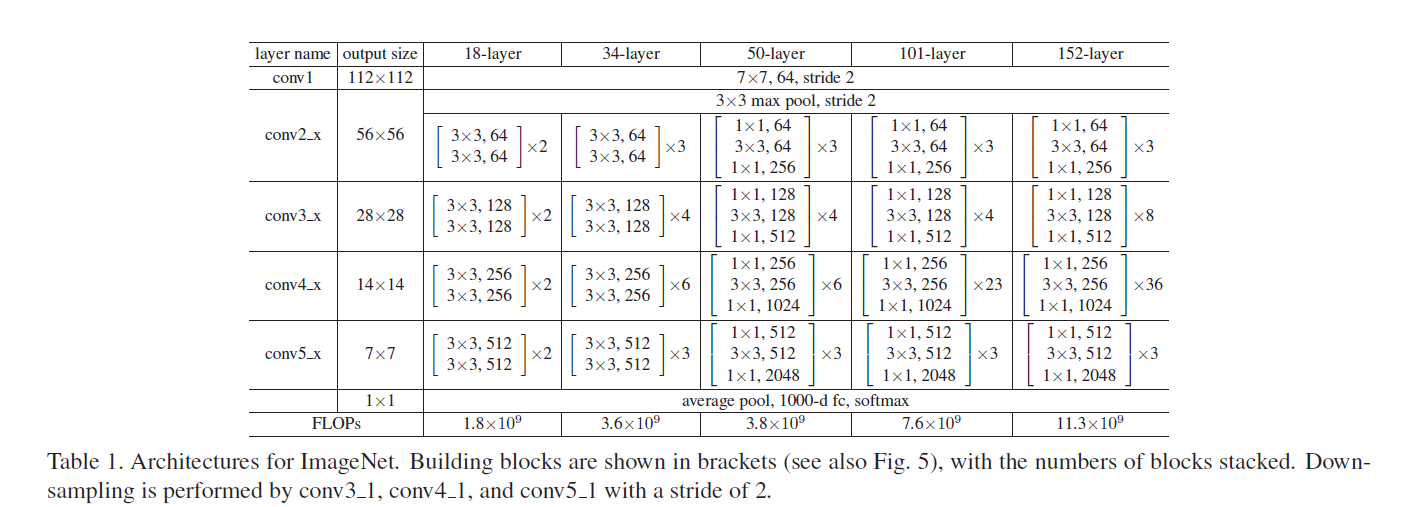
表1中,下采样发生在conv3_1,conv4_1,conv5_1(步长为2)。表1中每组括号都是一个残差块,其用到的残差连接见Fig5:

ResNet-34用的是跨越两层的连接,ResNet-50/101/152用的是跨越三层的连接。
结果见表2(top-1错误率,10-crop testing,ImageNet验证集):
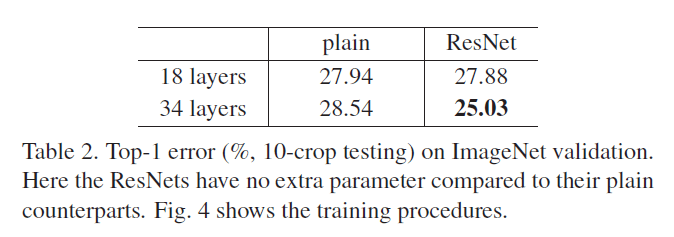
从表2可以看到,34层plain网络的错误率反倒比更浅的18层plain网络的错误率要高。为了揭示原因,我们比较了它俩在训练过程中,分别在训练集/验证集上的错误率(见Fig4左)。细的曲线为训练集错误率,粗的曲线为验证集错误率。我们发现了“退化”问题:在整个训练过程中,34层plain网络的训练集错误率一直高于18层plain网络的训练集错误率,尽管18层plain网络其实是34层plain网络的一个子集。
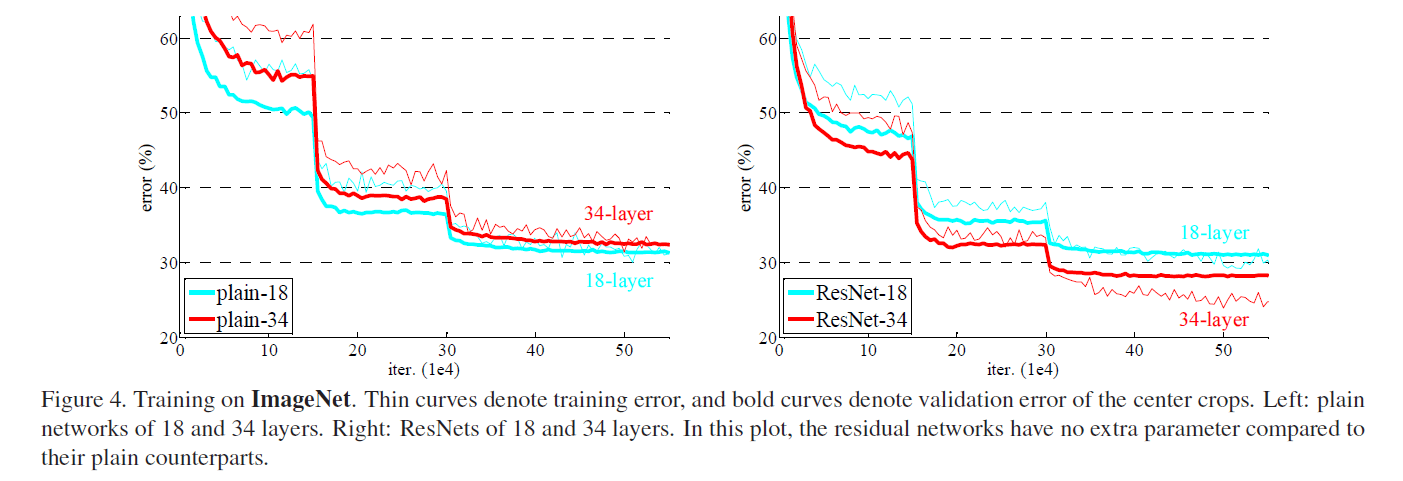
我们认为这种现象不太可能是由梯度消失引起的。这些网络在训练时都添加了BN,这确保了前向传播信号都有非0方差。并且我们也验证了反向传播的梯度确实也没有问题。因此无论是前向传播还是后向传播,信号都没有消失。事实上,34层plain网络也能取得不错的成绩(虽然没有18层plain网络好),见表3。我们猜测“退化”可能是因为深度plain网络收敛速度过慢,影响到了训练集错误率的下降。我们尝试了增加迭代次数(增加3倍),但依然观察到了“退化”现象,说明这个问题不能简单的只靠增加迭代次数来解决。这种优化困难的原因会在未来继续研究。
👉Residual Networks
接下来我们评估了18层residual网络和34层residual网络,即ResNet-18和ResNet-34。测试结果见表2和Fig4右,维度的不一致通过0 padding解决(option A),这样(相比对应的plain网络)就没有引入新的参数。
在表2和Fig4中,我们有3个主要的发现:
- 和plain网络的训练相反,ResNet-34的效果要比ResNet-18好(大约提升了2.8%)。更重要的是,ResNet-34得到了相当低的训练集错误率,并且这一现象可以推广到验证集。这表明残差连接可以很好的解决“退化”问题,这样我们就可以通过增加网络深度来提升准确率了。
- 相比34层plain网络,ResNet-34的top-1错误率下降了3.5%(见表2)。这验证了残差块在极深网络架构中的有效性。
- 最后,我们还注意到18层的plain网络和残差网络的准确率差不多(见表2),但是ResNet-18的收敛速度更快(见Fig4)。看来当网络不太深时,plain网络表现还可以。在这个案例中,残差块的主要优化贡献在于早期更快的收敛速度。
👉Identity vs. Projection Shortcuts
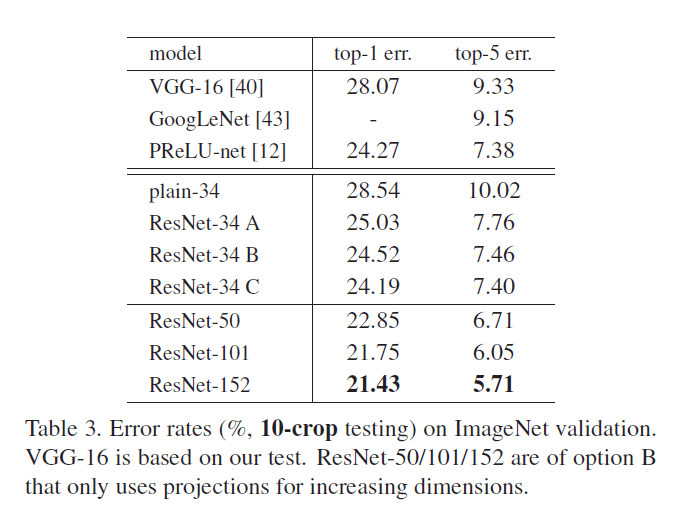
上面我们的讨论基于option A,结果显示还是有助于训练的。现在我们讨论下option B(即式(2))。在表3中,我们比较了三种option:(A)对于维度不一致的shortcut,使用0-padding(zero-padding shortcuts或identity shortcuts,即没有引进额外参数的shortcuts)使shortcut维度保持一致,所有的shortcut均没有引进额外的参数(表2和Fig4右用的都是这个option);(B)对于维度不一致的shortcut,引进额外的参数(即式(2),projection shortcuts,即引进了额外参数的shortcuts)使维度保持一致,剩余shortcut依旧不引进额外的参数;(C)所有的shortcut都使用式(2)引进额外的参数。
通过表3可以发现,所有的3种option效果都比plain网络好。option B略优于option A。我们认为这是因为option A使用0-padding,从而导致没有残差学习。option C略优于option B。我们认为这是因为引入了更多的额外参数。A/B/C之间微小的差异说明projection shortcuts(即引入额外参数的shortcuts)对于解决“退化”问题并不是必要的。因此,在本文的剩余部分中,我们不会使用option C,以降低内存/时间复杂度和模型大小。identity shortcuts不会增加瓶颈框架(the bottleneck architectures)的复杂度,这一性质尤为重要。
👉Deeper Bottleneck Architectures
接下来介绍我们在ImageNet上所使用的更深的网络。Fig5左中所示的结构被称为普通的building block,Fig5右中所示的结构被称为bottleneck building block。深层的非瓶颈残差网络(如Fig5左所示)虽然也能通过增加深度来提升准确率,但是不如瓶颈残差网络经济合算(比如更少的训练耗时)。所以使用瓶颈设计主要是出于实用性的考虑。并且,对于采用瓶颈设计的plain网络,依然存在“退化”现象。瓶颈设计由三个卷积层组成,$1\times 1$卷积层主要用来降维和升维。这样的话,$3\times 3$卷积层的输入和输出维度都比较小。Fig5中的两种设计有着相似的时间复杂度。
三个卷积层的卷积核尺寸按“小大小”排列,形似瓶颈,所以称之为瓶颈设计。
identity shortcuts对瓶颈框架尤为重要。如果将Fig5右中的identity shortcuts换成projection shortcuts,那么时间复杂度和模型大小都将翻倍,因为shortcut的两端维度都很高。因此,对于瓶颈设计,identity shortcuts会使得模型更为高效。
👉👉50-layer ResNet
我们将ResNet-34中的两层block替换成三层瓶颈设计的block,就得到了ResNet-50(见表1)。使用option B升维。
👉👉101-layer and 152-layer ResNets
我们通过使用更多的三层block来构建ResNet-101和ResNet-152。虽然ResNet-152(FLOPs=3.6 billion)深度有了很大的提升,但是FLOPs却比VGG-16/19(FLOPs=15.3/19.6 billion)还低。
ResNet-50/101/152比ResNet-34的准确率高很多(见表3和表4)。从表3和表4中都能发现,对于ResNet,深度越深,模型准确率越高,并没有发生“退化”现象。
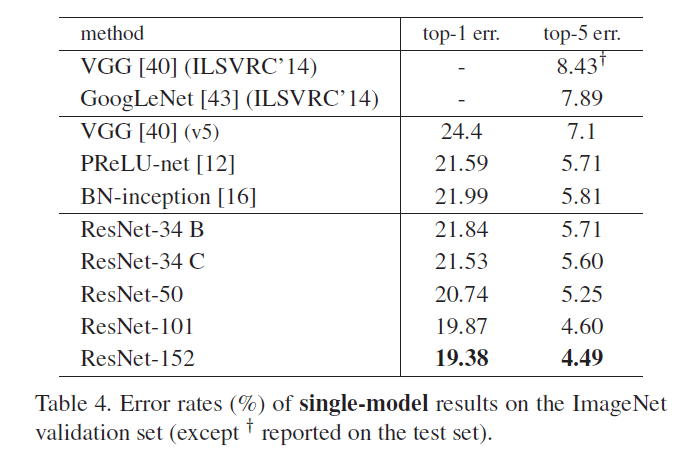
Comparisons with State-of-the-art Methods
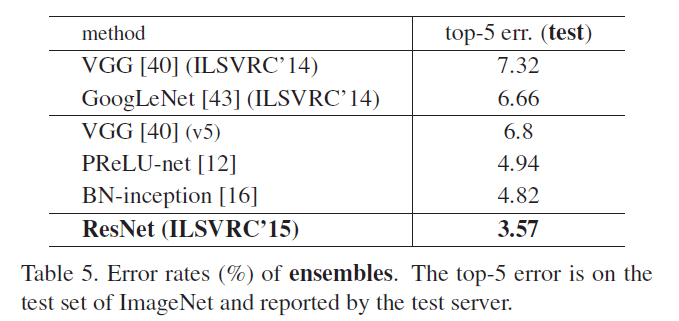
在表4中,我们对比了以前最优的单模型结果。我们的baseline(即ResNet-34)就已经取得了很好的结果。ResNet-152的top-5错误率仅有4.49%,这一单模型结果比表5中其他组合模型的结果还要好。在表5中,我们组合了6个不同深度的ResNet模型(只包含两个ResNet-152)。最终ResNet组合模型的top-5错误率为3.57%,取得了ILSVRC 2015第一名的成绩。
4.2.CIFAR-10 and Analysis
我们在CIFAR-10数据集上进行了更多的研究。在训练集上进行训练,在测试集上进行评估。本部分主要集中在对极深网络的研究,而不是着重于取得更优的结果,所以接下来会使用尽可能简单的框架。
plain网络和ResNet分别使用Fig3中间和右边所示的框架(只是使用类似的框架结构,网络并不完全一样)。网络输入为$32\times 32$的图像,并对每个像素点做了去均值化的处理。网络的构建示意图见下表:
| layer name | output size | 6n+2 layer |
|---|---|---|
| conv 1 | $32\times 32$ | $3\times 3,16$ |
| conv 2_x | $32\times 32$ | $\begin{bmatrix} 3\times 3,16 \\ 3\times 3,16 \ \end{bmatrix} \times 2n$ |
| conv 3_x | $16\times 16$ | $\begin{bmatrix} 3\times 3,32 \\ 3\times 3,32 \ \end{bmatrix} \times 2n$ |
| conv 4_x | $8\times 8$ | $\begin{bmatrix} 3\times 3,64 \\ 3\times 3,64 \ \end{bmatrix} \times 2n$ |
| $1\times 1$ | average pool,10-d fc,softmax |
其中,下采样通过步长为2来进行。网络一共有$6n+2$层,一共有$3n$个shortcuts,且均为identity shortcuts(即option A)。因此,这样构建出来的ResNet和对应的plain网络有着相同的深度,宽度和参数数量。weight decay设为0.0001,momentum设为0.9。权重初始化的方法来自论文“K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In ICCV, 2015.”,使用了BN,没有使用dropout。使用MBGD,mini-batch size=128。使用2块GPU。初始学习率为0.1,在32k和48k迭代时将学习率除以10,总迭代次数为64k(基于45k训练集+5k验证集)。我们进行了简单的数据扩展:每个边进行4个像素的padding,然后从padding后的图像中随机截取$32\times 32$大小的图像或者其水平翻转作为输入。测试阶段,我们仅使用原始的$32\times 32$大小的图像,没有其他额外处理。
我们比较了$n=\{ 3,5,7,9 \}$,分别能得到20,32,44,56层的网络。Fig6左展示了plain网络的表现。虚线为训练误差,粗线为测试误差。从Fig6左中可以看出,越深的plain网络却有着更高的训练误差。这一现象和在ImageNet以及MNIST数据集上测试的结果相似。
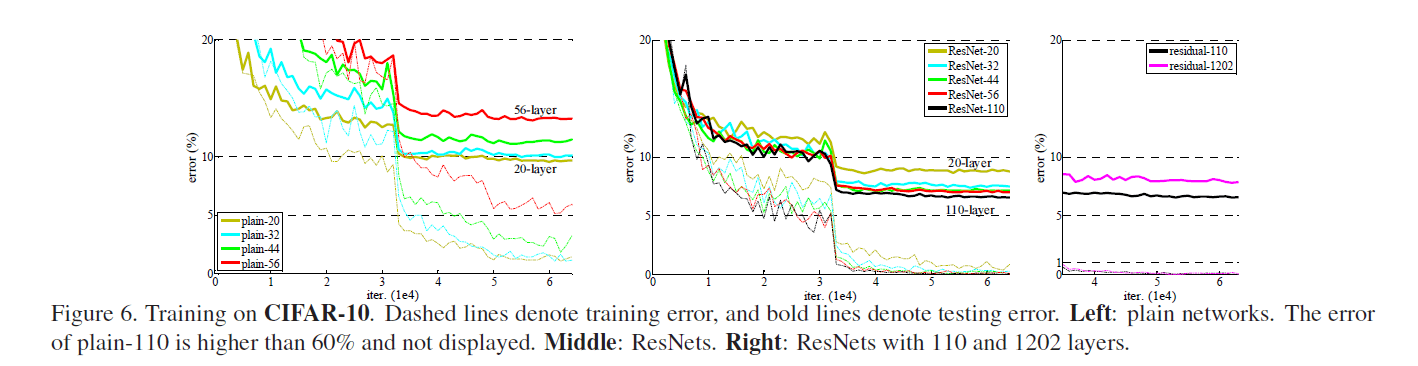
Fig6中间的图展示了ResNet的表现。深度越深,准确率越高,解决了“退化”问题。
我们进一步探索了$n=18$,即110层的ResNet。此时,我们发现初始学习率设为0.1有点偏大(收敛有点慢,不过最后也能达到相近的准确率)。因此,我们将初始学习率设为了0.01,当训练误差低于80%(大约400次迭代)时,将学习率重新改为0.1,然后按照之前的策略继续训练。110层的ResNet收敛的非常好,见Fig6中间。并且相比FitNet和Highway,其参数更少,准确率更高,见表6。
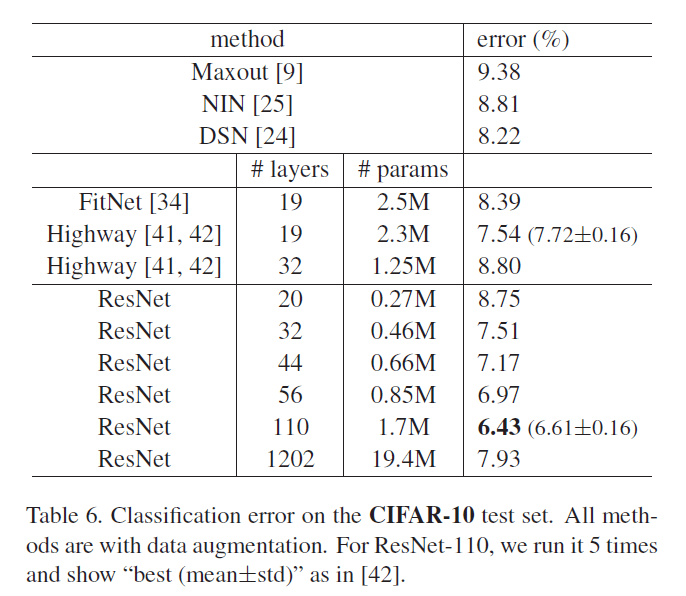
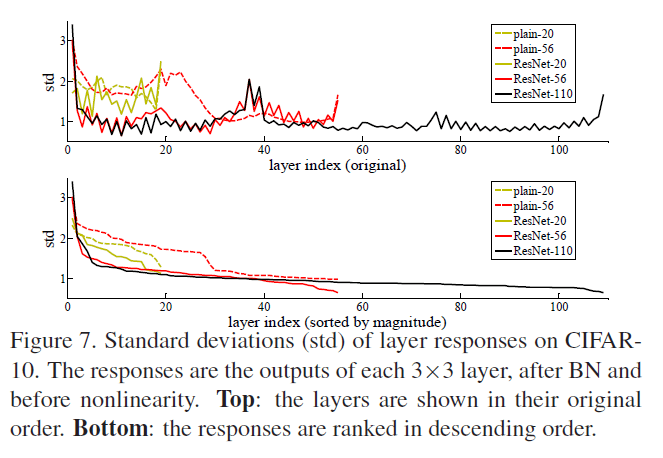
👉Analysis of Layer Responses
Fig7展示了在CIFAR-10数据集上layer responses的标准差。reponses指的是$3\times 3$层的输出,在BN之后,非线性(比如ReLU激活函数)之前。对于ResNet,这种分析揭示了残差函数的reponse强度。Fig7显示ResNet通常比对应的plain网络的reponse要小。这个结果也印证了我们在第3.1部分的讨论:残差函数相比非残差函数更接近零。并且我们还注意到,ResNet越深,response越小。当层数变多时,ResNet中的每一层仅对signal做微小的修改。
👉Exploring Over 1000 layers
使$n=200$,得到了1202层的网络。我们的方法依然奏效,没有遇到优化困难。该网络的训练误差小于0.1%(见Fig6右),测试误差也相当不错(7.93%,见表6)。
尽管ResNet-1202和ResNet-110有着相近的训练误差,但是ResNet-1202的测试误差却比ResNet-110的测试误差要高。我们认为是过拟合导致的。对于CIFAR-10这个小型数据集,ResNet-1202有点太大了,很容易出现过拟合。在CIFAR-10数据集上取得最优结果的框架,都应用了一些强壮的正则化方法(例如maxout或dropout)以获得最优的结果,但我们没有用这些正则化方法,我们只是focus在优化困难这一问题上。但是如果我们的框架也添加了这些正则化方法,结果可能会更好,这个有待进一步研究。
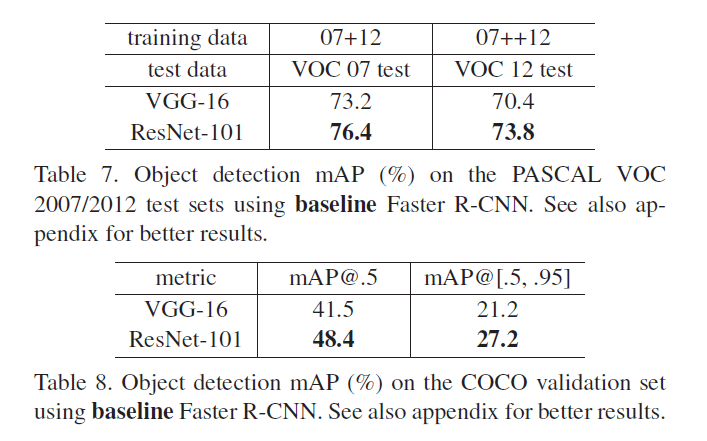
4.3.Object Detection on PASCAL and MS COCO
我们的方法在其他识别任务中也有不错的表现。表7和表8展示了基于PASCAL VOC 2007/2012和COCO数据集的目标检测结果。我们采用Faster R-CNN作为检测方法,将其中的VGG-16替换为了ResNet-101。
5.原文链接
👽Deep Residual Learning for Image Recognition