本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.轮廓检测
轮廓检测:【OpenCV基础】第二十六课:轮廓发现。
2.道格拉斯-普克算法
拉默-道格拉斯-普克算法(Ramer–Douglas–Peucker algorithm),又称道格拉斯-普克算法(Douglas–Peucker algorithm)和迭代端点拟合算法(iterative end-point fit algorithm),是一种将线段组成的曲线降采样为点数较少的类似曲线的算法。它是最早成功地用于制图综合的算法之一。
简称为RDP算法或DP算法。
2.1.算法思路
该算法的目的是,给定一条由线段构成的曲线(在某些情况下也称为折线),找到一条点数较少的相似曲线。该算法根据原曲线与简化曲线之间的最大距离(即曲线之间的豪斯多夫距离)来定义“不相似”。简化曲线由定义原始曲线的点的子集组成。
2.2.算法流程
起始曲线是一组有序的点或线,距离维度$\epsilon > 0$。
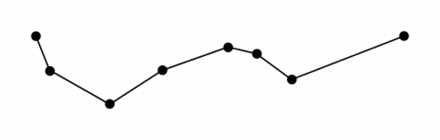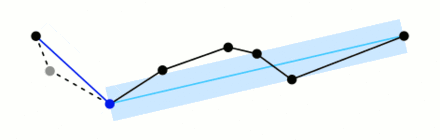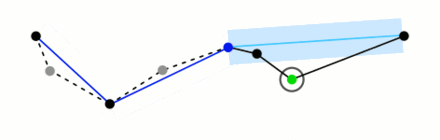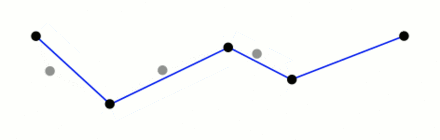
该算法递归划分线。最初,它被赋予了第一点和最后一点之间的所有点。它自动标记要保留的第一点和最后一点。然后它找到离以第一点和最后一点为终点的线段最远的点;这个点显然是曲线上离终点之间的近似线段最远的点。如果这个点离线段的距离比$\epsilon$更近,那么在简化曲线不比$\epsilon$差的情况下,可以舍弃任何当前没有标记保留的点。
如果离线段最远的点大于近似值$\epsilon$,那么该点必须保留。该算法以第一点和最远点递归调用自身,然后以最远点和最后一点调用自身,其中包括最远点被标记为保留。
当递归完成后,可以生成一条新的输出曲线,该曲线由所有且仅由那些被标记为保留的点组成。
2.3.cv::approxPolyDP
1
2
3
4
5
6
void approxPolyDP(
InputArray curve,
OutputArray approxCurve,
double epsilon,
bool closed
);
本API即使用RDP算法。参数详解:
InputArray curve:即2.1.2部分的起始曲线。OutputArray approxCurve:即2.1.2部分简化后的曲线。double epsilon:即2.1.2部分的阈值$\epsilon$。bool closed:如果为true,则简化后的曲线闭合(即起始点和终止点相连)。否则为false。
3.轮廓周围绘制矩形
3.1.cv::boundingRect
1
2
3
Rect boundingRect(
InputArray array
);
得到轮廓周围最小外接矩形。

3.2.cv::minAreaRect
1
2
3
RotatedRect minAreaRect(
InputArray points
);
得到轮廓周围最小外接旋转矩形。

4.轮廓周围绘制圆和椭圆
4.1.cv::minEnclosingCircle
1
2
3
4
5
void minEnclosingCircle(
InputArray points,
CV_OUT Point2f& center,
CV_OUT float& radius
);
该API用于在轮廓周围绘制最小圆,参数详解:
InputArray points:输入的点集,比如一个区域、轮廓等。Point2f& center:圆心位置。float& radius:圆的半径。

4.2.cv::fitEllipse
1
2
3
RotatedRect fitEllipse(
InputArray points
);
该API用于在轮廓周围绘制最小椭圆。
