本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.图像矩
矩是概率与统计中的一个概念,是随机变量的一种数字特征。详细解释请见:随机变量的矩。
图像的矩(image moments)主要表征了图像区域的几何特征,又称为几何矩,由于其具有旋转、平移、尺度等特性的不变特征,所以又称其为不变矩。
M.K.Hu在1961年首先提出了不变矩的概念。1979年M.R.Teague根据正交多项式理论提出了Zernike矩。本文主要介绍Hu矩。
2.Hu矩
一幅$M\times N$的数字图像$f(i,j)$,其$p+q$阶几何矩$m_{pq}$和中心矩$\mu_{pq}$为:
\[m_{pq}=\sum^M_{i=1} \sum^N_{j=1} i^p j^q f(i,j)\] \[\mu_{pq}=\sum^M_{i=1} \sum^N_{j=1} (i-\bar{i})^p (j-\bar{j})^q f(i,j)\]其中$f(i,j)$为图像在坐标点$(i,j)$处的灰度值。且有:
\[\bar{i}=\frac{m_{10}}{m_{00}}, \bar{j}=\frac{m_{01}}{m_{00}}\]若将$m_{00}$看作是图像的灰度质量,则$(\bar{i},\bar{j})$为图像的质心坐标,那么中心矩$\mu_{pq}$反映的是图像灰度相对于其灰度质心的分布情况。可以用几何矩来表示中心矩,0~3阶中心矩与几何矩的关系如下:
\[\mu_{00} = m_{00}\] \[\mu_{10} = 0\] \[\mu_{01} = 0\] \[\mu_{11}=m_{11}-\bar{y} m_{10}\] \[\mu_{20}=m_{20}-\bar{y} m_{01}\] \[\mu_{02}=m_{02}-\bar{y} m_{01}\] \[\mu_{30}=m_{30}-2\bar{x}m_{20}+2\bar{x}^2 m_{10}\] \[\mu_{12}=m_{12}-2\bar{y}m_{11}-\bar{x}m_{02}+2\bar{y}^2m_{10}\] \[\mu_{21}=m_{21}-2\bar{x}m_{11}-\bar{y}m_{20}+2\bar{x}^2m_{01}\] \[\mu_{03}=m_{03} - 2\bar{y}m_{02} + 2\bar{y}^2 m_{01}\]为了抵消尺度变化对中心矩的影响,利用0阶中心矩$\mu_{00}$对各阶中心矩进行归一化处理,得到归一化中心矩:
\[\eta_{pq} = \frac{\mu_{pq}}{\mu_{00}^{\gamma}}, \ (\gamma=\frac{p+q}{2},p+q=2,3,...)\]利用二阶和三阶归一化中心矩可以导出下面7个不变矩组,它们在图像平移、旋转和比例变化时保持不变:
\[\Phi_1=\eta_{20}+\eta_{02}\] \[\Phi_2=(\eta_{20}-\eta_{02})^2+4\eta_{11}^2\] \[\Phi_3=(\eta_{20}-3\eta_{12})^2+3(\eta_{21}-\eta_{03})^2\] \[\Phi_4=(\eta_{30}+\eta_{12})^2+(\eta_{21}+\eta_{03})^2\] \[\Phi_5=(\eta_{30}+3\eta_{12})(\eta_{30}+\eta_{12})[(\eta_{30}+\eta_{12})^2-3(\eta_{21}+\eta_{03})^2]+(3\eta_{21}-\eta_{03})(\eta_{21}+\eta_{03})[3(\eta_{30}+\eta_{12})^2-(\eta_{21}+\eta_{03})^2]\] \[\Phi_6=(\eta_{20}-\eta_{02})[(\eta_{30}+\eta_{12})^2 - (\eta_{21}+\eta_{03})^2]+4\eta_{11}(\eta_{30}+\eta_{12})(\eta_{21}+\eta_{03})\] \[\Phi_7=(3\eta_{21}-\eta_{03})(\eta_{30}+\eta_{12})[(\eta_{30}+\eta_{12})^2 - 3(\eta_{21}+\eta_{03})^2]+(3\eta_{12}-\eta_{30})(\eta_{21}+\eta_{03})[3(\eta_{30}+\eta_{12})^2-(\eta_{21}+\eta_{03})^2]\]3.相关API
3.1.cv::moments
1
2
3
4
Moments moments(
InputArray array,
bool binaryImage = false
);
该API用于计算图像的中心矩(1阶、2阶、3阶)、几何矩(2阶、3阶)和归一化几何矩(2阶、3阶)。参数详解:
InputArray array:输入图像。bool binaryImage:是否对图像进行二值化处理。如果为true,则所有非0像素会被视为1。
Moments类的定义:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class CV_EXPORTS_W_MAP Moments
{
public:
//! the default constructor
Moments();
//! the full constructor
Moments(double m00, double m10, double m01, double m20, double m11,
double m02, double m30, double m21, double m12, double m03 );
////! the conversion from CvMoments
//Moments( const CvMoments& moments );
////! the conversion to CvMoments
//operator CvMoments() const;
//! @name spatial moments
//! @{
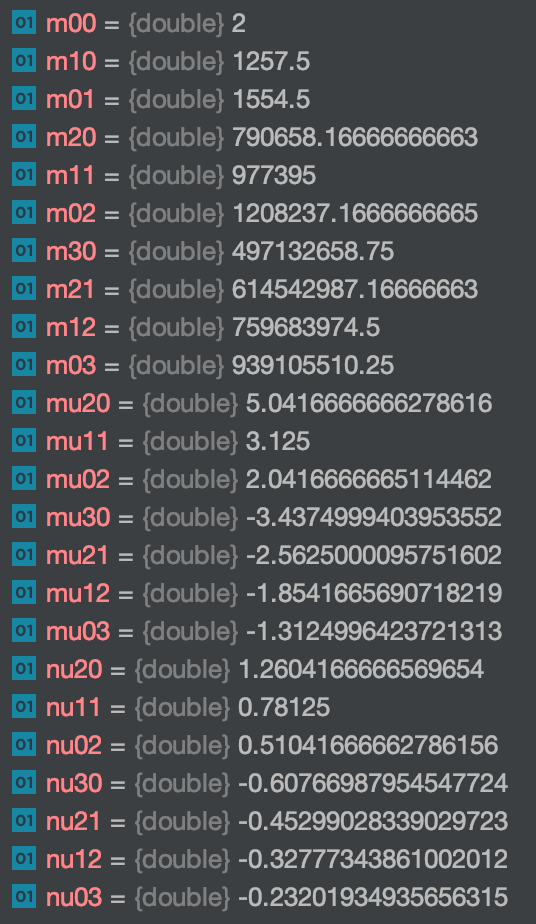
CV_PROP_RW double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
//! @}
//! @name central moments
//! @{
CV_PROP_RW double mu20, mu11, mu02, mu30, mu21, mu12, mu03;
//! @}
//! @name central normalized moments
//! @{
CV_PROP_RW double nu20, nu11, nu02, nu30, nu21, nu12, nu03;
//! @}
};
3.2.cv::HuMoments
1
2
3
4
void HuMoments(
const Moments& moments,
double hu[7]
);
参数详解:
const Moments& moments:输入cv::moments算出来的矩。double hu[7]:输出第2部分中的$\Phi_1 \sim \Phi_7$。
3.3.cv::contourArea
1
2
3
4
double contourArea(
InputArray contour,
bool oriented = false
);
该API用于计算轮廓围成的面积。参数详解:
InputArray contour:输入的轮廓。bool oriented:如果为true,则返回带正负号的面积值,正负取决于轮廓的方向(顺时针或逆时针)。如果为false,则返回面积的绝对值。
3.4.cv::arcLength
1
2
3
4
double arcLength(
InputArray curve,
bool closed
);
该API用于计算曲线的长度或者闭合轮廓的周长。参数详解:
InputArray curve:输入曲线。bool closed:曲线是否闭合。