本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
本博文只介绍原文第2部分:使用弹性形变来扩展图像数据。如对全文感兴趣,请移步至全文链接。
2.Expanding Data Sets through Elastic Distortions
通过应用变换(transformations)来生成额外的数据,促使算法学习到变换不变性(transformation invariance)。
接下来介绍弹性形变的过程。首先针对原始图像中的每个像素点都生成一个位移量,所有像素点的位移量便构成一个位移场(the displacement field)。例如我们可以用$?x(x,y) =1 , ?y(x,y)=0$表示将像素点$(x,y)$向右平移一个单位。
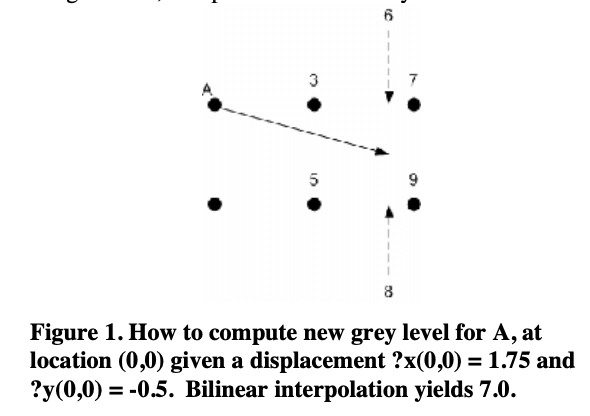
以Fig1为例,解释下如何计算每个像素点上新的灰度值。在Fig1中,假设A点的坐标为$(0,0)$,则对应的3,7,5,9的坐标分别为$(1,0),(2,0),(1,-1),(2,-1)$。假设A点的位移量为$?x(0,0)=1.75,?y(0,0)=-0.5$,如图中箭头所示。此时使用双线性插值,尽管这里也可以使用其他的插值方法,但双线性插值是最简单的并且对于我们所用的$29 \times 29$分辨率的图像数据效果还不错。首先进行水平方向上的插值:$3+0.75\times (7-3)=6,5+0.75\times (9-5)=8$。然后进行垂直方向上的插值:$8+0.5\times (6-8)=7$。因此,A点新的像素值为7。如果位移后的位置超出了图像范围,则赋成背景的像素值(比如0)。
然后介绍下如何生成位移场,针对每个像素点都有$?x(x,y)=rand(-1,+1),?y(x,y)=rand(-1,+1)$,$rand(-1,+1)$表示在-1到+1的范围内随机均匀取值。然后对这个位移场施加一个高斯模糊(标准差为$\sigma$)。

在Fig2中,左上为原图,右上使用了较小的$\sigma$,左下和右下使用了较大的$\sigma$。
最后,对于平滑后的位移场(a smoothed random field)再乘上一个$\alpha$得到最终的位移场。根据这个最终的位移场,通过双线性插值来更新每个像素点的像素值得到弹性形变后的图像数据。作者使用$\alpha = 8$。
3.原文链接
👽Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis