【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.低维嵌入
在高维情形下出现的数据样本稀疏、距离计算困难等问题,是所有机器学习方法共同面临的严重障碍,被称为“维数灾难”(curse of dimensionality)。
缓解维数灾难的一个重要途径是降维(dimension reduction),亦称“维数约简”,即通过某种数学变换将原始高维属性空间转变为一个低维“子空间”(subspace),在这个子空间中样本密度大幅提高,距离计算也变得更为容易。为什么能进行降维?这是因为在很多时候,人们观测或收集到的数据样本虽是高维的,但与学习任务密切相关的也许仅是某个低维分布,即高维空间中的一个低维“嵌入”(embedding)。下图给出了一个直观的例子。原始高维空间中的样本点,在这个低维嵌入子空间中更容易进行学习。
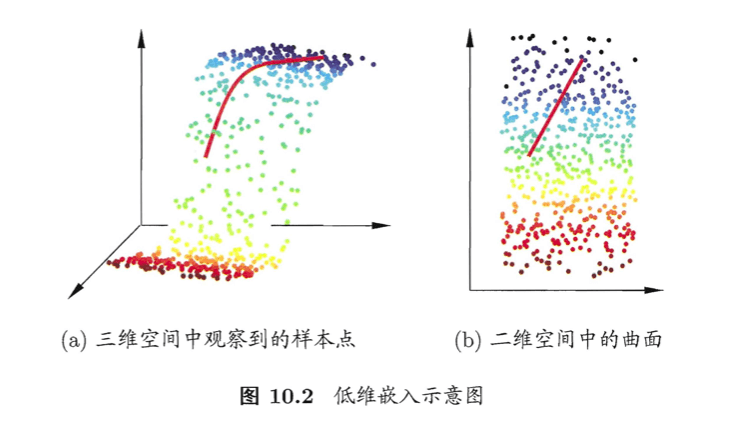
如上图所示,若要求原始空间中样本之间的距离在低维空间中得以保持,我们可以使用一种经典的降维方法,为“多维缩放”(Multiple Dimensional Scaling,简称MDS)。下面简单介绍一下这个方法。
假定$m$个样本在原始空间的距离矩阵为$\mathbf{D} \in \mathbb{R} ^{m\times m}$,其第$i$行$j$列的元素$dist_{ij}$为样本$\mathbf{x}_i$到$\mathbf{x}_j$的距离。我们的目标是获得样本在$d’$维空间的表示$\mathbf{Z} \in \mathbb{R} ^{d’ \times m}, d’ \leqslant d$,且任意两个样本在$d’$维空间中的欧式距离等于原始空间中的距离,即$\parallel z_i - z_j \parallel = dist_{ij}$。
令$\mathbf{B} = \mathbf{Z}^T \mathbf{Z} \in \mathbb{R} ^{m\times m}$,其中$\mathbf{B}$为降维后样本的内积矩阵,$b_{ij} = z_i ^T z_j$,有
\[\begin{align} dist_{ij}^2 &= \parallel z_i \parallel^2 + \parallel z_j \parallel ^2 - 2 z_i ^T z_j \\&= b_{ii} + b_{jj} - 2b_{ij} \end{align} \tag{1}\]为便于讨论,令降维后的样本$\mathbf{Z}$被中心化,即$\sum_{i=1}^m z_i =0$。显然,矩阵$\mathbf{B}$的行与列之和均为零,即$\sum_{i=1}^m b_{ij} = \sum_{j=1}^m b_{ij} = 0$。易知
\[\begin{align} \sum_{i=1}^m dist_{ij}^2 &= \sum_{i=1}^m (b_{ii}+b_{jj} - 2b_{ij}) \\& = \sum_{i=1}^m b_{ii} + \sum_{i=1}^m b_{jj} -2\sum_{i=1}^m b_{ij} \\&= tr(\mathbf{B}) + m b_{jj} \end{align} \tag{2}\] \[\sum_{j=1}^m dist_{ij}^2 = tr(\mathbf{B})+m b_{ii} \tag{3}\] \[\sum_{i=1}^m \sum_{j=1}^m dist_{ij}^2 = 2m tr(\mathbf{B}) \tag{4}\]其中$tr(\cdot)$表示矩阵的迹(trace),$tr(\mathbf{B})=\sum_{i=1}^m \parallel z_i \parallel ^2$。令
\[dist_{i\cdot}^2 = \frac{1}{m} \sum_{j=1}^m dist_{ij}^2 \tag{5}\] \[dist_{\cdot j}^2 = \frac{1}{m} \sum_{i=1}^m dist_{ij}^2 \tag{6}\] \[dist_{\cdot \cdot}^2 = \frac{1}{m^2} \sum_{i=1}^m \sum_{j=1}^m dist_{ij}^2 \tag{7}\]由式(1)和式(2)~(7)可得
\[\begin{align} b_{ij} &= -\frac{1}{2}(dist_{ij}^2 -b_{ii}-b_{jj}) \\&= -\frac{1}{2} (dist_{ij}^2 -dist_{i\cdot}^2 - dist_{\cdot j}^2 + dist_{\cdot \cdot}^2 ) \end{align} \tag{8}\]由此即可通过降维前后保持不变的距离矩阵$\mathbf{D}$求取内积矩阵$\mathbf{B}$。
对矩阵$\mathbf{B}$做特征值分解(eigenvalue decomposition,见本文第2部分),$\mathbf{B} = \mathbf{V} \Lambda \mathbf{V}^T$,其中$\Lambda = \text{diag} (\lambda_1,\lambda_2,…,\lambda_d)$为特征值构成的对角矩阵,$\lambda_1 \geqslant \lambda_2 \geqslant \cdots \geqslant \lambda_d$,$\mathbf{V}$为特征向量矩阵。假定其中有$d^*$个非零特征值,它们构成对角矩阵$\Lambda_* = \text{diag} (\lambda_1 , \lambda_2 , … , \lambda_{d^*})$,令$\mathbf{V}_*$表示相应的特征向量矩阵,则$\mathbf{Z}$可表达为
\[\mathbf{Z} = \Lambda_*^{1/2} \mathbf{V}_*^T \in \mathbb{R} ^{d^* \times m} \tag{9}\]式(9)的推导见本文第3部分。
在现实应用中为了有效降维,往往仅需降维后的距离与原始空间中的距离尽可能接近,而不必严格相等。此时可取$d’ \ll d$个最大特征值构成对角矩阵$\tilde{\Lambda} = \text{diag} (\lambda_1, \lambda_2,…,\lambda_{d’})$,令$\tilde{\mathbf{V}}$表示相应的特征向量矩阵,则$\mathbf{Z}$可表达为
\[\mathbf{Z} = \tilde{\Lambda}^{1/2} \tilde{\mathbf{V}}^T \in \mathbb{R} ^{d' \times m} \tag{10}\]下面给出MDS算法的描述:
- 输入:距离矩阵$\mathbf{D} \in \mathbb{R}^{m\times m}$,其元素$dist_{ij}$为样本$x_i$到$x_j$的距离;低维空间维数$d’$。
- 过程:
- 根据式(5)~(7)计算$dist_{i\cdot}^2,dist_{\cdot j}^2,dist_{\cdot \cdot}^2$;
- 根据式(8)计算矩阵$\mathbf{B}$;
- 对矩阵$\mathbf{B}$做特征值分解;
- 取$\tilde{\Lambda}$为$d’$个最大特征值所构成的对角矩阵,$\tilde{\mathbf{V}}$为相应的特征向量矩阵。
- 输出:矩阵$\tilde{\mathbf{V}} \tilde{\Lambda} ^{1/2} \in \mathbb{R}^{m\times d’}$,每行是一个样本的低维坐标。
一般来说,欲获得低维子空间,最简单的是对原始高维空间进行线性变换。给定$d$维空间中的样本$\mathbf{X} = (x_1,x_2,…,x_m) \in \mathbb{R}^{d\times m}$,变换之后得到$d’ \leqslant d$(通常令$d’ \ll d$)维空间中的样本:
\[\mathbf{Z} = \mathbf{W}^T \mathbf{X} \tag{11}\]其中$\mathbf{W} \in \mathbb{R}^{d\times d’}$是变换矩阵,$\mathbf{Z} \in \mathbb{R} ^{d’ \times m}$是样本在新空间中的表达。
变换矩阵$\mathbf{W}$可视为$d’$个$d$维基向量,$z_i = \mathbf{W}^T x_i$是第$i$个样本与这$d’$个基向量分别做内积而得到的$d’$维属性向量。换言之,$z_i$是原属性向量$x_i$在新坐标系$\{w_1,w_2,…,w_{d’} \}$中的坐标向量。若$w_i$与$w_j$($i\neq j$)正交,则新坐标系是一个正交坐标系,此时$\mathbf{W}$为正交变换。显然,新空间中的属性是原空间中属性的线性组合。
基于线性变换来进行降维的方法称为线性降维方法,它们都符合式(11)的基本形式,不同之处是对低维子空间的性质有不同的要求,相当于对$\mathbf{W}$施加了不同的约束。
对降维效果的评估,通常是比较降维前后学习器的性能,若性能有所提高则认为降维起到了作用。若将维数降至二维或三维,则可通过可视化技术来直观地判断降维效果。
2.特征值分解
特征值分解简称为EVD,eigenvalue decomposition。设$A_{n \times n}$有$n$个线性无关的特征向量$x_1,…,x_n$,对应特征值分别为$\lambda_1,…,\lambda_n$:
\[A [x_1 \ \cdots \ x_n] = [\lambda_1 x_1 \ \cdots \ \lambda_n x_n]\]所以:
\[A = [x_1\ \cdots \ x_n] \begin{bmatrix} \lambda_1 & \ & \ \\ \ & \ddots & \ \\ \ & \ & \lambda_n \end{bmatrix} [x_1\ \cdots \ x_n] ^{-1}\]因此有特征值分解:
\[AX = X \Lambda\] \[A = X \Lambda X^{-1}\]其中,$X$为$x_1,…,x_n$(特征向量)构成的矩阵,$\Lambda = \text{diag} (\lambda_1,…,\lambda_n)$(特征值从大到小排列)。即使固定$\Lambda$,$X$也不唯一。
当$A$为实对称矩阵的时候,即$A=A^T$,那么它可以被分解成如下的形式:
\[A = P \Lambda P^T\]其中,$P$为正交矩阵。
EVD的前提是$A$得是一个方阵,如果$A$不是方阵,则此时就需要使用奇异值分解(SVD)了。
3.式(9)的推导
因为$d^*$为$\mathbf{V}$的非零特征值,因此$\mathbf{B} = \mathbf{V} \Lambda \mathbf{V}^T$可以写成$\mathbf{B} = \mathbf{V}_* \Lambda_* \mathbf{V}^T_*$(原因见第2部分的讲解),其中$\Lambda_* \in \mathbb{R}^{d\times d}$为$d$个非零特征值构成的特征值对角矩阵,而$\mathbf{V}_* \in \mathbb{R}^{m\times d}$为$\Lambda_* \in \mathbb{R}^{d\times d}$对应的特征向量矩阵,因此有
\[\mathbf{B} = (\mathbf{V}_* \Lambda_*^{1/2}) (\Lambda_*^{1/2} \mathbf{V}_*^T)\]故而$\mathbf{Z} = \Lambda_*^{1/2} \mathbf{V}_*^T \in \mathbb{R} ^{d^* \times m}$。