本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.确定聚类的簇数
我们可以通过WCSS值来选择一个合适的聚类簇数。WCSS的计算如下:
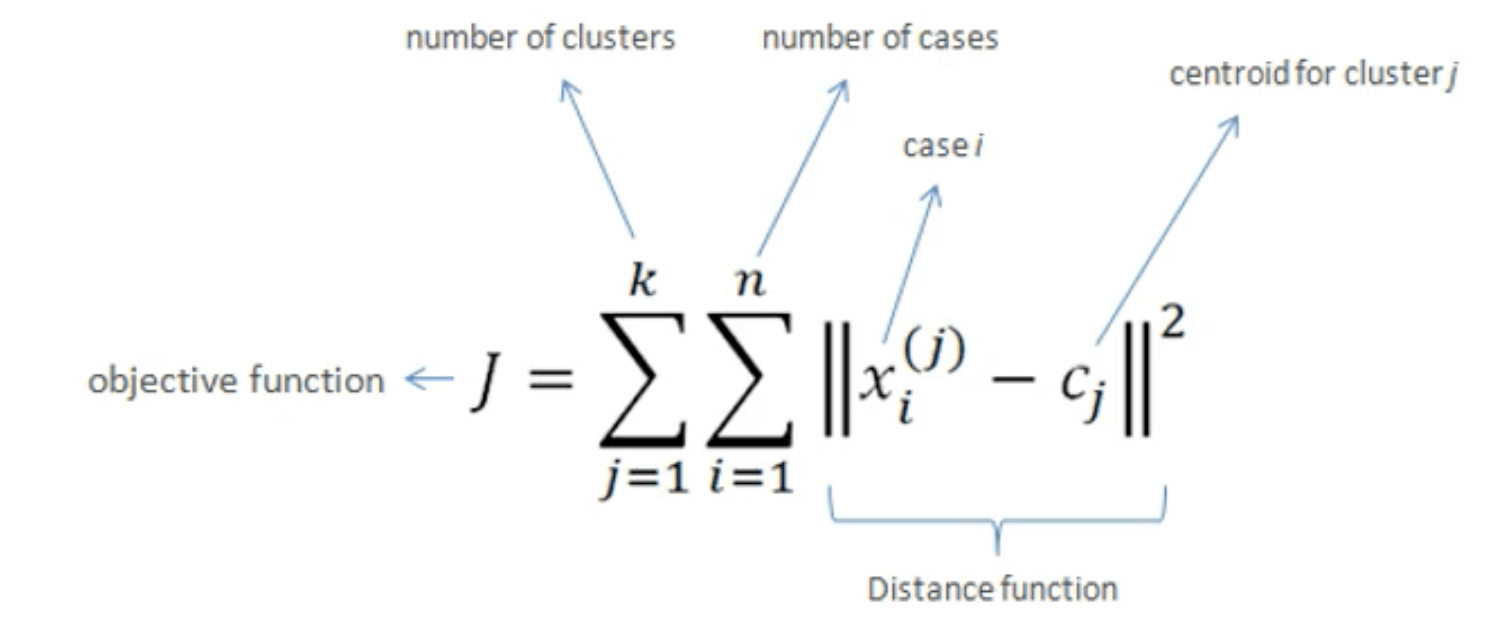
WCSS的特点:聚类的簇数越多,WCSS越低。举个例子,先读入数据:
1
2
3
4
import pandas
dataset = pandas.read_csv("customers.csv")
print(dataset.head())
1
2
3
4
5
6
CustomerID Genre Age Annual Income (k$) Spending Score (1-100)
0 1 Male 19 15 39
1 2 Male 21 15 81
2 3 Female 20 16 6
3 4 Female 23 16 77
4 5 Female 31 17 40
绘制WCSS随着簇数变化的趋势图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
X = dataset.iloc[:, [3, 4]].values
import matplotlib.pyplot as plt
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', random_state=42)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.plot(range(1, 11), wcss)
plt.title("The Elbow Method")
plt.xlabel("Number of clusters")
plt.ylabel("WCSS")
plt.show()
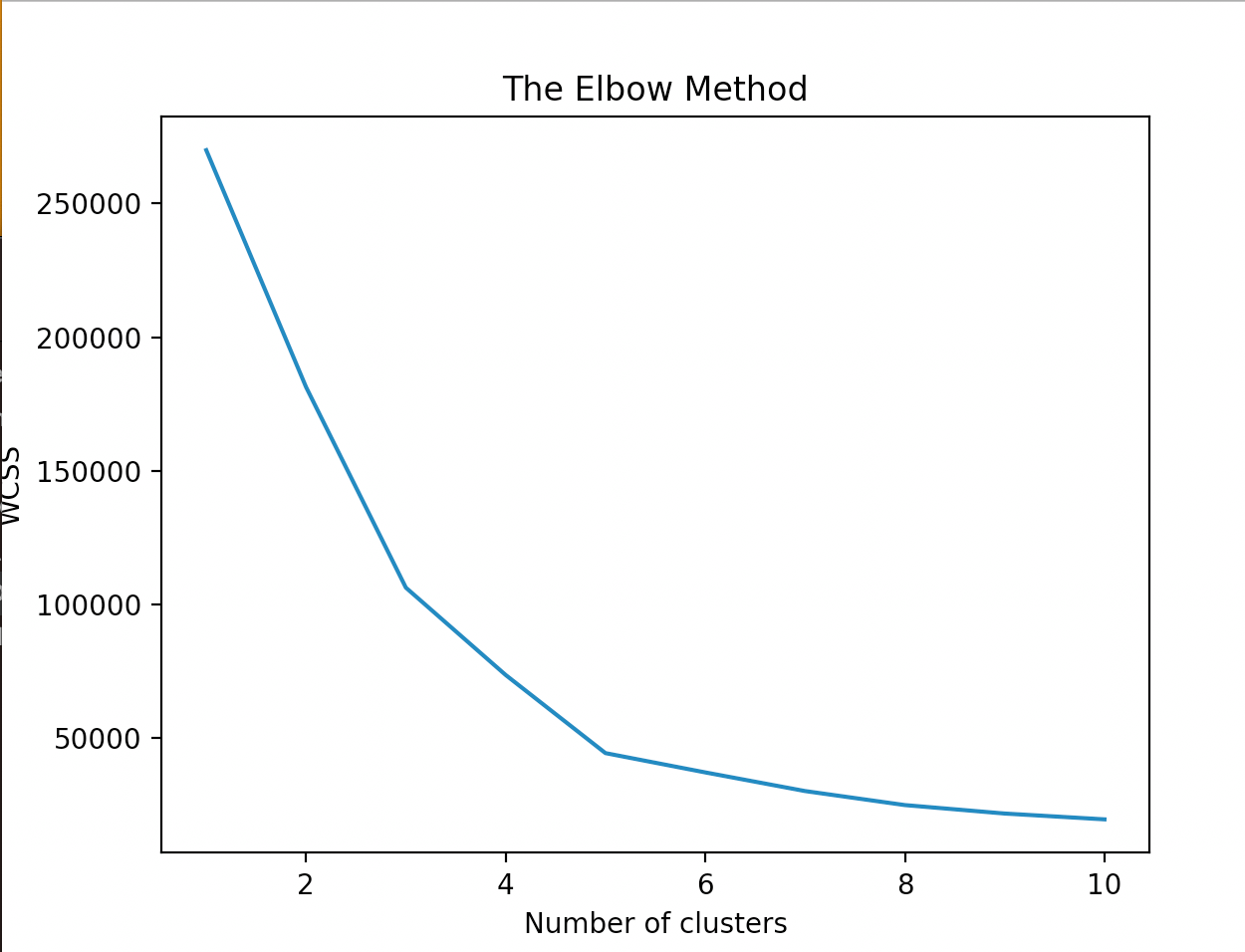
inertia_返回的就是WCSS值。从上图可以看出,当聚类的簇数为5时,WCSS突然下降变缓,我们便可以选择5作为理想的聚类簇数。
KMeans的用法见:【Python基础】第三十八课:使用Python实现k-means聚类。
2.评估聚类效果
\[\text{Silhouette}(x) = \frac{b(x)-a(x)}{\max ([b(x),a(x)])}\]- $a(x)$为样本点$x$到同簇内其他样本点的平均距离。我们希望其越小越好。
- $b(x)$为样本点$x$到异簇中样本点的最小平均距离。我们希望其越大越好。
可以通过以下接口计算Silhouette值:
1
2
from sklearn import metrics
print("Silhouette Coefficient:%0.3f" % metrics.silhouette_score(X, y_kmeans))
绘制Silhouette值随着簇数变化的趋势图:

从上图中可以看出,当簇数为5时,Silhouette值最高。此外,我们也可以使用Silhouette值比较不同的聚类方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
# 比较不同的聚类方法
# ward
ward = AgglomerativeClustering(n_clusters=5, affinity="euclidean", linkage="ward")
y_ward = ward.fit_predict(X)
# complete
complete = AgglomerativeClustering(n_clusters=5, affinity="euclidean", linkage="complete")
y_complete = complete.fit_predict(X)
# kmeans
kmeans = KMeans(n_clusters=5, init="k-means++", random_state=42)
y_kmeans = kmeans.fit_predict(X)
for est, title in zip([y_ward, y_complete, y_kmeans], ['ward', 'complete', 'kmeans']):
print(title, metrics.silhouette_score(X, est))
1
2
3
ward 0.5529945955148897
complete 0.5529945955148897
kmeans 0.553931997444648
AgglomerativeClustering的用法见:【Python基础】第三十七课:使用Python实现层次聚类。
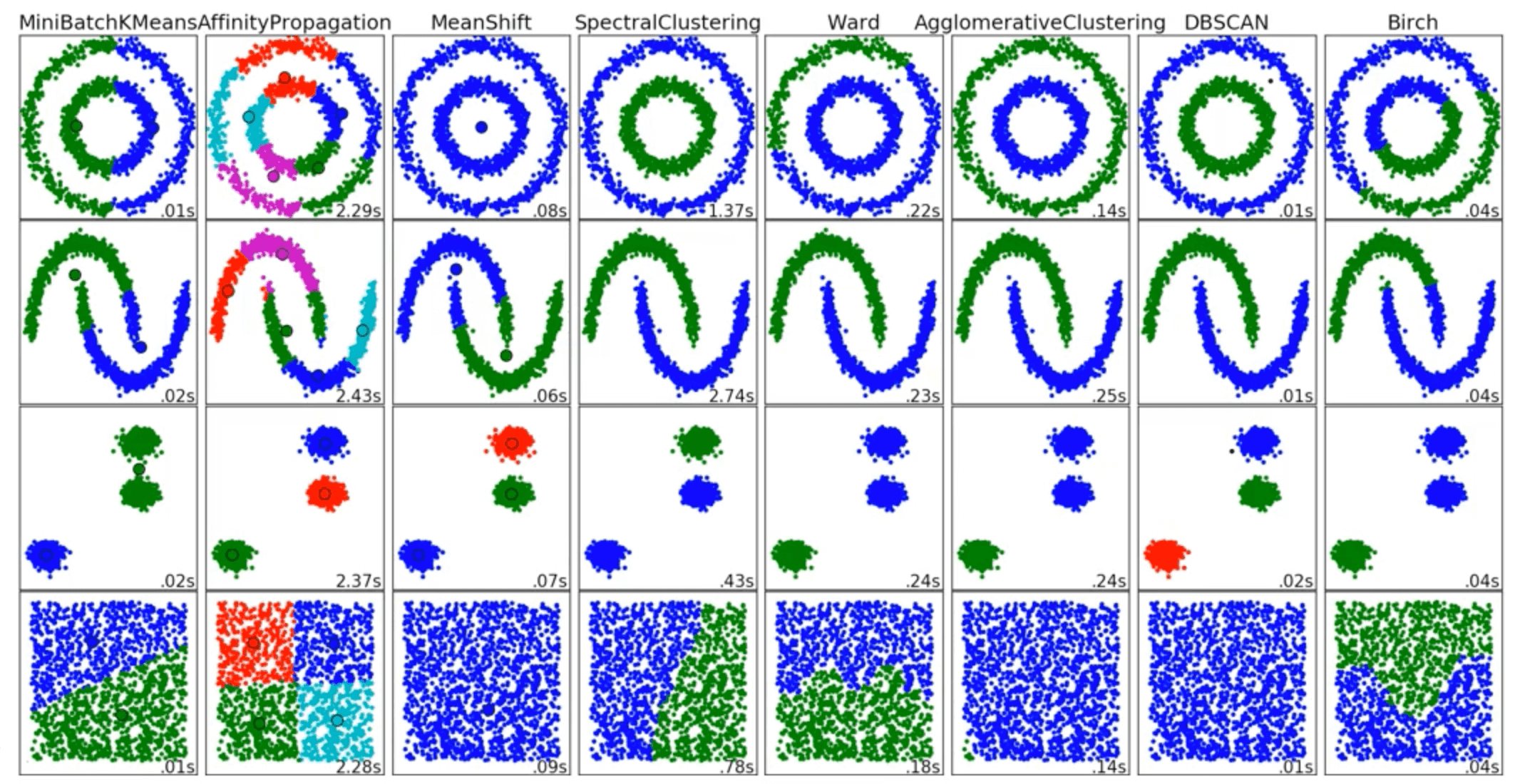
不同的聚类方法适用于不同分布的数据: