本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.概念解释
在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到,这个求解参数的过程就称之为相机标定(或摄像机标定)。无论是在图像测量或者机器视觉应用中,相机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此,做好相机标定是做好后续工作的前提,提高标定精度是科研工作的重点所在。
2.相关术语
👉焦点,在几何光学中有时也称为像点,是源头的光线经过物镜后汇聚的点。
👉焦距,也称为焦长,是光学系统中衡量光的聚集或发散的度量方式,指从透镜中心到光聚集之焦点的距离。亦是照相机中,从镜片光学中心到底片、CCD或CMOS等成像平面的距离。
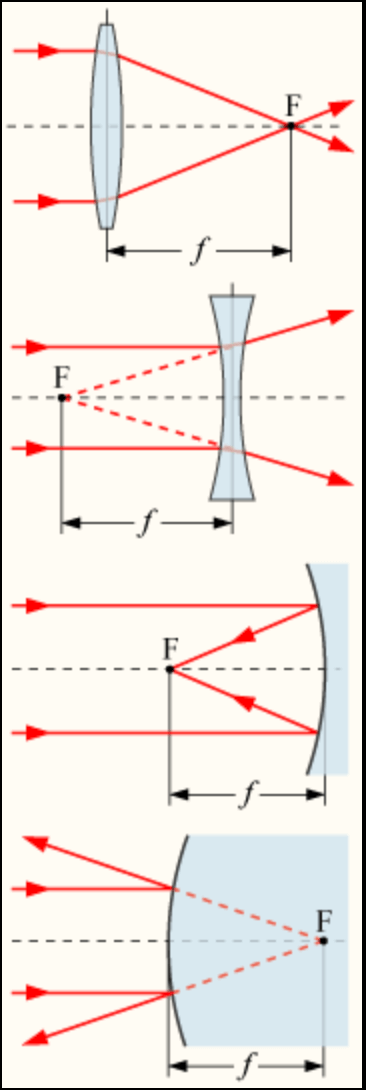
正透镜、负透镜、凹面镜和凸面镜的焦点$F$和焦距$f$:
👉镜头(Lenses)是将拍摄景物在传感器上成像的器件,它通常由几片透镜、光圈叶片、对焦马达等光学元件组成。
👉传感器(Sensor)是摄像头组成的核心,其作用是作为相机的感光元件。摄像头传感器主要有两种,一种是CCD传感器,一种是CMOS传感器,两者区别在于:CCD的优势在于成像质量好,但是由于制造工艺复杂,成本居高不下,特别是大型CCD,价格非常高昂。在相同分辨率下,CMOS价格比CCD便宜,但是CMOS器件产生的图像质量相比CCD来说要低一些。
👉光心:凸透镜近轴光线中,入射线和与其对应且相平行的出射线构成共轭光线,其入射点跟出射点的连线与主光轴的交点,称为凸透镜的焦点,位于透镜中央的点叫光心。
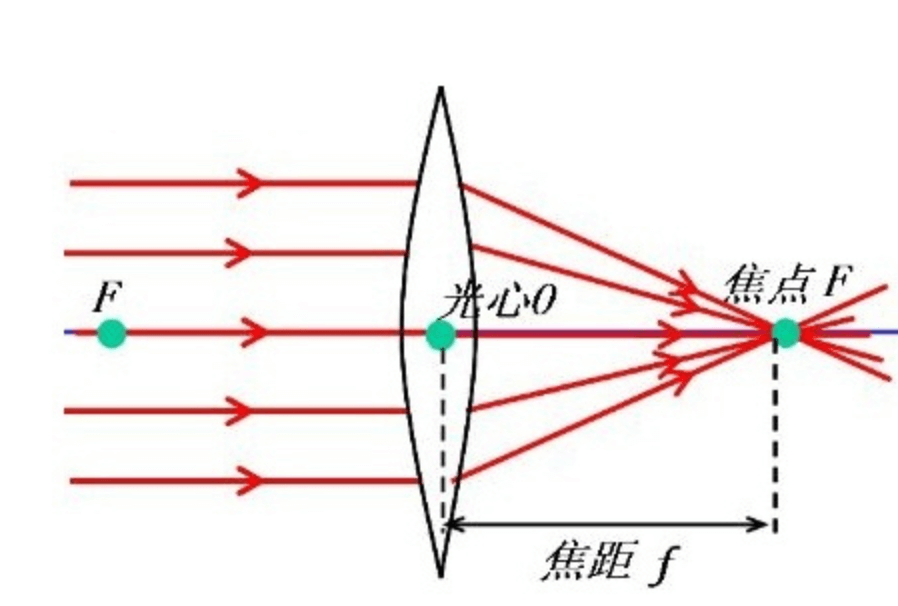
从图中可知,$O$为光心,$F$为焦点。每个透镜主轴上都有一个特殊点,凡是通过该点的光,其传播方向不变,这个点叫光心。经过光心的光线的传播方向不会发生改变。
3.原理介绍
3.1.针孔相机模型
我们通常将相机看成如下所示的透镜模型:
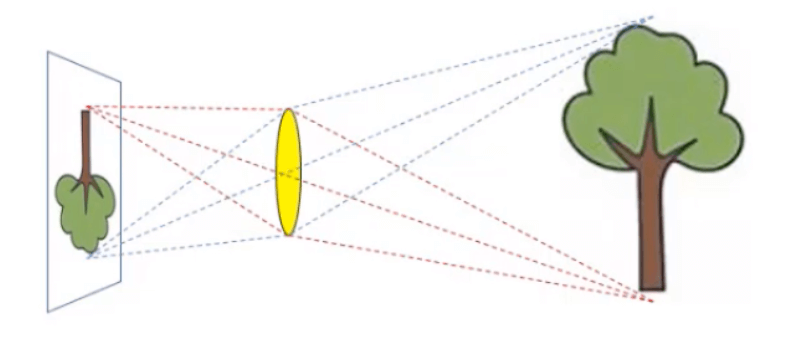
在实际分析时,通常将其简化为针孔模型(小孔成像):

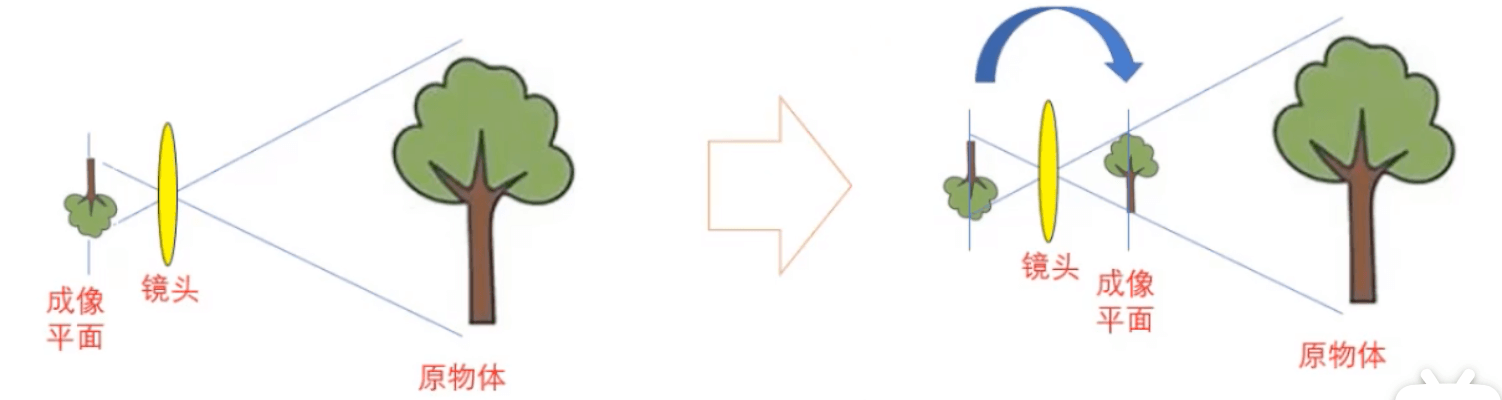
一般为了分析简单,将成像平面画在对称位置,这样图像不再颠倒:
3.2.坐标系介绍
相机标定会用到四个坐标系:
- 世界坐标系:用户定义的三维世界的坐标系,用于描述目标物体在真实世界里的位置。单位通常为米(m)。该坐标系作用于三维空间。
- 相机坐标系:在相机上建立的坐标系,为了从相机的角度描述物体位置而定义,作为沟通世界坐标系和图像/像素坐标系的中间一环。单位通常为米(m)。相机坐标系的原点在光心,其$X_c$、$Y_c$轴分别与像面的两边平行,其$Z_c$轴与光轴重合,且垂直于图像坐标系平面并通过图像坐标系的原点,相机坐标系与图像坐标系之间的距离为焦距$f$。该坐标系作用于三维空间。
- 图像坐标系:为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入,方便进一步得到像素坐标系下的坐标。其原点是相机光轴与像面的交点(称为主点),即图像的中心点。其$x,y$轴和像素坐标系的$u,v$轴平行,故图像坐标系和像素坐标系实际是平移关系。单位通常为毫米(mm)。该坐标系作用于二维空间。
- 像素坐标系:为了描述物体成像后的像点在数字图像上(相片)的坐标而引入,是我们真正从相机内读取到的信息所在的坐标系。单位为像素。像素坐标平面和图像坐标平面重合,但像素坐标系原点位于图像左上角。该坐标系作用于二维空间。
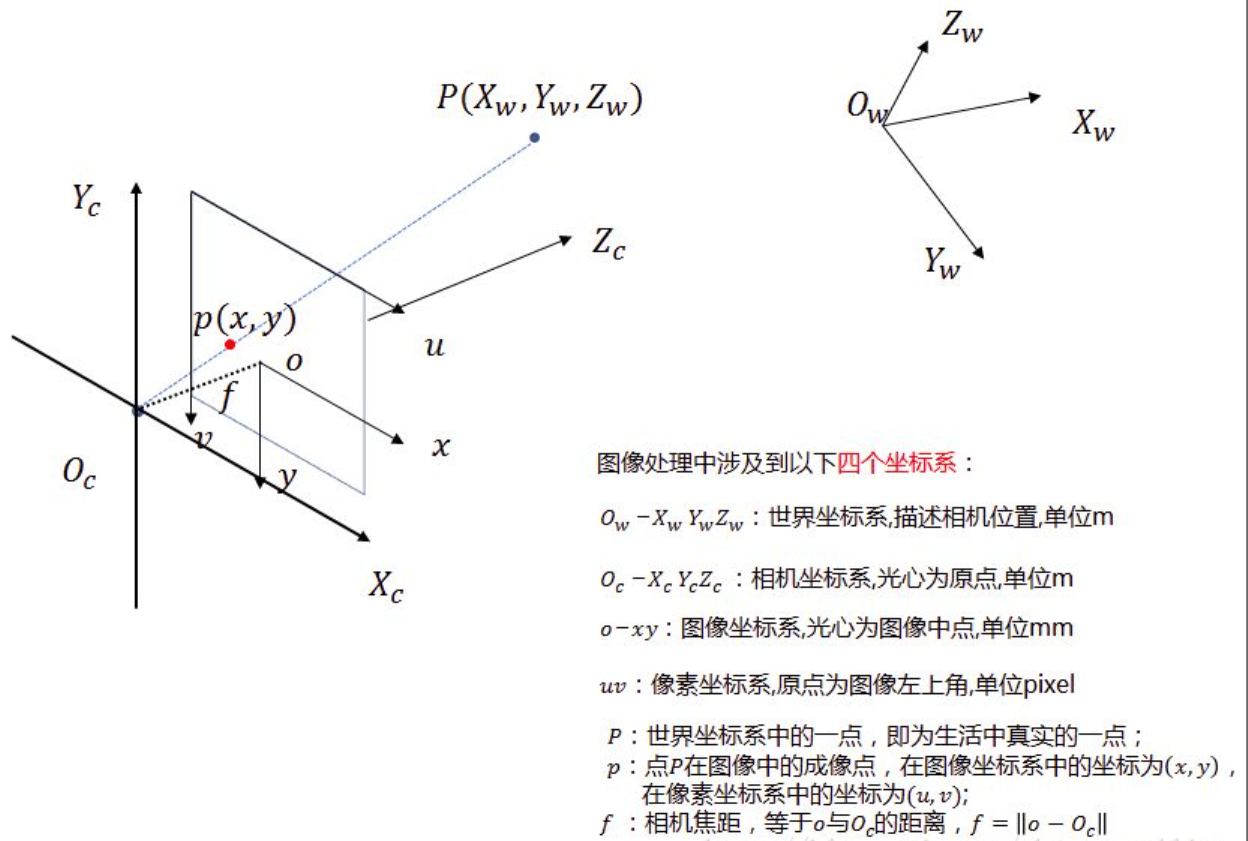
3.3.相机外参
首先考虑一个问题,如何将世界坐标系中的点映射到相机坐标系?其实相机坐标系可以看作是世界坐标系通过刚体变换(旋转+平移)得到的。
刚体变换能够保持物体中各点的距离和角度。常见的刚体变换有平移、旋转和镜像。
我们先只考虑旋转,假设将坐标系以$X$轴为中心进行旋转,即$X$不变,旋转$Y-Z$平面:
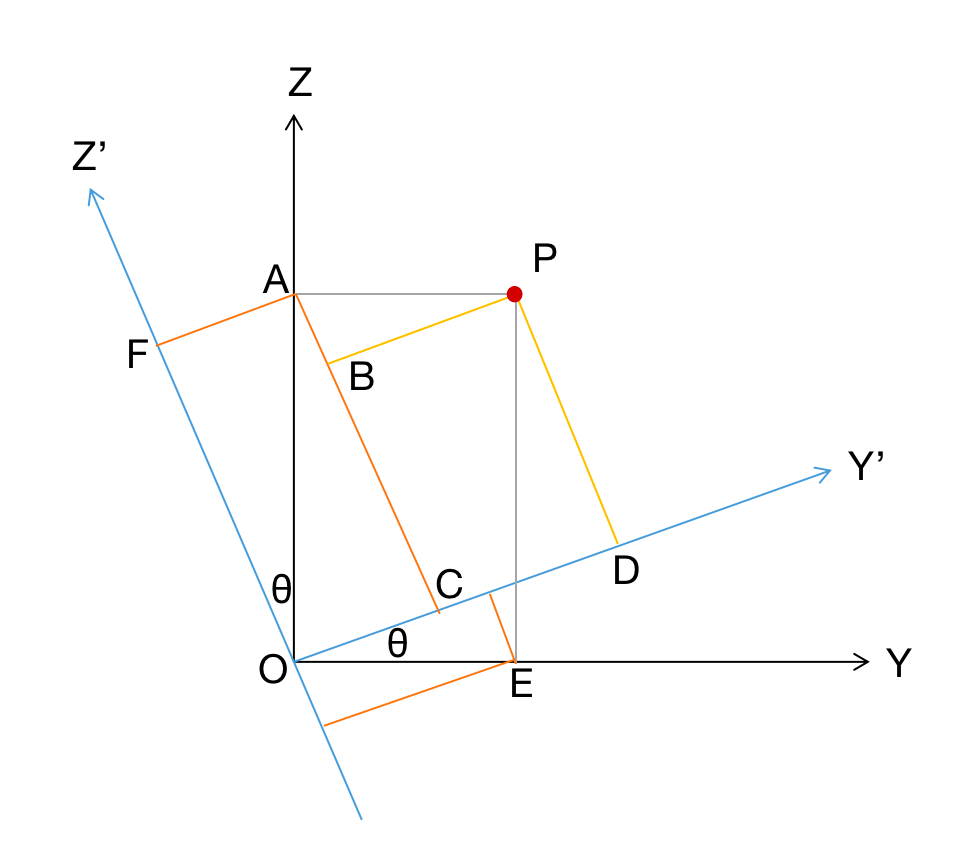
假设旋转角度为$\theta$,即$\angle{Y’OY}=\angle{Z’OZ}=\theta$。旋转前的坐标系为$X-Y-Z$,旋转后的坐标系为$X’-Y’-Z’$。假设点$P$在$X-Y-Z$中的坐标为$(X_w,Y_w,Z_w)$,旋转后,其在$X’-Y’-Z’$中的坐标为$(X_c,Y_c,Z_c)$:
\[X_c = X_w\] \[\begin{align} Y_c &= OC+CD \\&= OA \cdot \sin \theta + BP \\&= Z_w \sin \theta + AP \cdot \cos \theta \\&= Z_w \sin \theta + Y_w \cos \theta \end{align}\] \[\begin{align} Z_c &= PD \\&= AC - AB \\&= AO \cdot \cos \theta - AP \cdot \sin \theta \\&=Z_w \cos \theta - Y_w \sin \theta \end{align}\]写成矩阵相乘的形式:
\[\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} \tag{1}\]也可以写成:
\[\begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix} \tag{2}\]注意:这个例子用的是左手笛卡尔坐标系,同一旋转矩阵对应的旋转方向和右手笛卡尔坐标系相反。
其中旋转矩阵:
\[\mathbf{R} (X_A,\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \\ \end{bmatrix} \tag{3}\]或:
\[\mathbf{R} (X_A,\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \\ \end{bmatrix} \tag{4}\]依此类推,分别绕$Y$、$Z$轴的旋转矩阵为:
\[\mathbf{R} (Y_A , \theta) = \begin{bmatrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \\ \end{bmatrix}, \mathbf{R} (Y_A , \theta) = \begin{bmatrix} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \\ \end{bmatrix}\] \[\mathbf{R}(Z_A, \theta) = \begin{bmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}, \mathbf{R}(Z_A, \theta) = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]这里我们使用右手笛卡尔三维坐标系:
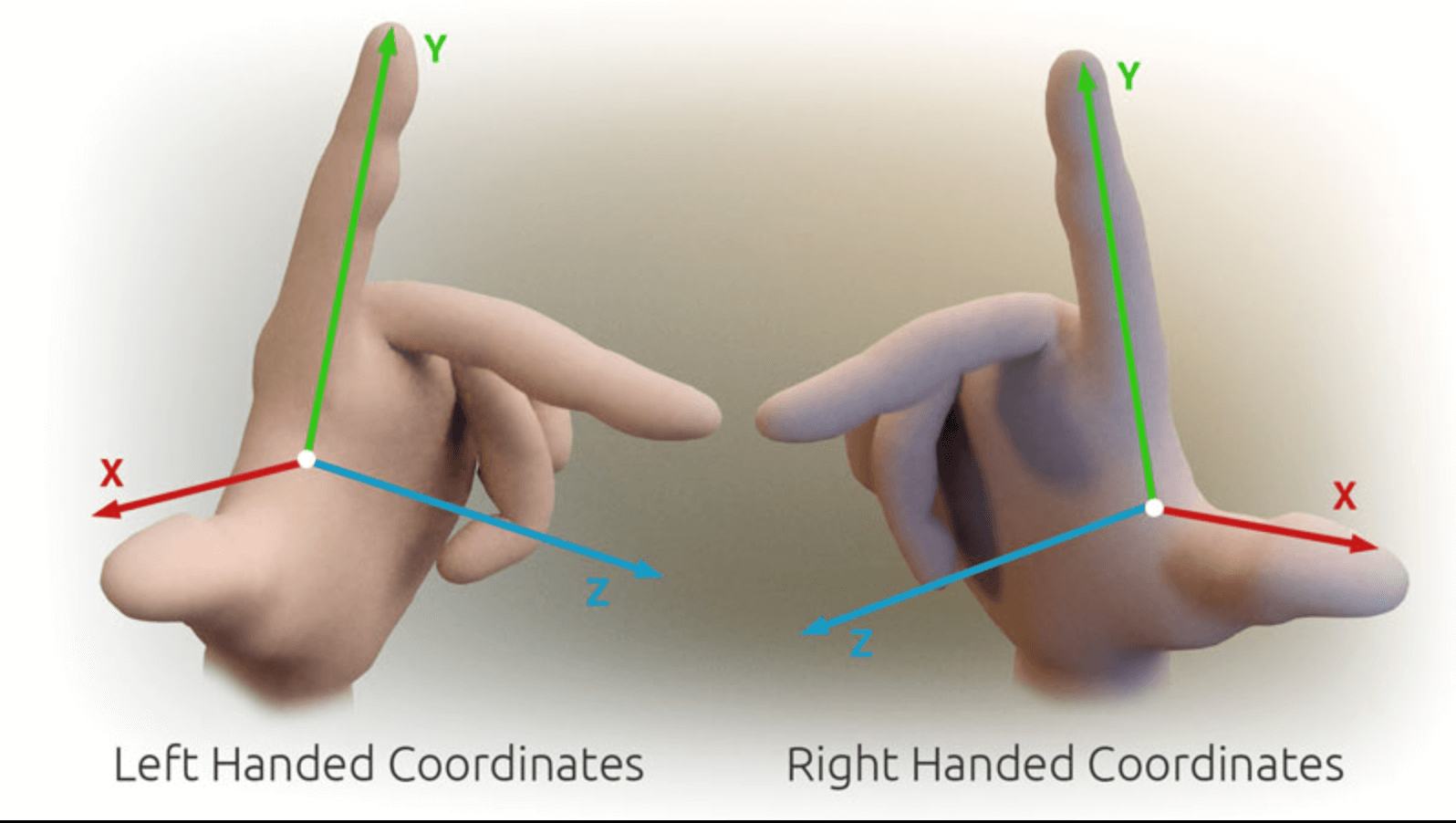
旋转可分为主动旋转与被动旋转。主动旋转是指将向量逆时针围绕旋转轴所做出的旋转。被动旋转是对坐标轴本身进行的逆时针旋转,它相当于主动旋转的逆操作。关于右手笛卡尔坐标系的$x-$,$y-$和$z-$轴的旋转分别叫做roll,pitch和yaw旋转:
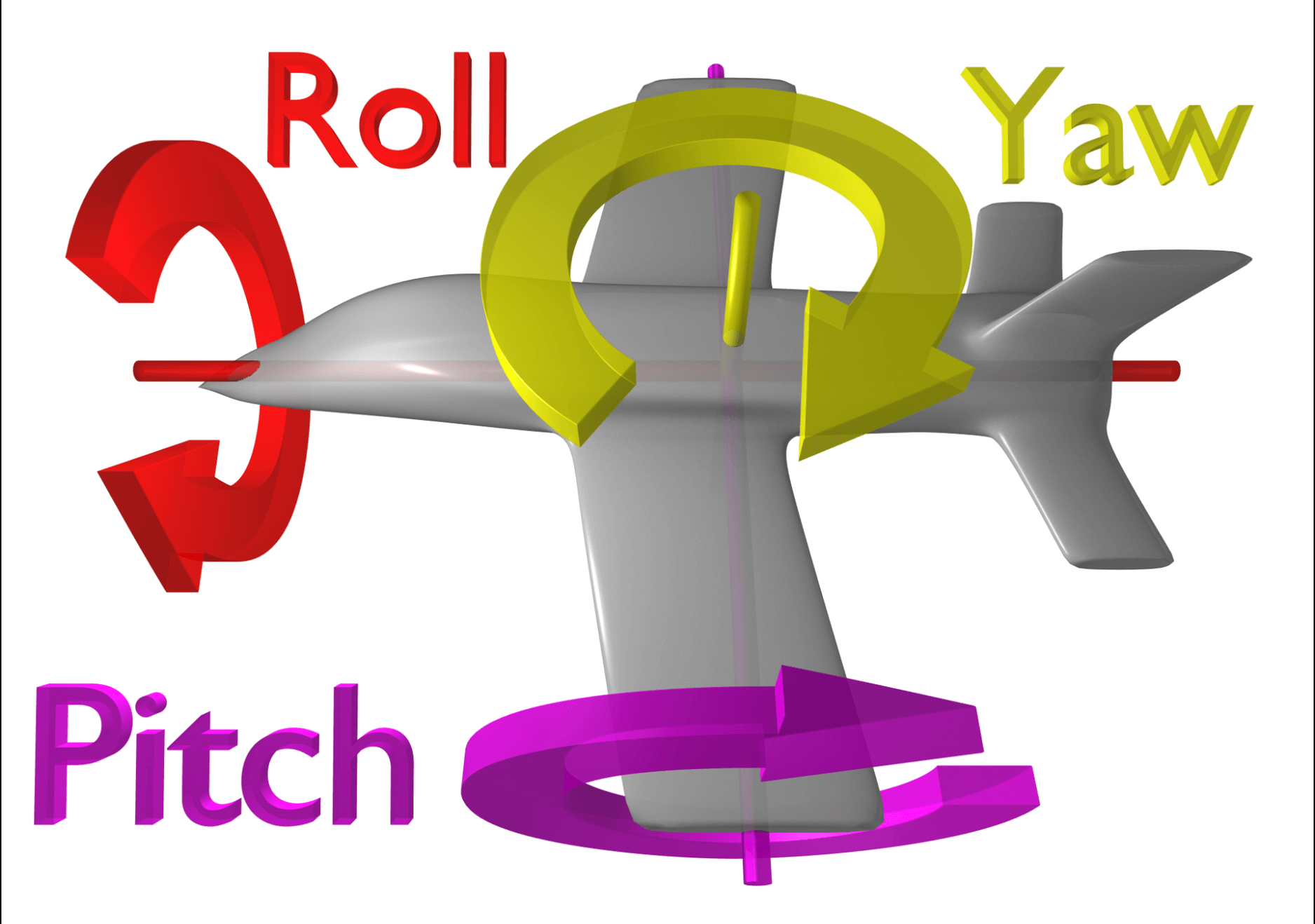
因为逆时针和顺时针旋转会得到不一样的旋转矩阵,所以我们统一如下:
👉绕$x-$轴的主动旋转定义为:
\[\mathbf{R} (X_A,\theta_x) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta_x & -\sin \theta_x \\ 0 & \sin \theta_x & \cos \theta_x \\ \end{bmatrix} = \exp \left( \theta_x \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{bmatrix} \right)\]这里的$\theta_x$是roll角,和右手螺旋的方向相同(在$yz$平面逆时针)。
👉绕$y-$轴的主动旋转定义为:
\[\mathbf{R} (Y_A , \theta_y) = \begin{bmatrix} \cos \theta_y & 0 & \sin \theta_y \\ 0 & 1 & 0 \\ -\sin \theta_y & 0 & \cos \theta_y \\ \end{bmatrix} = \exp \left( \theta_y \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \\ \end{bmatrix} \right)\]这里的$\theta_y$是pitch角,和右手螺旋的方向相同(在$zx$平面逆时针)。
👉绕$z-$轴的主动旋转定义为:
\[\mathbf{R}(Z_A, \theta_z) = \begin{bmatrix} \cos \theta_z & -\sin \theta_z & 0 \\ \sin \theta_z & \cos \theta_z & 0 \\ 0 & 0 & 1 \end{bmatrix} = \exp \left( \theta_z \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \right)\]这里的$\theta_z$是yaw角,和右手螺旋的方向相同(在$xy$平面逆时针)。
那么最终的旋转矩阵可表示为(设绕$X,Y,Z$轴旋转的角度分别为$\alpha,\beta,\gamma$):
\[\begin{align} \mathcal{M}(\alpha,\beta,\gamma) &= \mathcal{R}_z (\gamma) \mathcal{R}_y (\beta) \mathcal{R}_x (\alpha) \\&= \begin{bmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \\ \end{bmatrix} \\&= \begin{bmatrix} \cos \gamma \cos \beta & -\sin \gamma & \cos \gamma \sin \beta \\ \sin \gamma \cos \beta & \cos \gamma & \sin \gamma \sin \beta \\ -\sin \beta & 0 & \cos \beta \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \\ \end{bmatrix} \\&= \begin{bmatrix} \cos \gamma \cos \beta & -\sin \gamma \cos \alpha + \cos \gamma \sin \beta \sin \alpha & \sin \gamma \sin \alpha + \cos \gamma \sin \beta \cos \alpha \\ \sin \gamma \cos \beta & \cos \gamma \cos \alpha + \sin \gamma \sin \beta \sin \alpha & -\cos \gamma \sin \alpha + \sin \gamma \sin \beta \cos \alpha \\ -\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha \\ \end{bmatrix} \end{align}\]此时我们再加上平移向量$T$便可完整表示从世界坐标系到相机坐标系的这个刚体变换了:
\[\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \\ t_z \\ \end{bmatrix} = \mathbf{R} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} + \mathbf{T}\]可进一步写成如下形式:
\[\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \mathbf{R} & \mathbf{T} \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}\]其中,$\mathbf{R}$和$\mathbf{T}$便是相机的外参。
3.4.相机内参
👉首先考虑图像坐标系(xy)和像素坐标系(uv)之间的转换:
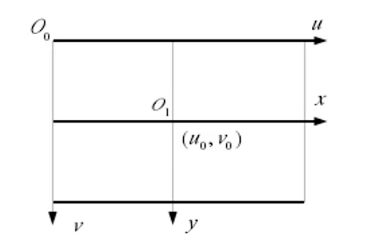
$dx$表示一个像素点在$x$方向的长度是多少毫米,$dy$表示一个像素点在$y$方向的长度是多少毫米。$(u_0,v_0)$为图像中心点。
👉然后考虑相机坐标系和图像坐标系之间的转换:
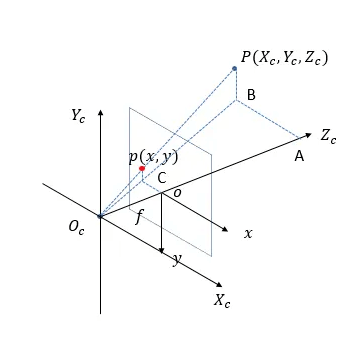
其中,$f$是焦距。结合第3.3部分的内容,我们最终可得到世界坐标系和像素坐标系之间的映射关系:
\[Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} =\begin{bmatrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \mathbf{R} & \mathbf{T} \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x & 0 & u_0 & 0 \\ 0 & f_y & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \mathbf{R} & \mathbf{T} \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix} \tag{5}\]其中,相机内参为:
\[\begin{bmatrix} f_x & 0 & u_0 & 0 \\ 0 & f_y & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix}\]相机外参为:
\[\begin{bmatrix} \mathbf{R} & \mathbf{T} \\ 0 & 1 \\ \end{bmatrix}\]式(5)也可写为:
\[s \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix} \tag{6}\]3.5.畸变参数
在几何光学和阴极射线管(CRT)显示中,畸变(distortion)是对直线投影的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了,这是一种光学畸变。畸变一般可以分为两大类,包括径向畸变(radial distortion)和切向畸变(tangential distortion)。畸变还有其他类型的畸变,但是没有径向畸变和切向畸变显著。
径向畸变来自于透镜形状,主要是由于透镜不同部位放大倍率不同造成的。切向畸变来自于整个相机的组装过程,主要是由于透镜安装与成像平面不平行造成的。
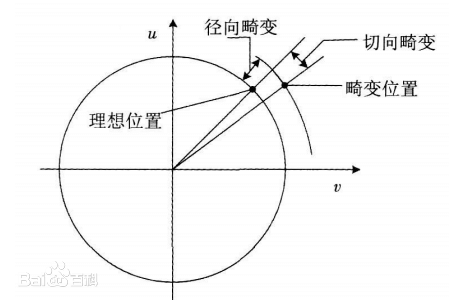
3.5.1.径向畸变
实际摄像机的透镜总是在成像仪的边缘产生显著的畸变,这种现象来源于“筒形”或“鱼眼”的影响。光线在远离透镜中心的地方比靠近中心的地方更加弯曲。对于常用的普通透镜来说,这种现象更加严重。对于径向畸变,成像仪中心(即光学中心)的畸变为0,随着向边缘移动,畸变越来越严重。径向畸变按照形状可分为三种:
- 桶形畸变(barrel distortion)
- 枕形畸变(pincushion distortion)
- 胡子畸变(mustache distortion)
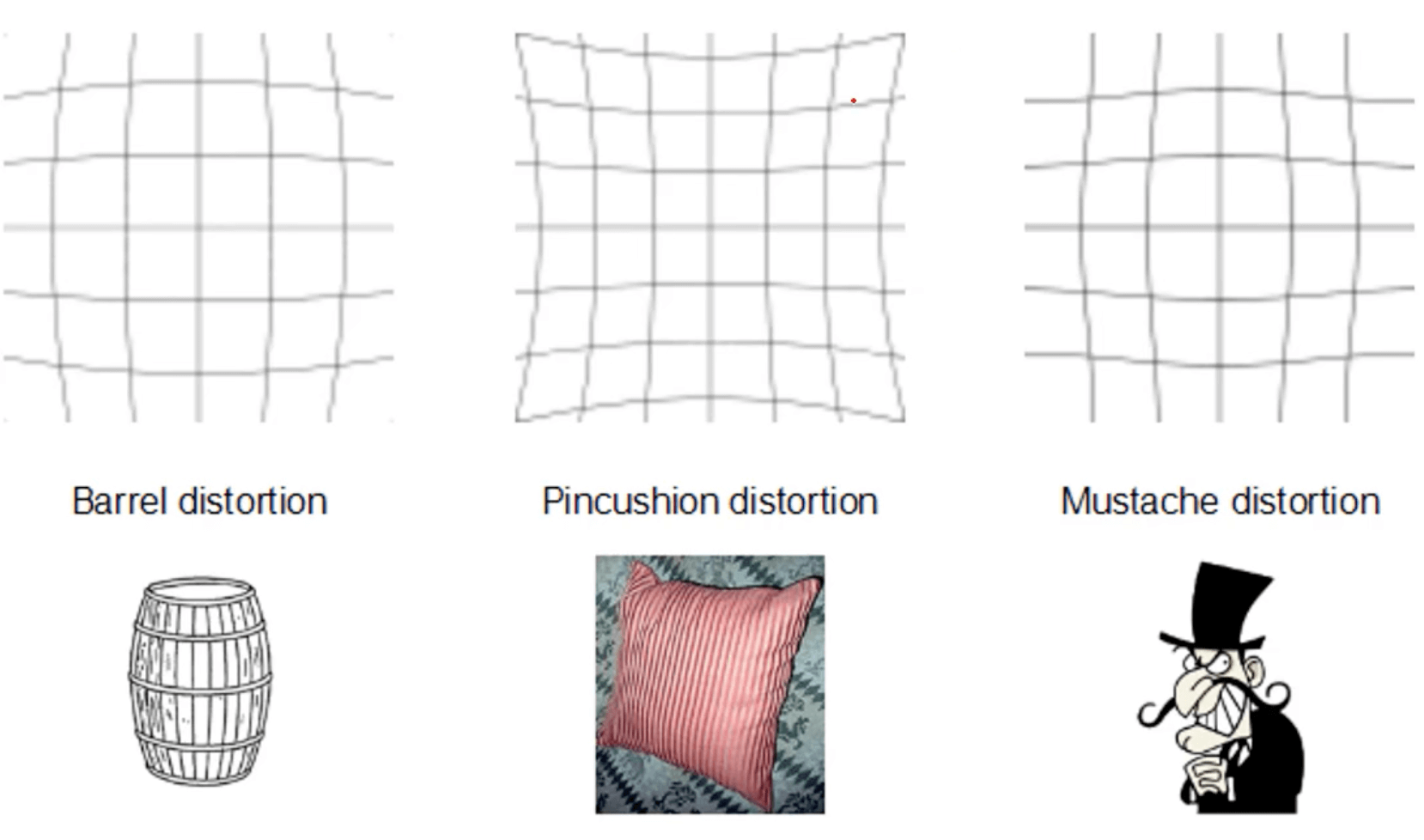
桶形畸变在便宜的网络摄像机中非常厉害,但在高端摄像机中不明显,因为这些透镜系统做了很多消除径向畸变的工作。
3.5.2.切向畸变
用两张图形象的解释下切向畸变:
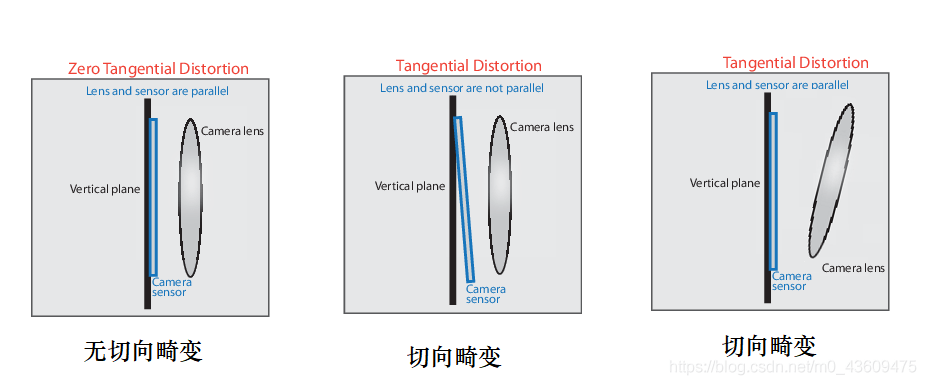
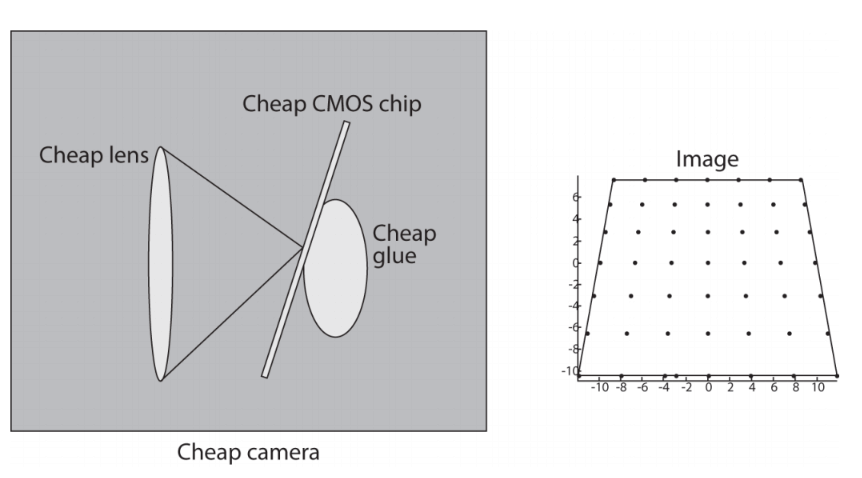
3.5.3.畸变校正
径向畸变校正公式:
\[x^{''} = x^{'} (1+k_1 r^2 + k_2 r^4 + k_3 r^6)\] \[y^{''} = y^{'} (1+k_1 r^2 + k_2 r^4 + k_3 r^6)\]切向畸变校正公式:
\[x^{''} = x^{'} +[ 2p_1 x^{'}y^{'} + p_2 (r^2+2x^{'2}) ]\] \[y^{''} = y^{'} +[ p_1 (r^2 + 2y^{'2}) + 2p_2 x^{'}y^{'}]\]结合式(5)或式(6),在考虑畸变的情况下,从世界坐标系到像素坐标系的映射过程可表示为(和OpenCV官方文档保持一致):
\[\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix} = \mathbf{R} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} + \mathbf{T}\] \[x^{'} = \frac{X_c}{Z_c}, y^{'} = \frac{Y_c}{Z_c}\] \[x^{''} = x^{'} \frac{1+k_1 r^2 + k_2 r^4 + k_3 r^6}{1+k_4 r^2 + k_5 r^4 + k_6 r^6} + 2p_1 x^{'}y^{'} + p_2 (r^2+2x^{'2}) + s_1 r^2 + s_2 r^4\] \[y^{''} = y^{'} \frac{1+k_1 r^2 + k_2 r^4 + k_3 r^6}{1+k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2y^{'2}) + 2p_2 x^{'}y^{'} + s_1 r^2 + s_2 r^4\] \[u = f_x * x^{''} + c_x\] \[v = f_y * y^{''} + c_y\]其中,$r^2 = x^{'2}+y^{'2}$,$k_1,k_2,k_3,k_4,k_5,k_6$表示径向畸变系数,$p_1,p_2$表示切向畸变系数,$s_1,s_2$表示薄棱镜畸变系数(thin prism distortion)。从上述映射过程中可以看出$(x^{'},y^{'},1)$(通过除以$Z_c$进行了归一化)是理想状态下无畸变的相机坐标系下的坐标,而$(x^{''},y^{''},1)$是在考虑畸变之后得到的实际的相机坐标系下的坐标。