本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.相机标定方法
相机标定方法有:传统相机标定法、主动视觉相机标定方法、相机自标定法、零失真相机标定法等。这些标定方法的目的就是求出相机的内参、外参和畸变系数。
本文即将要介绍的是张正友相机标定法。张正友相机标定法是张正友教授在1998年提出的基于单平面棋盘格的相机标定方法。该方法介于传统标定法和自标定法之间,但克服了传统标定法需要高精度三维标定物的缺点,而仅需使用一个打印出来的棋盘格就可以。同时相对于自标定法而言,提高了精度,便于操作。因此张氏标定法被广泛应用于计算机视觉方面。
2.倾斜因子
在相机标定时,我们通常假设倾斜因子(skew factor)为0以简化运算。但有时因为制作工艺的精度问题,倾斜因子可能并不是0,即感光板的横边和纵边并不垂直:
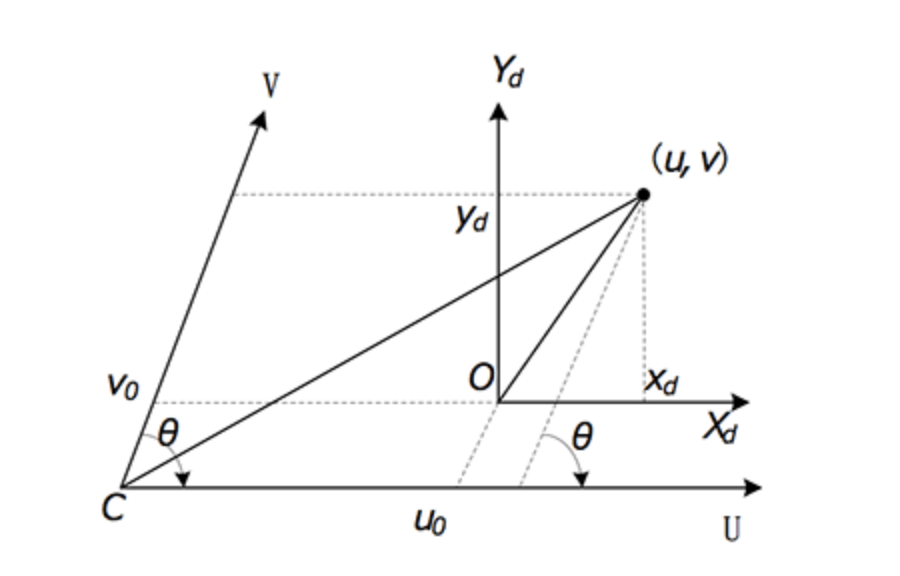
上图中,$O$是图像中心点,对应像素坐标系的$(u_0,v_0)$,$X_d - Y_d$为图像坐标系,$U-V$为像素坐标系,有:
\[u = u_0 + \frac{x_d}{dx} - \frac{y_d \cot \theta}{dx} \tag{1}\] \[v = v_0 + \frac{y_d}{dy \sin \theta} \tag{2}\]其中,$dx,dy$为像素在$x$和$y$方向上的物理尺寸。$cot$为余切函数,在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切:
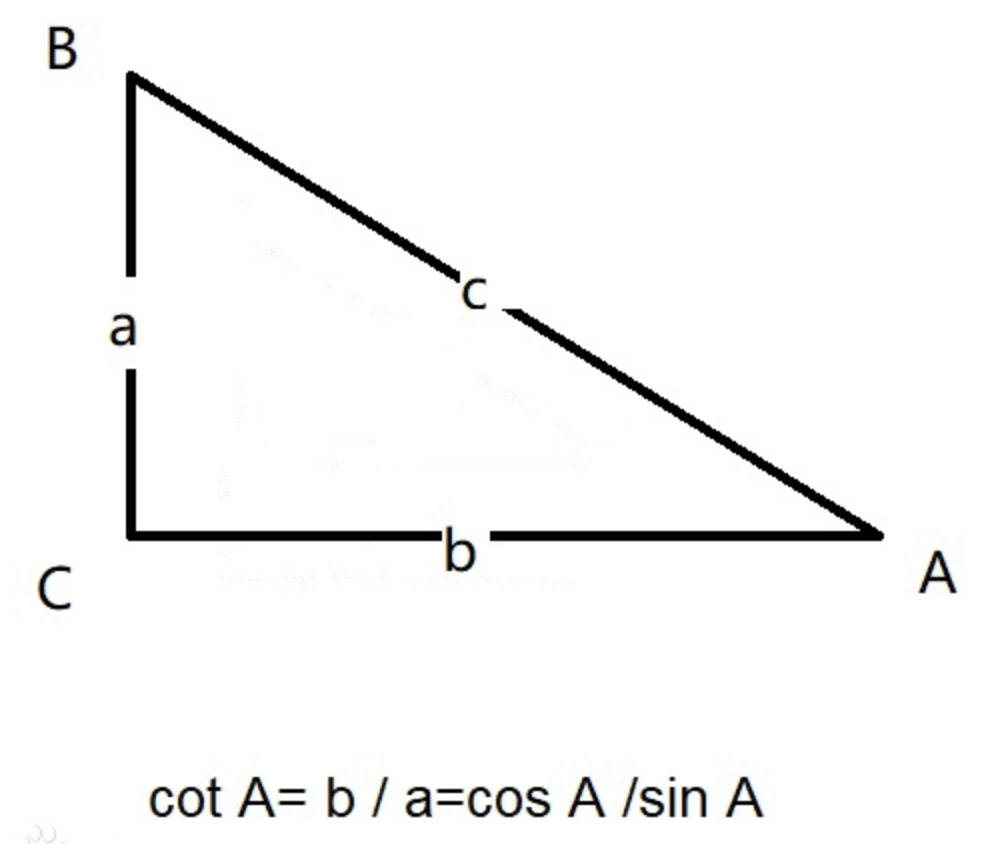
所以,在考虑倾斜因子的情况下,图像坐标系到像素坐标系的转换为:
\[\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{dx} & -\frac{\cot \theta}{dx} & u_0 \\ 0 & \frac{1}{dy \sin \theta} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x_d \\ y_d \\ 1 \end{bmatrix} \tag{3}\]此时相机的内参矩阵可表示为:
\[\begin{bmatrix} \frac{f}{dx} & -\frac{f \cot \theta}{dx} & u_0 \\ 0 & \frac{f}{dy \sin \theta} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} \alpha & \lambda & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \tag{4}\]3.张正友标定法
张正友标定法是基于棋盘格的相机标定方法,其将世界坐标系的$X-Y$平面放置在棋盘格标定板上,$Z$与标定板垂直,那么就相当于标定板上每个角点的$Z_w$都为0。因此,每个角点在世界坐标系和像素坐标系之间的映射关系可以表示为:
\[Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \alpha & \lambda & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \ \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 0 \\ 1 \\ \end{bmatrix} \tag{5}\]进一步化简为:
\[Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \alpha & \lambda & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & t_1 \\ r_{21} & r_{22} & t_2 \\ r_{31} & r_{32} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \\ \end{bmatrix} = \mathbf{A} \begin{bmatrix} \mathbf{r}_1 & \mathbf{r}_2 & \mathbf{t} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \\ \end{bmatrix} \tag{6}\]张正友标定法的思路如下:
- 求解内参矩阵和外参矩阵的积。
- 求解内参矩阵。
- 求解外参矩阵。
3.1.求解内参矩阵和外参矩阵的积
定义单应性(homography)矩阵$\mathbf{H}$:
\[\mathbf{H} = \mathbf{A} \begin{bmatrix} \mathbf{r}_1 & \mathbf{r}_2 & \mathbf{t} \\ \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} \tag{7}\]则世界坐标系和像素坐标系之间的映射关系可表示为:
\[\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \frac{1}{Z_c} \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \\ \end{bmatrix} \tag{8}\]由上式可知:
\[u = (h_{11}X_w + h_{12}Y_w + h_{13}) \frac{1}{Z_c} \tag{9}\] \[v = (h_{21}X_w + h_{22}Y_w + h_{23}) \frac{1}{Z_c} \tag{10}\] \[1 = (h_{31}X_w + h_{32}Y_w + h_{33}) \frac{1}{Z_c} \tag{11}\]因此我们可以消掉尺度因子$Z_c$:
\[u = \frac{h_{11}X_w + h_{12}Y_w + h_{13}}{h_{31}X_w + h_{32}Y_w + h_{33}} \tag{12}\] \[v = \frac{h_{21}X_w + h_{22}Y_w + h_{23}}{h_{31}X_w + h_{32}Y_w + h_{33}} \tag{13}\]这里使用的是齐次坐标系,也就是说可以进行任意尺度的缩放且不改变等式结果:
\[u = \frac{h_{11}X_w + h_{12}Y_w + h_{13}}{h_{31}X_w + h_{32}Y_w + h_{33}} = \frac{kh_{11}X_w + kh_{12}Y_w + kh_{13}}{kh_{31}X_w + kh_{32}Y_w +k h_{33}} \tag{14}\] \[v = \frac{h_{21}X_w + h_{22}Y_w + h_{23}}{h_{31}X_w + h_{32}Y_w + h_{33}} = \frac{kh_{21}X_w + kh_{22}Y_w + kh_{23}}{kh_{31}X_w + kh_{32}Y_w + kh_{33}} \tag{15}\]此时我们便需要一个约束条件来使得$\mathbf{H}$是唯一的,这个约束条件可以是:
\[h_{33} = 1 \tag{16}\]或:
\[h_{11}^2 + h_{12}^2 + h_{13}^2 + h_{21}^2 + h_{22}^2 + h_{23}^2 + h_{31}^2 + h_{32}^2 + h_{33}^2=1 \tag{17}\]我们可以将式(12)和式(13)写成如下形式:
\[h_{11}X_w + h_{12}Y_w + h_{13} - h_{31}X_w u - h_{32}Y_w u - h_{33} u =0 \tag{18}\] \[h_{21}X_w + h_{22}Y_w + h_{23} - h_{31}X_w v - h_{32}Y_w v - h_{33} v = 0 \tag{19}\]写成矩阵相乘的形式:
\[\begin{bmatrix} X_w & Y_w & 1 & 0 & 0 & 0 & -X_wu & -Y_wu & -u \\ 0 & 0 & 0 & X_w & Y_w & 1 & -X_wv & -Y_wv & -v \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \end{bmatrix} \begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ \end{bmatrix} \tag{20}\]$\mathbf{H}$的自由度为8,因此理论上我们只需要4个点对(8个方程)即可求出$\mathbf{H}$。但是这些都只是理论推导,在真实的应用场景中,我们计算的点对中都会包含噪声。比如点的位置偏差几个像素,甚至出现特征点对误匹配的现象,如果只使用4个点对来计算单应性矩阵$\mathbf{H}$,那会出现很大的误差。因此,为了使得计算更精确,一般都会使用远大于4个点对来计算单应性矩阵$\mathbf{H}$,此时,我们便可以使用Levenberg-Marquarat(LM)等优化算法来求得矩阵$\mathbf{H}$。
3.2.求解内参矩阵
已知矩阵$\mathbf{H}$后,接下来我们先来求内参矩阵$\mathbf{A}$。其中,$\mathbf{r}_1,\mathbf{r}_2$作为旋转矩阵$\mathbf{R}$的两列,存在单位正交的关系,即:
\[\begin{align} \mathbf{r}_1^T \mathbf{r}_2 &= \cos \gamma \cos \beta \cdot (-\sin \gamma \cos \alpha + \cos \gamma \sin \beta \sin \alpha) + \sin \gamma \cos \beta \cdot (\cos \gamma \cos \alpha + \sin \gamma \sin \beta \sin \alpha) - \sin \beta \cos \beta \sin \alpha \\&= -\cos \gamma \cos \beta \sin \gamma \cos \alpha + \cos \gamma \cos \beta \cos \gamma \sin \beta \sin \alpha + \sin \gamma \cos \beta \cos \gamma \cos \alpha + \sin \gamma \cos \beta \sin \gamma \sin \beta \sin \alpha - \sin \beta \cos \beta \sin \alpha \\&= \cos \beta \sin \beta \sin \alpha (\cos^2 \gamma + \sin^2 \gamma) - \sin \beta \cos \beta \sin \alpha \\&= 0 \end{align} \tag{21}\] \[\begin{align} \mathbf{r}_1^T \mathbf{r}_1 &= \cos^2 \gamma \cos^2 \beta + \sin^2 \gamma \cos^2 \beta + \sin^2 \beta \\&= 1 \end{align} \tag{22}\] \[\begin{align} \mathbf{r}_2^T \mathbf{r}_2 &= \sin^2 \gamma \cos^2 \alpha \\& \quad -2\sin \gamma \cos \alpha \cos \gamma \sin \beta \sin \alpha \\& \quad + \cos^2 \gamma \sin^2 \beta \sin^2 \alpha \\& \quad + \cos^2 \gamma \cos^2 \alpha \\& \quad + 2\cos \gamma \cos \alpha \sin \gamma \sin \beta \sin \alpha \\& \quad + \sin^2 \gamma \sin^2 \beta \sin^2 \alpha \\& \quad + \cos^2 \beta \sin^2 \alpha \\&=1 \\ \end{align} \tag{23}\]旋转矩阵见:相机外参。
我们将矩阵$\mathbf{H}$表示为:
\[\mathbf{H} = \begin{bmatrix} \mathbf{h}_1 & \mathbf{h}_2 & \mathbf{h}_3 \\ \end{bmatrix} \tag{24}\]则由$\mathbf{H}$和$\mathbf{r}_1,\mathbf{r}_2$的关系,可知:
\[\mathbf{r}_1 = \mathbf{A}^{-1} \mathbf{h}_1 \tag{25}\] \[\mathbf{r}_2 = \mathbf{A}^{-1} \mathbf{h}_2 \tag{26}\]将式(25),式(26)带入式(21)~(23):
\[\mathbf{h}_1^T \mathbf{A}^{-T} \mathbf{A}^{-1} \mathbf{h}_2 = 0 \tag{27}\] \[\mathbf{h}_1^T \mathbf{A}^{-T} \mathbf{A}^{-1} \mathbf{h}_1 = \mathbf{h}_2^T \mathbf{A}^{-T} \mathbf{A}^{-1} \mathbf{h}_2 = 1 \tag{28}\]式(27)和式(28)中均存在$\mathbf{A}^{-T} \mathbf{A}^{-1}$。因此我们记$\mathbf{A}^{-T} \mathbf{A}^{-1} = \mathbf{B}$,我们先解出$\mathbf{B}$,再通过矩阵$\mathbf{B}$来求解内参矩阵$\mathbf{A}$。我们知道矩阵$\mathbf{A}$为:
\[\mathbf{A} = \begin{bmatrix} \alpha & \gamma & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \tag{29}\]可求得:
\[\mathbf{A}^{-1} = \begin{bmatrix} \frac{1}{\alpha} & -\frac{\lambda}{\alpha \beta} & \frac{\gamma v_0 - \beta u_0}{\alpha \beta} \\ 0 & \frac{1}{\beta} & -\frac{v_0}{\beta} \\ 0 & 0 & 1 \\ \end{bmatrix} \tag{30}\]则可计算矩阵$\mathbf{B}$为:
\[\begin{align} \mathbf{B} &= \mathbf{A}^{-T} \mathbf{A}^{-1} \equiv \begin{bmatrix} B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22} & B_{23} \\ B_{13} & B_{23} & B_{33} \\ \end{bmatrix} \\&= \begin{bmatrix} \frac{1}{\alpha^2} & -\frac{\gamma}{\alpha^2 \beta} & \frac{v_0 \gamma - u_0 \beta}{\alpha^2 \beta} \\ -\frac{\gamma}{\alpha^2 \beta} & \frac{\gamma^2}{\alpha^2 \beta^2} + \frac{1}{\beta^2} & -\frac{\gamma (v_0 \gamma - u_0 \beta)}{\alpha^2 \beta^2}-\frac{v_0}{\beta^2} \\ \frac{v_0 \gamma - u_0 \beta}{\alpha^2 \beta} & -\frac{\gamma (v_0 \gamma - u_0 \beta)}{\alpha^2 \beta^2} - \frac{v_0}{\beta^2} & \frac{(v_0 \gamma - u_0 \beta)^2}{\alpha^2 \beta^2} + \frac{v_0^2}{\beta^2} + 1 \\ \end{bmatrix} \end{align} \tag{31}\]可以看出,矩阵$\mathbf{B}$是一个对称矩阵。我们将矩阵$\mathbf{B}$带回到式(27),(28):
\[\mathbf{h}_1^T \mathbf{B} \mathbf{h}_2 = 0 \tag{32}\] \[\mathbf{h}_1^T \mathbf{B} \mathbf{h}_1 = \mathbf{h}_2^T \mathbf{B} \mathbf{h}_2 = 1 \tag{33}\]因此为了求解矩阵$\mathbf{B}$,我们必须计算$\mathbf{h}_i^T \mathbf{B} \mathbf{h}_j$:
\[\begin{align} \mathbf{h}_i^T \mathbf{B} \mathbf{h}_j &= \begin{bmatrix} h_{1i} & h_{2i} & h_{3i} \end{bmatrix} \begin{bmatrix} B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22} & B_{23} \\ B_{13} & B_{23} & B_{33} \\ \end{bmatrix} \begin{bmatrix} h_{1j} \\ h_{2j} \\ h_{3j} \\ \end{bmatrix} \\&= \begin{bmatrix} h_{1i}h_{1j} & h_{1i}h_{2j}+h_{2i}h_{1j} & h_{2i}h_{2j} & h_{1i}h_{3j}+h_{3i}h_{1j} & h_{2i}h_{3j}+h_{3i}h_{2j} & h_{3i}h_{3j} \\ \end{bmatrix} \begin{bmatrix} B_{11} \\ B_{12} \\ B_{22} \\ B_{13} \\ B_{23} \\ B_{33} \\ \end{bmatrix} \\&= \mathbf{v}_{ij}^T \mathbf{b} \end{align} \tag{34}\]由式(32)~(34)可得:
\[\mathbf{v}_{12}^T \mathbf{b} = 0 \tag{35}\] \[\mathbf{v}_{11}^T \mathbf{b} = \mathbf{v}_{22}^T \mathbf{b} = 1 \tag{36}\]即:
\[\begin{bmatrix} \mathbf{v}_{12}^T \\ \mathbf{v}_{11}^T-\mathbf{v}_{22}^T \\ \end{bmatrix} \mathbf{b} = \mathbf{V} \mathbf{b} = 0 \tag{37}\]由于矩阵$\mathbf{H}$已经算出来了,所以$\mathbf{V}$是已知的。每张标定板图像可以提供一个$\mathbf{V} \mathbf{b} = 0$的约束关系,该约束关系含有两个约束方程。但是$\mathbf{b}$有6个未知元素。因此,单张图像提供的两个约束方程是不足以解出$\mathbf{b}$的。因此,我们只要取3张标定板图像,得到3个$\mathbf{V} \mathbf{b} = 0$的约束关系,即6个方程,即可求得$\mathbf{b}$。当标定板图像的个数大于3时(事实上一般需要15到20张标定板图像),可采用最小二乘拟合最佳的向量$\mathbf{b}$,从而得到矩阵$\mathbf{B}$。矩阵$\mathbf{B}$和相机内参的对应关系见下:
\[v_0 = \frac{B_{12}B_{13}-B_{11}B_{23}}{B_{11}B_{22}-B_{12}^2} \tag{38}\] \[\alpha = \sqrt{\frac{1}{B_{11}}} \tag{39}\] \[\beta = \sqrt{\frac{B_{11}}{B_{11}B_{22}-B_{12}^2}} \tag{40}\] \[\gamma = -B_{12}\alpha^2 \beta \tag{41}\] \[u_0 = \frac{\gamma v_0}{\beta} - B_{13} \alpha^2 \tag{42}\]3.3.求解外参矩阵
对于同一个相机来说,内参矩阵是不变的,而每个标定板图像都会对应一个外参矩阵。外参矩阵的计算如下:
\[\mathbf{r}_1 = \mathbf{A}^{-1} \mathbf{h}_1 \tag{43}\] \[\mathbf{r}_2 = \mathbf{A}^{-1} \mathbf{h}_2 \tag{44}\] \[\mathbf{r}_3 = \mathbf{r}_1 \times \mathbf{r}_2 \tag{45}\] \[\mathbf{t} = \mathbf{A}^{-1} \mathbf{h}_3 \tag{46}\]3.4.求解畸变系数
张正友标定法仅仅考虑了畸变模型中影响较大的径向畸变。本部分的符号定义沿用此处,不再重复解释。
\[x^{''} = x^{'} (1+k_1 r^2 + k_2 r^4) \tag{47}\] \[y^{''} = y^{'} (1+k_1 r^2 + k_2 r^4) \tag{48}\] \[u^{''} = f_x * x^{''} + c_x\quad , \quad v^{''} = f_y * y^{''} + c_y \tag{49}\] \[u^{'} = f_x * x^{'} + c_x\quad , \quad v^{'} = f_y * y^{'} + c_y \tag{50}\]其中,$u^{'},v^{'}$为理想状态下无畸变的像素坐标,$u^{''},v^{''}$为考虑畸变之后实际的像素坐标。由式(47)~(50)可得:
\[u^{''}-c_x = (u^{'}-c_x)(1+k_1 r^2 + k_2 r^4) \tag{51}\] \[v^{''}-c_y = (v^{'}-c_y)(1+k_1 r^2 + k_2 r^4) \tag{52}\]化简可得:
\[u^{''}=u^{'}+(u^{'}-c_x)(k_1 r^2 + k_2 r^4) \tag{53}\] \[v^{''}=v^{'}+(v^{'}-c_y)(k_1 r^2 + k_2 r^4) \tag{54}\]合在一起可表示为:
\[\begin{bmatrix} (u^{'}-c_x)r^2 & (u^{'}-c_x)r^4 \\ (v^{'}-c_y)r^2 & (v^{'}-c_y)r^4 \\ \end{bmatrix} \begin{bmatrix} k_1 \\ k_2 \\ \end{bmatrix} = \begin{bmatrix} u^{''} - u^{'} \\ v^{''}-v^{'} \\ \end{bmatrix} \tag{55}\]式(55)中只有$k_1,k_2$是未知的。每一个角点都可以构造上述两个等式,如果有多张图像,每幅图像都有若干个角点,则可将得到的所有等式组合起来,最后通过最小二乘法求得$k_1,k_2$。扩展到2阶以上的情况是类似的,在此不再赘述。