【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.流形学习
流形学习(manifold learning)是一类借鉴了拓扑流形概念的降维方法。“流形”是在局部与欧氏空间同胚的空间,换言之,它在局部具有欧氏空间的性质,能用欧氏距离来进行距离计算。这给降维方法带来了很大的启发:若低维流形嵌入到高维空间中,则数据样本在高维空间的分布虽然看上去非常复杂,但在局部上仍具有欧氏空间的性质,因此,可以容易地在局部建立降维映射关系,然后再设法将局部映射关系推广到全局。当维数被降至二维或三维时,能对数据进行可视化展示,因此流形学习也可被用于可视化。本节介绍两种著名的流形学习方法。
2.等度量映射
等度量映射(Isometric Mapping,简称Isomap)的基本出发点,是认为低维流形嵌入到高维空间之后,直接在高维空间中计算直线距离具有误导性,因为高维空间中的直线距离在低维嵌入流形上是不可达的。如图10.7(a)所示,低维嵌入流形上两点间的距离是“测地线”(geodesic)距离:想象一只虫子从一点爬到另一点,如果它不能脱离曲面行走,那么图10.7(a)中的红色曲线是距离最短的路径,即S曲面上的测地线,测地线距离是两点之间的本真距离。显然,直接在高维空间中计算直线距离是不恰当的。
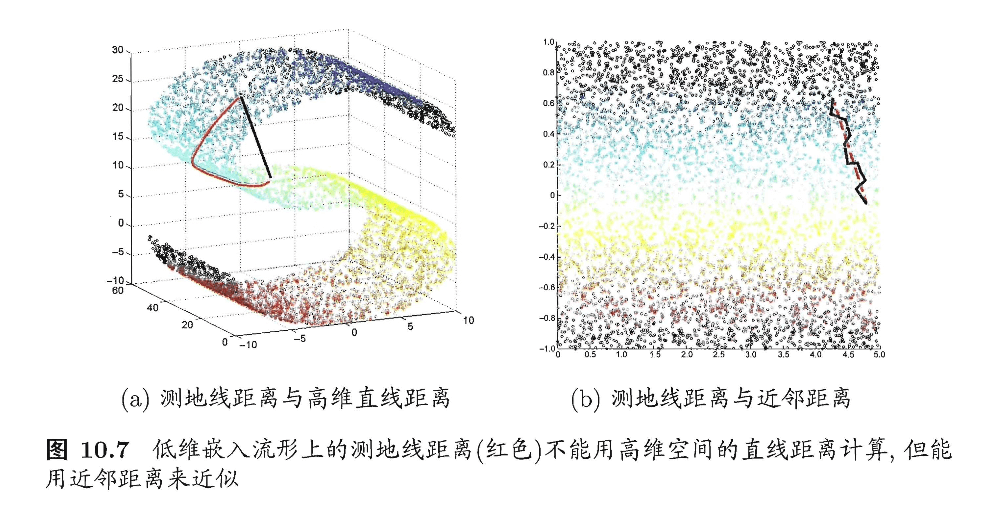
那么,如何计算测地线距离呢?这时我们可利用流形在局部上与欧氏空间同胚这个性质,对每个点基于欧氏距离找出其近邻点,然后就能建立一个近邻连接图,图中近邻点之间存在连接,而非近邻点之间不存在连接,于是,计算两点之间测地线距离的问题,就转变为计算近邻连接图上两点之间的最短路径问题。从图10.7(b)可看出,基于近邻距离逼近能获得低维流形上测地线距离很好的近似。
在近邻连接图上计算两点间的最短路径,可采用著名的Dijkstra算法或Floyd算法,在得到任意两点的距离之后,就可通过MDS方法来获得样本点在低维空间中的坐标。图10.8给出了Isomap算法描述。

需注意的是,Isomap仅是得到了训练样本在低维空间的坐标,对于新样本,如何将其映射到低维空间呢?这个问题的常用解决方案,是将训练样本的高维空间坐标作为输入、低维空间坐标作为输出,训练一个回归学习器来对新样本的低维空间坐标进行预测。这显然仅是一个权宜之计,但目前似乎并没有更好的办法。
对近邻图的构建通常有两种做法,一种是指定近邻点个数,例如欧氏距离最近的$k$个点为近邻点,这样得到的近邻图称为$k$近邻图;另一种是指定距离阈值$\epsilon$,距离小于$\epsilon$的点被认为是近邻点,这样得到的近邻图称为$\epsilon$近邻图。两种方式均有不足,例如若近邻范围指定得较大,则距离很远的点可能被误认为近邻,这样就出现“短路”问题;近邻范围指定得较小,则图中有些区域可能与其他区域不存在连接,这样就出现“断路”问题,短路与断路都会给后续的最短路径计算造成误导。
3.局部线性嵌入
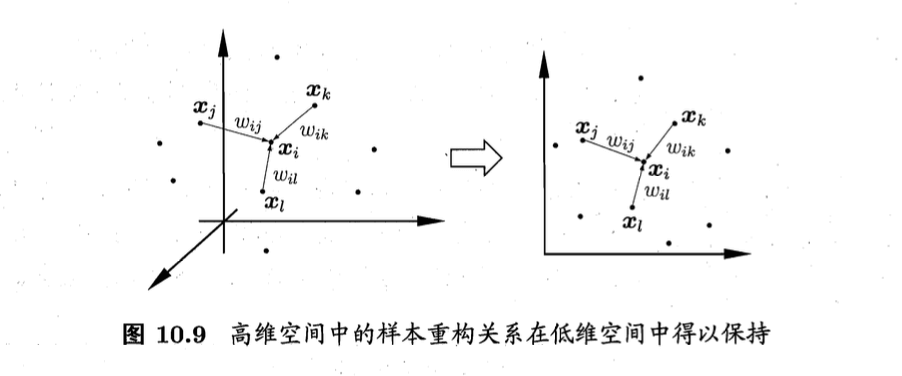
与Isomap试图保持近邻样本之间的距离不同,局部线性嵌入(Locally Linear Embedding,简称LLE)试图保持邻域内样本之间的线性关系。如图10.9所示,假定样本点$\mathbf{x}_i$的坐标能通过它的邻域样本$\mathbf{x}_j,\mathbf{x}_k,\mathbf{x}_l$的坐标通过线性组合而重构出来,即
\[\mathbf{x}_i=w_{ij}\mathbf{x}_j+w_{ik}\mathbf{x}_k+w_{il}\mathbf{x}_l \tag{10.26}\]LLE希望式(10.26)的关系在低维空间中得以保持。
LLE先为每个样本$\mathbf{x}_i$找到其近邻下标集合$Q_i$,然后计算出基于$Q_i$中的样本点对$\mathbf{x}_i$进行线性重构的系数$\mathbf{w}_i$:
\[\begin{align*} &\min \limits_{\mathbf{w}_1,\mathbf{w}_2,...,\mathbf{w}_m} \sum^m_{i=1} \left|\left| \mathbf{x}_i - \sum_{j\in Q_i} w_{ij} \mathbf{x}_j \right|\right| _2 ^2 \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} \quad \quad s.t.& \sum_{j\in Q_i} w_{ij}=1 \\ \end{array} \end{align*} \tag{10.27}\]其中$\mathbf{x}_i$和$\mathbf{x}_j$均为已知,令$C_{jk}=(\mathbf{x}_i-\mathbf{x}_j)^T(\mathbf{x}_i-\mathbf{x}_k)$,$w_{ij}$有闭式解:
\[w_{ij}=\frac{\sum_{k \in Q_i} C_{jk}^{-1}}{\sum_{l,s\in Q_i} C_{ls}^{-1}} \tag{10.28}\]LLE在低维空间中保持$\mathbf{w}_i$不变,于是$\mathbf{x}_i$对应的低维空间坐标$\mathbf{z}_i$可通过下式求解:
\[\min \limits_{\mathbf{z}_1,\mathbf{z}_2,...,\mathbf{z}_m} \sum^m_{i=1} \left|\left| \mathbf{z}_i - \sum_{j\in Q_i} w_{ij} \mathbf{z}_j \right|\right| _2 ^2 \tag{10.29}\]式(10.27)与(10.29)的优化目标同形,唯一的区别是式(10.27)中需确定的是$\mathbf{w}_i$,而式(10.29)中需确定的是$\mathbf{x}_i$对应的低维空间坐标$\mathbf{z}_i$。
令$\mathbf{Z}=(\mathbf{z}_1,\mathbf{z}_2,…,\mathbf{z}_m)\in \mathbb{R}^{d’ \times m}$,$(\mathbf{W})_{ij}=w_{ij}$,
\[\mathbf{M}=(\mathbf{I}-\mathbf{W})^T(\mathbf{I}-\mathbf{W}) \tag{10.30}\]则式(10.29)可重写为
\[\begin{align*} &\min \limits_{\mathbf{Z}} \text{tr}(\mathbf{ZMZ^T}) \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& \mathbf{ZZ}^T=\mathbf{I} \\ \end{array} \end{align*} \tag{10.31}\]式(10.31)可通过特征值分解求解:$\mathbf{M}$最小的$d’$个特征值对应的特征向量组成的矩阵即为$\mathbf{Z}^T$。
此处和后续推导不太一样,详见第3.2部分。
LLE的算法描述如图10.10所示。算法第4行显示出:对于不在样本$\mathbf{x}_i$邻域区域的样本$\mathbf{x}_j$,无论其如何变化都对$\mathbf{x}_i$和$\mathbf{z}_i$没有任何影响;这种将变动限制在局部的思想在许多地方都有用。

3.1.式(10.28)的推导
若令
\[\mathbf{x}_i \in \mathbb{R}^{d \times 1}\] \[Q_i=\{q_i^1, q_i^2,...,q_i^n \}\]则式(10.27)的目标函数可以进行如下恒等变形:
\[\begin{align} \sum^m_{i=1} \left|\left| \mathbf{x}_i - \sum_{j\in Q_i} w_{ij} \mathbf{x}_j \right|\right| _2 ^2 &= \sum^m_{i=1} \left|\left| \sum_{j\in Q_i} w_{ij} \mathbf{x}_i - \sum_{j\in Q_i} w_{ij} \mathbf{x}_j \right|\right| _2 ^2 \\&= \sum^m_{i=1} \left|\left| \sum_{j\in Q_i} w_{ij} (\mathbf{x}_i - \mathbf{x}_j )\right|\right| _2 ^2 \\&= \sum^m_{i=1} \parallel \mathbf{X}_i \mathbf{w}_i \parallel _2^2 \\&= \sum_{i=1}^m \mathbf{w}_i^T \mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i \end{align}\]其中,
\[\mathbf{w}_i = \begin{bmatrix} w_{iq_i^1} \\ w_{iq_i^2} \\ \vdots \\ w_{iq_i^n} \end{bmatrix} \in \mathbb{R}^{n\times 1}\] \[\mathbf{X}_i = \begin{bmatrix} \mathbf{x}_i - \mathbf{x}_{q_i^1} & \mathbf{x}_i - \mathbf{x}_{q_i^2} & \cdots & \mathbf{x}_i - \mathbf{x}_{q_i^n} \\ \end{bmatrix} \in \mathbb{R}^{d\times n}\]同理,式(10.27)的约束条件也可以进行如下恒等变形:
\[\sum_{j\in Q_i} w_{ij}=\mathbf{w}_i^T \mathbf{I} = 1\]其中,
\[\mathbf{I} = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \\ \end{bmatrix} \in \mathbb{R}^{n\times 1}\]所以,式(10.27)可以重写为:
\[\begin{align*} &\min \limits_{\mathbf{w}_1,\mathbf{w}_2,...,\mathbf{w}_m} \sum^m_{i=1} \mathbf{w}_i^T \mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} \quad \quad s.t.& \mathbf{w}_i^T \mathbf{I} = 1 \\ \end{array} \end{align*}\]显然,此问题为带约束的优化问题,因此可以考虑使用拉格朗日乘子法来进行求解。由拉格朗日乘子法可得此优化问题的拉格朗日函数为:
\[L(\mathbf{w}_1,\mathbf{w}_2,...,\mathbf{w}_m,\lambda)=\sum_{i=1}^m \mathbf{w}_i^T \mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i + \lambda (\mathbf{w}_i^T \mathbf{I} - 1)\]对拉格朗日函数关于$\mathbf{w}_i$求偏导并令其等于0可得:
\[\begin{align} \frac{\partial L(\mathbf{w}_1,\mathbf{w}_2,...,\mathbf{w}_m,\lambda)}{\partial \mathbf{w}_i} &= \frac{\partial [ \sum_{i=1}^m \mathbf{w}_i^T \mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i + \lambda (\mathbf{w}_i^T \mathbf{I} - 1) ]}{ \partial \mathbf{w}_i} \\&=\frac{\partial [ \mathbf{w}_i^T \mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i + \lambda (\mathbf{w}_i^T \mathbf{I} - 1) ]}{ \partial \mathbf{w}_i} \\&= 0 \end{align}\]又由矩阵微分公式
\[\frac{\partial \mathbf{x}^T \mathbf{Bx}}{\partial \mathbf{x}}=(\mathbf{B}+\mathbf{B}^T)\mathbf{x}\] \[\frac{\partial \mathbf{x}^T \mathbf{a}}{\partial \mathbf{x}}=\mathbf{a}\]可得
\[\frac{\partial [ \mathbf{w}_i^T \mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i + \lambda (\mathbf{w}_i^T \mathbf{I} - 1) ]}{ \partial \mathbf{w}_i} = 2\mathbf{X}_i^T\mathbf{X}_i\mathbf{w}_i+\lambda \mathbf{I}=0\] \[\mathbf{X}_i^T \mathbf{X}_i \mathbf{w}_i=-\frac{1}{2}\lambda \mathbf{I}\]若$\mathbf{X}_i^T \mathbf{X}_i$可逆,则
\[\mathbf{w}_i=-\frac{1}{2}\lambda (\mathbf{X}_i^T \mathbf{X}_i)^{-1} \mathbf{I}\]又因为$\mathbf{w}_i^T \mathbf{I}= \mathbf{I}^T \mathbf{w}_i = 1$,则上式两边同时左乘$\mathbf{I}^T$可得
\[\mathbf{I}^T \mathbf{w}_i=-\frac{1}{2}\lambda \mathbf{I}^T (\mathbf{X}_i^T \mathbf{X}_i)^{-1} \mathbf{I} = 1\] \[-\frac{1}{2} \lambda = \frac{1}{\mathbf{I}^T (\mathbf{X}_i^T \mathbf{X}_i)^{-1} \mathbf{I}}\]将其代回$\mathbf{w}_i=-\frac{1}{2}\lambda (\mathbf{X}_i^T \mathbf{X}_i)^{-1} \mathbf{I}$即可解得
\[\mathbf{w}_i = \frac{(\mathbf{X}_i^T \mathbf{X}_i)^{-1} \mathbf{I}}{\mathbf{I}^T (\mathbf{X}_i^T \mathbf{X}_i)^{-1} \mathbf{I}}\]若令矩阵$(\mathbf{X}_i^T \mathbf{X}_i)^{-1}$第$j$行第$k$列的元素为$C_{jk}^{-1}$,则
\[w_{ij}=w_{iq_i^j}=\frac{\sum_{k\in Q_i} C_{jk}^{-1}}{\sum_{l,s \in Q_i} C_{ls}^{-1}}\]此即为公式(10.28)。显然,若$\mathbf{X}_i^T \mathbf{X}_i$可逆,此优化问题即为凸优化问题,且此时用拉格朗日乘子法求得的$\mathbf{w}_i$为全局最优解。
3.2.式(10.31)的推导
\[\begin{align} \min \limits_{\mathbf{Z}} \sum_{i=1}^m \parallel \mathbf{z}_i - \sum_{j \in Q_i} w_{ij} \mathbf{z}_j \parallel _2^2 &= \sum_{i=1}^m \parallel \mathbf{ZI}_i-\mathbf{ZW}_i \parallel_2^2 \\&= \sum_{i=1}^m \parallel \mathbf{Z} (\mathbf{I}_i-\mathbf{W}_i) \parallel_2^2 \\&= \sum_{i=1}^m (\mathbf{Z} (\mathbf{I}_i-\mathbf{W}_i))^T \mathbf{Z} (\mathbf{I}_i-\mathbf{W}_i) \\&= \sum_{i=1}^m (\mathbf{I}_i-\mathbf{W}_i)^T \mathbf{Z}^T \mathbf{Z} (\mathbf{I}_i-\mathbf{W}_i) \\&= \text{tr} ( (\mathbf{I}-\mathbf{W})^T \mathbf{Z}^T \mathbf{Z} (\mathbf{I}-\mathbf{W}) ) \\&= \text{tr} ( \mathbf{Z} (\mathbf{I}-\mathbf{W})(\mathbf{I}-\mathbf{W})^T \mathbf{Z}^T ) \\&= \text{tr} (\mathbf{ZMZ}^T) \\ \end{align}\]其中,
\[\mathbf{Z} = \begin{bmatrix} \mathbf{z}_1 & \mathbf{z}_2 & \cdots & \mathbf{z}_m \end{bmatrix} = \begin{bmatrix} z_{11} & z_{12} & \cdots & z_{1m} \\ z_{21} & z_{22} & \cdots & z_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ z_{d'1} & z_{d'2} & \cdots & z_{d'm} \end{bmatrix} \in \mathbb{R}^{d'\times m}\]每一列为一个样本,一共有$m$个样本。此外还有,
\[\mathbf{I}= \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{bmatrix} \in \mathbb{R}^{m\times m}, \mathbf{I}_i \in \mathbb{R}^{m\times 1}\] \[\mathbf{W}=\begin{bmatrix} w_{11} & w_{21} & \cdots & w_{m1} \\ w_{12} & w_{22} & \cdots & w_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ w_{m1} & w_{2m} & \cdots & w_{mm} \\ \end{bmatrix} \in \mathbb{R}^{m\times m}, \mathbf{W}_i \in \mathbb{R}^{m \times 1}\]$\mathbf{W}$其实是个稀疏矩阵。举个例子,假设$\mathbf{z}_1=w_{12}\mathbf{z}_2+w_{13}\mathbf{z}_3+w_{14}\mathbf{z}_4$,那么其对应的:
\[\mathbf{W}_1 = \begin{bmatrix} 0 \\ w_{12} \\ w_{13} \\ w_{14} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \in \mathbb{R}^{m\times 1}\]关于矩阵的迹,有:
\[\text{tr} (AA^T) = \text{tr} (A^TA)\]根据推导,
\[\mathbf{M}=(\mathbf{I}-\mathbf{W})(\mathbf{I}-\mathbf{W})^T\]个人理解:式(10.30)应该以此处的为准,原书应该是写错了。
约束条件$\mathbf{Z} \mathbf{Z}^T=\mathbf{I}$是为了得到标准化(标准正交空间)的低维数据(此处的$\mathbf{I}$应该是$d’ \times d’$的单位矩阵)。
用拉格朗日乘子法求$\mathbf{Z}$:
\[L(\mathbf{Z},\lambda)=\mathbf{ZMZ}^T + \lambda (\mathbf{Z}\mathbf{Z}^T - \mathbf{I})\] \[\frac{\partial L(\mathbf{Z},\lambda)}{\partial \mathbf{Z}}=2 \mathbf{MZ}^T+2\lambda \mathbf{Z}^T=0\]从而得到,
\[\mathbf{MZ}^T=-\lambda \mathbf{Z}^T = \lambda' \mathbf{Z}^T\]因此,$\mathbf{Z}^T$是矩阵$M$的特征向量组成的矩阵。把$\mathbf{MZ}^T=-\lambda \mathbf{Z}^T $代入:
\[\begin{align} L(\mathbf{Z},\lambda) &= \mathbf{ZMZ}^T + \lambda (\mathbf{Z}\mathbf{Z}^T - \mathbf{I}) \\&= -\lambda \mathbf{I} \\&= \lambda' \mathbf{I} \end{align}\]若要求$L(\mathbf{Z},\lambda)$最小,则$\lambda ^{‘}$最小,即取$\mathbf{M}$的最小特征值。