博客为参考《啊哈!算法》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.不撞南墙不回头——深度优先搜索
在第三章第4部分我们留下了一个问题:输入一个数n,输出1~n的全排列。这里我们先将这个问题形象化,举个例子。假如有编号为1、2、3的3张扑克牌和编号为1、2、3的3个盒子。现在需要将这3张扑克牌分别放到3个盒子里面,并且每个盒子有且只能放一张扑克牌。那么一共有多少种不同的放法呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
int a[10]={0,0,0,0,0,0,0,0,0,0}, book[10]={0,0,0,0,0,0,0,0,0,0}, n=0;
void dfs(int step) //step表示现在站在第几个盒子面前
{
int i;
if(step == n+1) //如果站在第n+1个盒子面前,则表示前n个盒子已经放好扑克牌
{
//输出一种排列(1~n号盒子中的扑克牌编号)
for(i=1; i<=n; i++)
printf("%d",a[i]);
printf("\n");
return; //返回之前的一步(最近一次调用dfs函数地方)
}
//此时站在第step个盒子面前,应该放哪张牌呢?
//按照1、2、3、...、n的顺序一一尝试
for(i=1; i<=n; i++)
{
//判断扑克牌i是否还在手上
if(book[i]==0) //book[i]等于0表示i号扑克牌在手上
{
//开始尝试使用扑克牌i
a[step]=i; //将i号扑克牌放入到第step个盒子中
book[i]=1; //将book[i]设为1,表示i号扑克牌已经不在手上
//第step个盒子已经放好扑克牌,接下来需要走到下一个盒子面前
dfs(step+1); //这里通过函数的递归调用来实现(自己调用自己)
book[i]=0; //这是非常重要的一步,一定要将刚才尝试的扑克牌收回,才能进行下一次尝试
}
}
return;
}
int main()
{
scanf("%d",&n); //输入的时候要注意n为1~9之间的整数
dfs(1); //首先站在1号小盒子面前
getchar();getchar();
return 0;
}
上述代码饱含深度优先搜索(Depth First Search,DFS)的基本模型。下面的代码就是深度优先搜索的基本模型:
1
2
3
4
5
6
7
8
9
10
void dfs(int step)
{
//判断边界
for(i = 1; i <= n; i++) //尝试每一种可能
{
//继续下一步
dfs(step+1);
}
//返回
}
现在我们可以用DFS算法来解第三章第1部分提出的问题了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <stdio.h>
int a[10]={0,0,0,0,0,0,0,0,0,0}, book[10]={0,0,0,0,0,0,0,0,0,0}, total=0;
void dfs(int step) //step表示现在站在第几个盒子面前
{
int i;
if(step == 10) //如果站在第10个盒子面前,则表示前9个盒子已经放好扑克牌
{
//判断是否满足等式???+???=???
if(a[1]*100+a[2]*10+a[3]+a[4]*100+a[5]*10+a[6]==a[7]*100+a[8]*10+a[9])
{
//如果满足要求,可行解+1,并打印这个解
total++;
printf("%d%d%d+%d%d%d=%d%d%d\n",a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]);
}
return; //返回之前的一步(最近调用的地方)
}
//此时站在第step个盒子面前,应该放哪张牌呢?
//按照1、2、3、...、n的顺序一一尝试
for(i=1; i<=9; i++)
{
//判断扑克牌i是否还在手上
if(book[i]==0) //book[i]等于0表示i号扑克牌在手上
{
//开始尝试使用扑克牌i
a[step]=i; //将i号扑克牌放入到第step个盒子中
book[i]=1; //将book[i]设为1,表示i号扑克牌已经不在手上
//第step个盒子已经放好扑克牌,接下来需要走到下一个盒子面前
dfs(step+1); //这里通过函数的递归调用来实现(自己调用自己)
book[i]=0; //这是非常重要的一步,一定要将刚才尝试的扑克牌收回,才能进行下一次尝试
}
}
return;
}
int main()
{
dfs(1); //首先站在一个盒子面前
printf("total=%d",total/2);
getchar();getchar();
return 0;
}
2.解救小哈
假设有一个由n行m列个单元格组成的迷宫(n和m都小于等于50),每个单元格要么是空地,要么是障碍物。我们的任务是帮助小哼找到一条从迷宫起点通往小哈所在位置的最短路径。注意障碍物是不能走的,当然小哼也不能走到迷宫之外。
我们可以用一个二维数组来存储这个迷宫。现在我们尝试用深度优先搜索来实现这个方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>
int n,m,p,q,min=99999999;
int a[51][51],book[51][51];
void dfs(int x, int y, int step)
{
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
int tx,ty,k;
//判断是否到达小哈的位置
if(x==p && y==q)
{
//更新最小值
if(step<min)
min=step;
return;//请注意这里的返回很重要
}
//枚举4种走法
for(k=0;k<=3;k++)
{
//计算下一个点的坐标
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1 || tx>n || ty<1 || ty>m)
continue;
//判断该点是否为障碍物或者已经在路径中
if(a[tx][ty]==0 && book[tx][ty]==0)
{
book[tx][ty]=1;//标记这个点已经走过
dfs(tx,ty,step+1);//开始尝试下一个点
book[tx][ty]=0;//尝试结束,取消这个点的标记
}
}
return;
}
int main()
{
int i,j,startx,starty;
//读入n和m,n为行,m为列
scanf("%d %d",&n,&m);
//读入迷宫
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&a[i][j]);
//读入起点和终点坐标
scanf("%d %d %d %d",&startx,&starty,&p,&q);
//从起点开始搜索
book[startx][starty]=1;//标记起点已经在路径中,防止后面重复走
//第一个参数是起点的x坐标,第二个参数是起点的y坐标,第三个参数是初始步数为0
dfs(startx,starty,0);
//输出最短步数
printf("%d",min);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。第一行有两个数n、m。n表示迷宫的行,m表示迷宫的列。接下来的n行m列为迷宫,0表示空地,1表示障碍物。最后一个4个数,前两个数为迷宫入口的x和y坐标。后两个为小哈的x和y坐标。
1
2
3
4
5
6
7
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
运行结果是:
1
7
3.层层递进——广度优先搜索
在上一部分,我们使用了深度优先搜索的方法。这里我们将介绍另外一种方法来解决这个问题——广度优先搜索(Breadth First Search,BFS),也称为宽度优先搜索。
我们还是用一个二维数组来存储这个迷宫。最开始的时候小哼在迷宫(1,1)处,他可以往右走或者往下走。在上一部分中我们的方法是,先让小哼往右边走,然后一直尝试下去,直到走不通的时候再回到这里。这样是深度优先,可以通过函数的递归实现。现在介绍另外一种方法:通过“一层一层”扩展的方法来找到小哈。扩展时每发现一个点就将这个点加入到队列中,直至走到小哈的位置(p,q)时为止,具体如下。
最开始小哼在入口(1,1)处,一步之内可以到达的点有(1,2)和(2,1)。

然后小哼继续前进,2步可以走到的点有(2,2)和(3,1),但依然没有找到小哈。
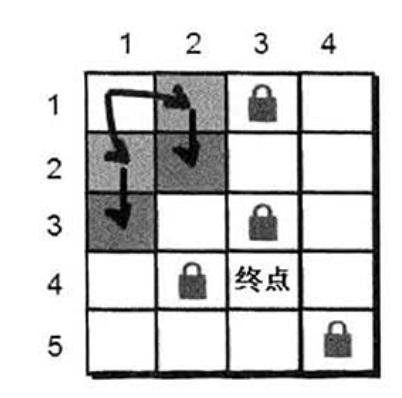
还得继续往下尝试,看看通过(2,2)和(3,1)这两个点还能到达哪些新的没有走到过的点。通过(2,2)这个点我们可以到达(2,3)和(3,2),通过(3,1)可以到达(3,2)和(4,1)。现在3步可以到达的点有(2,3)、(3,2)和(4,1),依旧没有到达小哈的所在点,我们需要重复刚才的方法,直到到达小哈所在点为止。
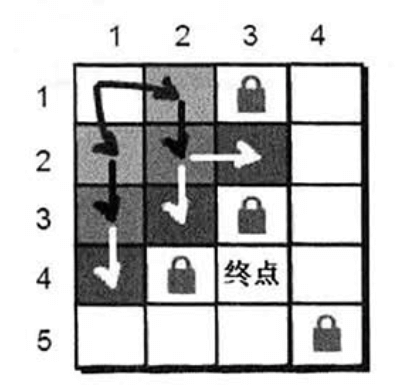
我们用队列来模拟这个过程:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include <stdio.h>
struct note
{
int x;
int y;
int f;//父亲在队列中的编号
int s;//步数
};
int main()
{
struct note que[2501];//假设地图大小不超过50*50
int a[51][51]={0},book[51][51]={0};
//定义一个用于表示走的方向的数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
int head,tail;
int i,j,k,n,m,startx,starty,p,q,tx,ty,flag;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&a[i][j]);
scanf("%d %d %d %d",&startx,&starty,&p,&q);
//队列初始化
head=1;
tail=1;
//往队列插入迷宫入口坐标
que[tail].x=startx;
que[tail].y=starty;
que[tail].f=0;
que[tail].s=0;
tail++;
book[startx][starty]=1;
flag=0;//用来标记是否到达目标点,0表示暂时还没有到达,1表示到达
//当队列不为空的时候循环
while(head<tail)
{
//枚举4个方向
for(k=0;k<=3;k++)
{
//计算下一个点的坐标
tx=que[head].x+next[k][0];
ty=que[head].y+next[k][1];
//判断是否越界
if(tx<1 || tx>n || ty<1 || ty>m)
continue;;
//判断是否是障碍物或者已经在路径中
if(a[tx][ty]==0 && book[tx][ty]==0)
{
//把这个点标记为已经走过
//注意宽搜每个点只入队一次,所以和深搜不同,不需要将book数组还原
book[tx][ty]=1;
//插入新的点到队列中
que[tail].x=tx;
que[tail].y=ty;
que[tail].f=head;
que[tail].s=que[head].s+1;//步数是父亲的步数+1
tail++;
}
//如果到目标点了,停止扩展,任务结束,退出循环
if(tx==p && ty==q)
{
flag=1;
break;
}
}
if(flag==1)
break;
head++;//注意这地方千万不要忘记,当一个点扩展结束后,head++才能对后面的点再进行扩展
}
//打印队列中末尾最后一个点(目标点)的步数
//注意tail是指向队列队尾(即最后一位)的下一个位置,所以这需要-1
printf("%d",que[tail-1].s);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。第一行有两个数n和m。n表示迷宫的行,m表示迷宫的列。接下来n行m列为迷宫,0表示空地,1表示障碍物。最后一行4个数,前两个数为迷宫入口的x和y坐标。后两个为小哈的x和y坐标。
1
2
3
4
5
6
7
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
运行结果是:
1
7
4.再解炸弹人
第三章第2部分留下的问题:

按照第三章第2部分的方法,将炸弹放置在(1,11)处,最多可以消灭11个敌人(注意这里是从0行0列开始计算的)。但小人其实是无法走到(1,11)的。所以正确的答案应该是将炸弹放在(7,11)处,可以消灭10个敌人。我们可以使用本章学习的广度优先搜索或者深度优先搜索来解决这个问题。
广度优先搜索的实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include <stdio.h>
struct note
{
int x;
int y;
};
char a[20][20];//用来存储地图
int getnum(int i, int j)
{
int sum,x,y;
sum=0;//sum用来计数(可以消灭的敌人数),所以需要初始化为0
//将坐标i,j复制到两个新变量x,y中,以便之后向上下左右四个方向统计可以消灭的敌人数
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
x--;
}
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
x++;
}
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
y--;
}
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
y++;
}
return sum;
}
int main()
{
struct note que[401];//假设地图大小不超过20*20
int head,tail;
int book[20][20]={0};//定义一个标记数组并全部初始化为0
int i,j,k,sum,max=0,mx,my,n,m,startx,starty,tx,ty;
//定义一个用于表示走的方向的数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
//n行m列
scanf("%d %d %d %d",&n,&m,&startx,&starty);
//读入n行字符
for(i=0;i<=n-1;i++)
scanf("%s",a[i]);
//队列初始化
head=1;
tail=1;
//往队列插入小人的起始坐标
que[tail].x=startx;
que[tail].y=starty;
tail++;
book[startx][starty]=1;
max=getnum(startx, starty);
mx=startx;
my=starty;
//当队列不为空的时候循环
while(head<tail)
{
//枚举4个方向
for(k=0;k<=3;k++)
{
//尝试走的下一个点的坐标
tx=que[head].x+next[k][0];
ty=que[head].y+next[k][1];
//判断是否越界
if(tx<0 || tx>n-1 || ty<0 || ty>m-1)
continue;
//判断是否为平地或者曾经走过
if(a[tx][ty]=='.' && book[tx][ty]==0)
{
//每个点只入队一次,所以需要标记这个点已经走过
book[tx][ty]=1;
//插入新扩展的点到队列中
que[tail].x=tx;
que[tail].y=ty;
tail++;
//统计当前新扩展的点可以消灭的敌人总数
sum=getnum(tx, ty);
//更新max的值
if(sum>max)
{
max=sum;
mx=tx;
my=ty;
}
}
}
head++;
}
printf("将炸弹放置在(%d,%d)处,可以消灭%d个敌人\n",mx,my,max);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
13 13 3 3
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.#.#
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############
运行结果是:
1
将炸弹放置在(7,11)处,可以消灭10个敌人
当然也可以用深度优先搜索来做:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <stdio.h>
char a[20][20];//用来存储地图
int book[20][20],max,mx,my,n,m;
int getnum(int i, int j)
{
int sum,x,y;
sum=0;//sum用来计数(可以消灭的敌人数),所以需要初始化为0
//将坐标i,j复制到两个新变量x,y中,以便之后向上下左右四个方向统计可以消灭的敌人数
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
x--;
}
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
x++;
}
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
y--;
}
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前的点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
y++;
}
return sum;
}
void dfs(int x,int y)
{
//定义一个用于表示走的方向的数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
int k,sum,tx,ty;
//计算当前这个点可以消灭的敌人总数
sum=getnum(x, y);
//更新max的值
if(sum>max)
{
max=sum;
mx=x;
my=y;
}
//枚举4个方向
for(k=0;k<=3;k++)
{
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<0 || tx>n-1 || ty<0 || ty>m-1)
continue;
if(a[tx][ty]=='.' && book[tx][ty]==0)
{
book[tx][ty]=1;//标记这个点已走过
dfs(tx,ty);//开始尝试下一个点
}
}
return;
}
int main()
{
int i,startx,starty;
//n行m列
scanf("%d %d %d %d",&n,&m,&startx,&starty);
//读入n行字符
for(i=0;i<=n-1;i++)
scanf("%s",a[i]);
//从小人所站的位置开始尝试
book[startx][starty]=1;
max=getnum(startx, starty);
mx=startx;
my=starty;
dfs(startx, starty);
printf("将炸弹放置在(%d,%d)处,可以消灭%d个敌人\n",mx,my,max);
getchar();getchar();
return 0;
}
5.宝岛探险
我们用一个$10\times 10$的二维矩阵表示地图,图中的数字表示海拔,0表示海洋,1~9都表示陆地。小哼的飞机将会降落在(6,8)处,现在需要计算出小哼降落地所在岛的面积(即有多少个格子)。注意此处我们把与小哼降落点上下左右相连接的陆地均视为同一岛屿。
使用广度优先搜索的实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <stdio.h>
struct note
{
int x;
int y;
};
int main()
{
struct note que[2501];//假设地图大小不超过50*50
int head,tail;
int a[51][51];
int book[51][51]={0};
int i,j,k,sum,max=0,mx,my,n,m,startx,starty,tx,ty;
//定义一个方向数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
//读入n行m列以及小哼降落的坐标
scanf("%d %d %d %d",&n,&m,&startx,&starty);
//读入地图
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
//队列初始化
head=1;
tail=1;
//往队列插入降落的起始坐标
que[tail].x=startx;
que[tail].y=starty;
tail++;
book[startx][starty]=1;
sum=1;
//当队列不为空的时候循环
while(head<tail)
{
//枚举4个方向
for(k=0;k<=3;k++)
{
//计算下一步的坐标
tx=que[head].x+next[k][0];
ty=que[head].y+next[k][1];
//判断是否越界
if(tx<1 || tx>n || ty<1 || ty>m)
continue;
//判断是否是陆地或者曾经是否走过
if(a[tx][ty]>0 && book[tx][ty]==0)
{
sum++;
//每个点只入队一次,所以需要标记这个点已经走过
book[tx][ty]=1;
//将新扩展的点加入队列
que[tail].x=tx;
que[tail].y=ty;
tail++;
}
}
head++;
}
//最后输出岛屿的大小
printf("%d\n",sum);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。第一行4个整数分别表示地图的行和列,以及降落的初始坐标。接下来的n行m列为地图。
1
2
3
4
5
6
7
8
9
10
11
10 10 6 8
1 2 1 0 0 0 0 0 2 3
3 0 2 0 1 2 1 0 1 2
4 0 1 0 1 2 3 2 0 1
3 2 0 0 0 1 2 4 0 0
0 0 0 0 0 0 1 5 3 0
0 1 2 1 0 1 5 4 3 0
0 1 2 3 1 3 6 2 1 0
0 0 3 4 8 9 7 5 0 0
0 0 0 3 7 8 6 0 1 2
0 0 0 0 0 0 0 0 1 0
运行结果是:
1
38
当然也可以用深度优先搜索的方法来做,代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>
int a[51][51];
int book[51][51],n,m,sum;
void dfs(int x, int y)
{
//定义一个方向数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
int k,tx,ty;
//枚举4个方向
for(k=0;k<=3;k++)
{
//计算下一步的坐标
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1 || tx>n || ty<1 || ty>m)
continue;
//判断是否是陆地
if(a[tx][ty]>0 && book[tx][ty]==0)
{
sum++;
book[tx][ty]=1;//标记这个点已走过
dfs(tx,ty);//开始尝试下一个点
}
}
return;
}
int main()
{
int i,j,startx,starty;
scanf("%d %d %d %d",&n,&m,&startx,&starty);
//读入地图
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
book[startx][starty]=1;
sum=1;
//从降落的位置开始
dfs(startx, starty);
//最后输出岛屿的大小
printf("%d\n",sum);
getchar();getchar();
return 0;
}
上面这种方法又叫做着色法:以某个点为源点对其邻近的点进行着色。比如我们可以将上面的代码稍加改动,将小哼降落的岛都改为-1,表示该岛已经被小哼玩遍了。
要实现这个需求只需在dfs()函数中加一个参数color就可以了,color表示该岛屿所需要染的颜色:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
int a[51][51];
int book[51][51],n,m,sum;
void dfs(int x, int y, int color)
{
//定义一个方向数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
int k,tx,ty;
a[x][y]=color;//对a[x][y]这个格子进行染色
//枚举4个方向
for(k=0;k<=3;k++)
{
//计算下一步的坐标
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1 || tx>n || ty<1 || ty>m)
continue;
//判断是否是陆地
if(a[tx][ty]>0 && book[tx][ty]==0)
{
sum++;
book[tx][ty]=1;//标记这个点已走过
dfs(tx,ty,color);//开始尝试下一个点
}
}
return;
}
int main()
{
int i,j,startx,starty;
scanf("%d %d %d %d",&n,&m,&startx,&starty);
//读入地图
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
book[startx][starty]=1;
sum=1;
//从降落的位置开始
dfs(startx, starty,-1);
//输出已经染色后的地图
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
printf("%3d",a[i][j]);
}
printf("\n");
}
getchar();getchar();
return 0;
}
可以输入以下数据进行验证:
1
2
3
4
5
6
7
8
9
10
11
10 10 6 8
1 2 1 0 0 0 0 0 2 3
3 0 2 0 1 2 1 0 1 2
4 0 1 0 1 2 3 2 0 1
3 2 0 0 0 1 2 4 0 0
0 0 0 0 0 0 1 5 3 0
0 1 2 1 0 1 5 4 3 0
0 1 2 3 1 3 6 2 1 0
0 0 3 4 8 9 7 5 0 0
0 0 0 3 7 8 6 0 1 2
0 0 0 0 0 0 0 0 1 0
运行结果是:
1
2
3
4
5
6
7
8
9
10
1 2 1 0 0 0 0 0 2 3
3 0 2 0 -1 -1 -1 0 1 2
4 0 1 0 -1 -1 -1 -1 0 1
3 2 0 0 0 -1 -1 -1 0 0
0 0 0 0 0 0 -1 -1 -1 0
0 -1 -1 -1 0 -1 -1 -1 -1 0
0 -1 -1 -1 -1 -1 -1 -1 -1 0
0 0 -1 -1 -1 -1 -1 -1 0 0
0 0 0 -1 -1 -1 -1 0 1 2
0 0 0 0 0 0 0 0 1 0
如果想知道这个地图中有多少个独立的小岛又该怎么做呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <stdio.h>
int a[51][51];
int book[51][51],n,m,sum;
void dfs(int x, int y, int color)
{
//定义一个方向数组
int next[4][2] = {
{0,1},
{1,0},
{0,-1},
{-1,0}
};
int k,tx,ty;
a[x][y]=color;//对a[x][y]这个格子进行染色
//枚举4个方向
for(k=0;k<=3;k++)
{
//计算下一步的坐标
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1 || tx>n || ty<1 || ty>m)
continue;
//判断是否是陆地
if(a[tx][ty]>0 && book[tx][ty]==0)
{
sum++;
book[tx][ty]=1;//标记这个点已走过
dfs(tx,ty,color);//开始尝试下一个点
}
}
return;
}
int main()
{
int i,j,num=0;
scanf("%d %d",&n,&m);
//读入地图
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
//对每一个大于0的点尝试进行dfs染色
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if(a[i][j]>0)
{
num--;//小岛需要染的颜色的编号
//每发现一个小岛应染以不同的颜色,因此每次要-1
book[i][j]=1;
dfs(i, j, num);
}
}
}
//输出已经染色后的地图
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
printf("%3d",a[i][j]);
}
printf("\n");
}
//输出小岛的个数
printf("有%d个小岛\n",-num);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。
1
2
3
4
5
6
7
8
9
10
11
10 10
1 2 1 0 0 0 0 0 2 3
3 0 2 0 1 2 1 0 1 2
4 0 1 0 1 2 3 2 0 1
3 2 0 0 0 1 2 4 0 0
0 0 0 0 0 0 1 5 3 0
0 1 2 1 0 1 5 4 3 0
0 1 2 3 1 3 6 2 1 0
0 0 3 4 8 9 7 5 0 0
0 0 0 3 7 8 6 0 1 2
0 0 0 0 0 0 0 0 1 0
运行结果如下:
1
2
3
4
5
6
7
8
9
10
11
-1 -1 -1 0 0 0 0 0 -2 -2
-1 0 -1 0 -3 -3 -3 0 -2 -2
-1 0 -1 0 -3 -3 -3 -3 0 -2
-1 -1 0 0 0 -3 -3 -3 0 0
0 0 0 0 0 0 -3 -3 -3 0
0 -3 -3 -3 0 -3 -3 -3 -3 0
0 -3 -3 -3 -3 -3 -3 -3 -3 0
0 0 -3 -3 -3 -3 -3 -3 0 0
0 0 0 -3 -3 -3 -3 0 -4 -4
0 0 0 0 0 0 0 0 -4 0
有4个小岛
其实这就是求一个图中独立子图的个数。这个算法就是Floodfill漫水填充法(也称种子填充法)。Floodfill在计算机图形学中有着非常广泛的运用,比如图像分割、物体识别等等。另外我们熟知的Windows下“画图”软件的油漆桶工具就是基于这个算法的。
6.水管工游戏
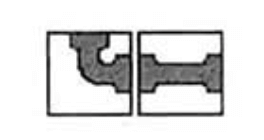
假设水管只有2种,如下图所示:
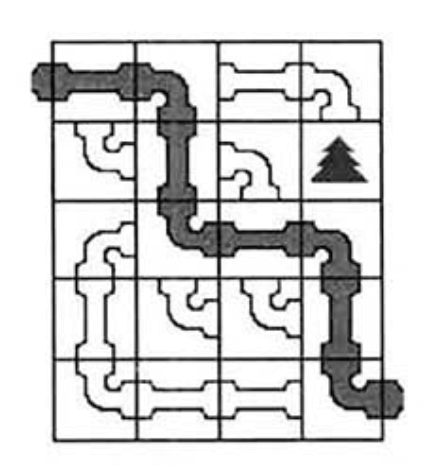
每种管道将占据一个单位正方形土地。你现在可以旋转这些管道,使其构成一个管道系统,即创造一条从(1,1)到(N,M)的连通管道。标有树木的方格表示这里没有管道。如下图表示一个5*4的土地中(2,4)处有一个树木。

我们可以旋转其中的一些管道,使之构成一个连通的管道系统,如下图。
如果通过旋转管道可以使之构成一个连通的管道系统,就输出铺设的路径,否则输出impossible。例如输入如下数据。
1
2
3
4
5
6
5 4
5 3 5 3
1 5 3 0
2 3 5 1
6 1 1 5
1 5 5 4
输出:
1
(1,1) (1,2) (2,2) (3,2) (3,3) (3,4) (4,4) (5,4)
输入的第一行为两个整数N和M(都不超过10),接下来的N行,每行有M个整数,表示地图中的每一小格。其中0表示树木,1~6分别表示管道的六种不同的摆放方式,如下图。
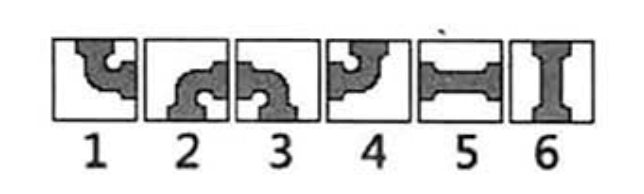
因为只有两种水管,一种是弯管一种是直管。弯管有4种状态,直管有2种状态。
我们仍然可以使用深度优先搜索来解决。当处在第x行第y列格子的时候,需要依此枚举当前管道的每一张摆放方式,直管有2种,弯管有4种。此处并不是每一种都可以,还需要判断进水口的方向才行,为了后面程序处理方便,这里将进水口在左边用1表示,进水口在上边用2表示,进水口在右边用3表示,进水口在下边用4表示。完整代码实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <stdio.h>
int a[51][51];//假设土地的大小不超过50*50
int book[51][51],n,m,flag=0;
struct note
{
int x;
int y;
} s[100];
int top=0;
void dfs(int x, int y, int front)
{
int i;
//判断是否到达终点
if(x==n && y==m+1)
{
flag=1;//找到铺设方案
for(i=1;i<=top;i++)
printf("(%d,%d) ",s[i].x,s[i].y);
return;
}
//判断是否越界
if(x<1 || x>n || y<1 || y>m)
return;
//判断这个管道是否在路径中已经使用过
if(book[x][y]==1)
return;
book[x][y]=1;//标记使用当前这个管道
//将当前尝试的坐标入栈
top++;
s[top].x=x;
s[top].y=y;
//当前水管是直管的情况
if(a[x][y]>=5 && a[x][y]<=6)
{
if(front==1)//进水口在左边的情况
dfs(x,y+1,1);//只能使用5号这种摆放方式
if(front==2)//进水口在上边的情况
dfs(x+1,y,2);//只能使用6号这种摆放方式
if(front==3)//进水口在右边的情况
dfs(x,y-1,3);//只能使用5号这种摆放方式
if(front==4)//进水口在下边的情况
dfs(x-1,y,4);//只能使用6号这种摆放方式
}
//当前水管是弯管的情况
if(a[x][y]>=1 && a[x][y]<=4)
{
if(front==1)
{
dfs(x+1,y,2);//3号状态
dfs(x-1,y,4);//4号状态
}
if(front==2)
{
dfs(x,y+1,1);//1号状态
dfs(x,y-1,3);//4号状态
}
if(front==3)
{
dfs(x-1,y,4);//1号状态
dfs(x+1,y,2);//2号状态
}
if(front==4)
{
dfs(x,y+1,1);//2号状态
dfs(x,y-1,3);//3号状态
}
}
book[x][y]=0;//取消标记
top--;//将当前尝试的坐标出栈
return;
}
int main()
{
int i,j,num=0;
scanf("%d %d",&n,&m);
//读入游戏地图
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&a[i][j]);
//开始搜索,从1,1点开始,进水方向也是1
dfs(1,1,1);
//判断是否找到铺设方案
if(flag==0)
printf("impossible\n");
getchar();getchar();
return 0;
}