本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.python实现PCA
1.1.主成分分析
1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
print(X.shape) #(150, 4)
pca = PCA(n_components=2)
pca.fit(X)
X_reduced = pca.transform(X)
print(X_reduced.shape) #(150, 2)
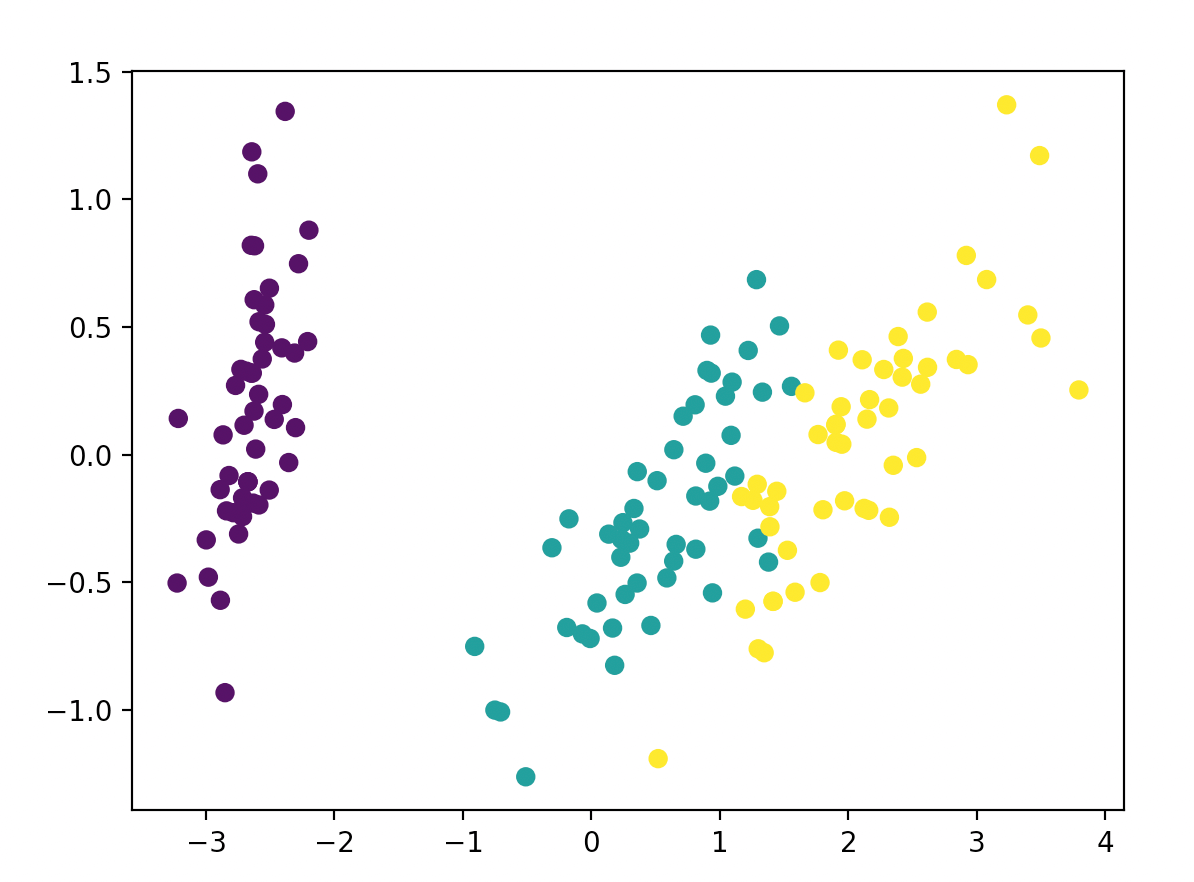
1.2.根据主成分绘制散点图
1
2
3
from matplotlib import pyplot as plt
plt.scatter(X_reduced[:,0], X_reduced[:,1], c=y)
plt.show()
1.3.主成分组成
1
2
3
print(pca.components_)
for component in pca.components_:
print(" + ".join("%.3f x %s" % (value,name) for value,name in zip(component, iris.feature_names)))
输出为:
1
2
3
4
[[ 0.36158968 -0.08226889 0.85657211 0.35884393]
[ 0.65653988 0.72971237 -0.1757674 -0.07470647]]
0.362 x sepal length (cm) + -0.082 x sepal width (cm) + 0.857 x petal length (cm) + 0.359 x petal width (cm)
0.657 x sepal length (cm) + 0.730 x sepal width (cm) + -0.176 x petal length (cm) + -0.075 x petal width (cm)
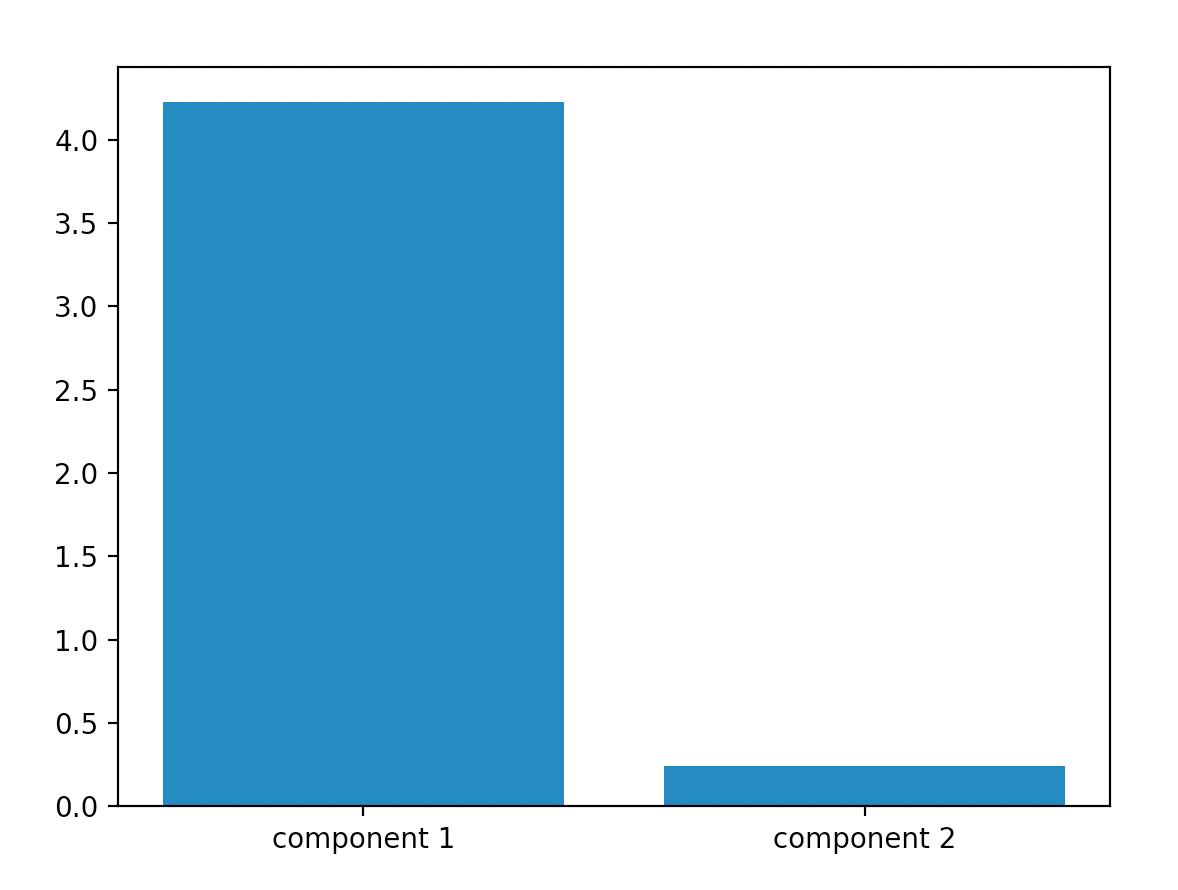
1.4.变异数解释量
输出主成分的可解释程度,一般会选择可解释度大于1的主成分。
1
2
3
plt.bar(range(0,2), pca.explained_variance_)
plt.xticks(range(0,2),["component 1","component 2"])
plt.show()