博客为参考《啊哈!算法》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.深度和广度优先究竟是指啥
深度和广度是针对图的遍历而言的,请见下图:
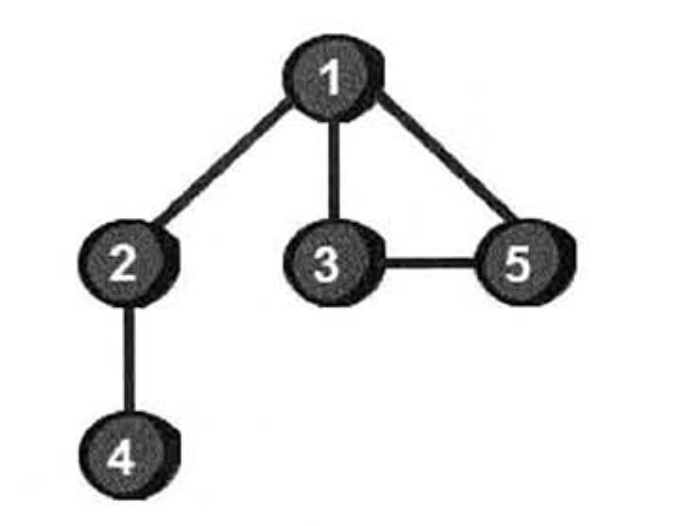
图由顶点和边组成。现在我们从1号顶点开始遍历这个图。使用深度优先搜索来遍历这个图将会得到如下的结果。
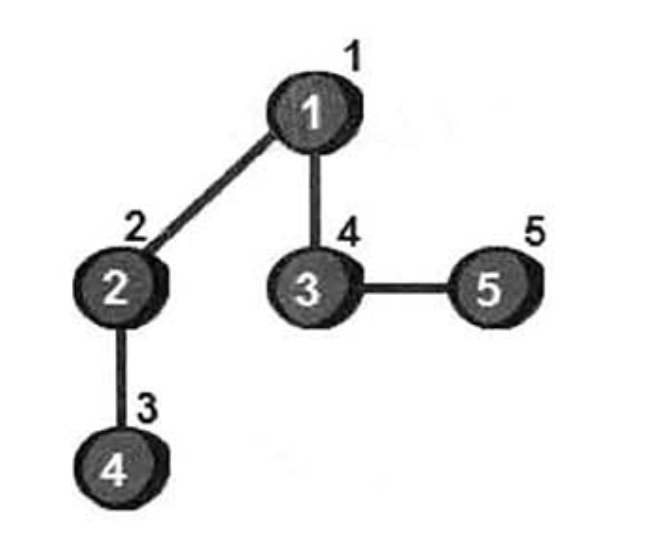
图中每个顶点右上方的数就表示这个顶点是第几个被访问到的,我们将这个数称为时间戳。
我们使用一个二维数组e来存储图,如下。
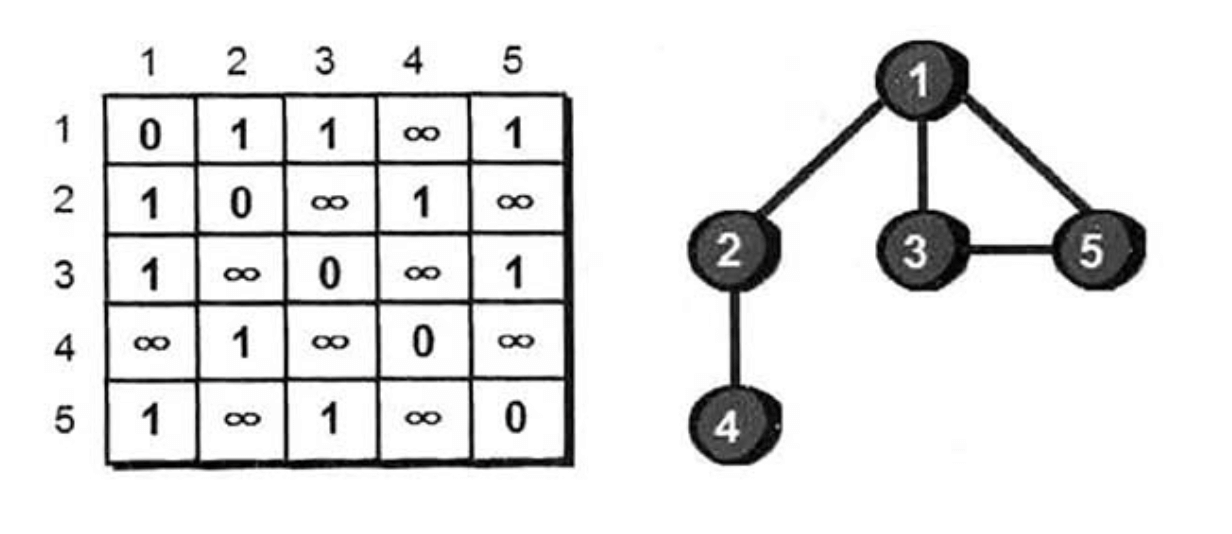
上图二维数组中第i行第j列表示的就是顶点i到顶点j是否有边。1表示有边,$\infty$表示没有边,将自己到自己(即i等于j)设为0。我们将这种存储图的方法称为图的邻接矩阵存储法。
这个二维数组是沿主对角线对称的,因为上面这个图是无向图。所谓无向图指的就是图的边没有方向,例如边1-5表示,1号顶点可以到5号顶点,5号顶点也可以到1号顶点。完整的代码实现见下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <stdio.h>
int book[101],sum,n,e[101][101];
void dfs(int cur) //cur是当前所在的顶点编号
{
int i;
printf("%d ",cur);
sum++; //每访问一个顶点,sum就加1
if(sum==n) return; //所有的顶点都已经访问过则直接退出
for(i=1;i<=n;i++) //从1号顶点到n号顶点依次尝试,看哪些顶点与当前顶点cur有边相连
{
//判断当前顶点cur到顶点i是否有边,并判断顶点i是否已访问过
if(e[cur][i]==1 && book[i]==0)
{
book[i]=1; //标记顶点i已经访问过
dfs(i); //从顶点i再出发继续遍历
}
}
return;
}
int main()
{
int i,j,m,a,b;
scanf("%d %d",&n,&m);
//初始化二维矩阵
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=99999999; //我们这里假设99999999为正无穷
//读入顶点之间的边
for(i=1;i<=m;i++)
{
scanf("%d %d",&a,&b);
e[a][b]=1;
e[b][a]=1; //这里是无向图,所以需要将e[b][a]也赋为1
}
//从1号顶点出发
book[1]=1; //标记1号顶点已访问
dfs(1); //从1号顶点开始遍历
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。
1
2
3
4
5
6
5 5
1 2
1 3
1 5
2 4
3 5
运行结果是:
1
1 2 4 3 5
使用广度优先搜索来遍历这个图的结果如下。
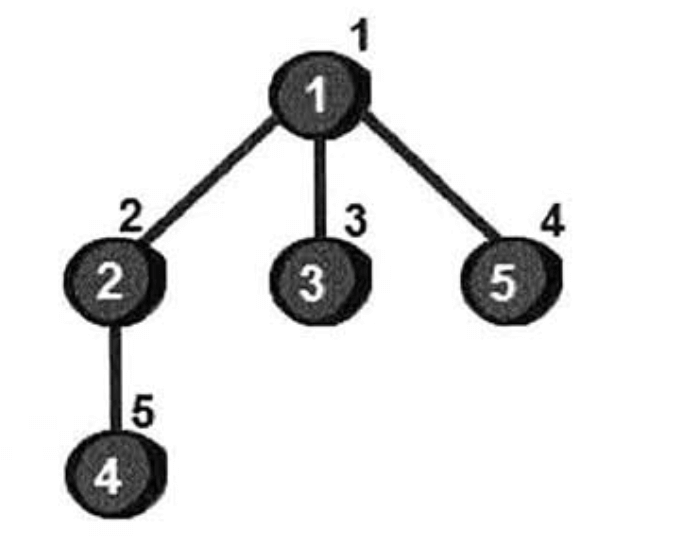
使用队列实现,代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <stdio.h>
int main()
{
int i,j,n,m,a,b,cur,book[101]={0},e[101][101];
int que[10001],head,tail;
scanf("%d %d",&n,&m);
//初始化二维矩阵
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=99999999; //我们这里假设99999999为正无穷
//读入顶点之间的边
for(i=1;i<=m;i++)
{
scanf("%d %d",&a,&b);
e[a][b]=1;
e[b][a]=1; //这里是无向图,所以需要将e[b][a]也赋值为1
}
//队列初始化
head=1;
tail=1;
//从1号顶点出发,将1号顶点加入队列
que[tail]=1;
tail++;
book[1]=1; //标记1号顶点已访问
//当队列不为空的时候循环
while(head<tail)
{
cur=que[head]; //当前正在访问的顶点编号
for(i=1;i<=n;i++) //从1~n依次尝试
{
//判断从顶点cur到顶点i是否有边,并判断顶点i是否已经访问过
if(e[cur][i]==1 && book[i]==0)
{
//如果从顶点cur到顶点i有边,并且顶点i没有被访问过,则将顶点i入队
que[tail]=i;
tail++;
book[i]=1; //标记顶点i已访问
}
//如果tail大于n,则表明所有顶点都已经被访问过
if(tail>n)
{
break;
}
}
head++; //注意这地方,千万不要忘记当一个顶点扩展结束后,head++,然后才能继续往下扩展
}
for(i=1;i<tail;i++)
printf("%d ",que[i]);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。
1
2
3
4
5
6
5 5
1 2
1 3
1 5
2 4
3 5
运行结果是:
1
1 2 3 5 4
使用深度优先搜索和广度优先搜索来遍历图都将会得到这个图的生成树。接下来我们看下图能解决什么实际问题。
2.城市地图——图的深度优先遍历
假设有城市地图如下。
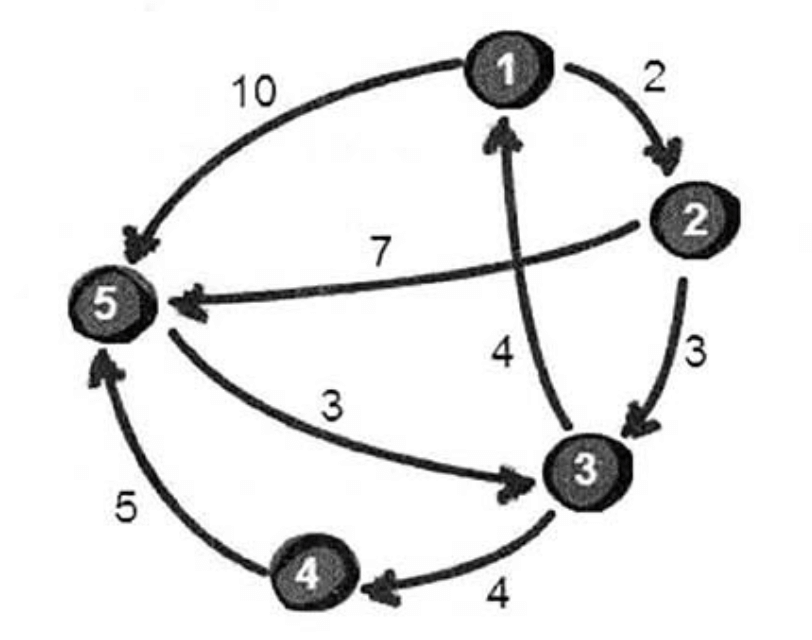
已知有5个城市和8条公路,求出1号城市到5号城市的最短路程(也叫做最短路径)。我们可以用一个5*5的矩阵(二维数组e)来存储这些信息,如下。
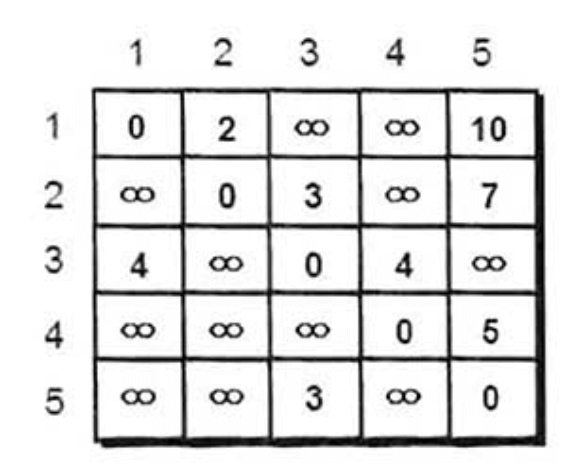
从1号城市到5号城市的通路,一共有3条,分别是:
- 1->2->3->4->5:路径长度为14
- 1->2->5:路径长度为9
- 1->5:路径长度为10
深度优先遍历的代码实现见下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <stdio.h>
int min=99999999,book[101],n,e[101][101]; //我们这里假设99999999为正无穷
//cur是当前所在的城市编号,dis是当前已经走过的路程
void dfs(int cur,int dis)
{
int j;
//如果当前走过的路程已经大于之前找到的最短路径,则没有必要再往下尝试了,立即返回
if(dis>min) return;
if(cur==n) //判断是否到达了目标城市
{
if(dis<min) min=dis; //更新最小值
return;
}
for(j=1;j<=n;j++) //从1号城市到n号城市依次尝试
{
//判断当前城市cur到城市j是否有路,并判断城市j是否在已走过的路径中
if(e[cur][j]!=99999999 && book[j]==0)
{
book[j]=1; //标记城市j已经在路径中
dfs(j,dis+e[cur][j]); //从城市j再出发,继续寻找目标城市
book[j]=0; //之前一步探索完毕之后,取消对城市j的标记
}
}
return;
}
int main()
{
int i,j,m,a,b,c;
scanf("%d %d",&n,&m);
//初始化二维矩阵
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=99999999;
//读入城市之间的道路
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&a,&b,&c);
e[a][b]=c;
}
//从1号城市出发
book[1]=1; //标记1号城市已经在路径中
dfs(1,0); //1表示当前所在的城市编号,0表示当前已经走过的路程
printf("%d",min); //打印1号城市到5号城市的最短路径
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。
1
2
3
4
5
6
7
8
9
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
运行结果是:
1
9
图就是有$N$个顶点和$M$条边组成的集合。图分为有向图和无向图,如果给图的每条边规定一个方向,那么得到的图称为有向图,其边也称为有向边。在有向图中,与一个点相关联的边有出边和入边之分,而与一个有向边关联的两个点也有始点和终点之分。相反,边没有方向的图称为无向图。
3.最少转机——图的广度优先遍历
1
2
3
4
5
6
7
8
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
第一行的5表示有5个城市(城市编号为1~5),7表示有7条航线,1表示起点城市,5表示目标城市。接下来7行每行是一条类似“a b”这样的数据表示城市a和城市b之间有航线,也就是说城市a和城市b之间可以相互到达。
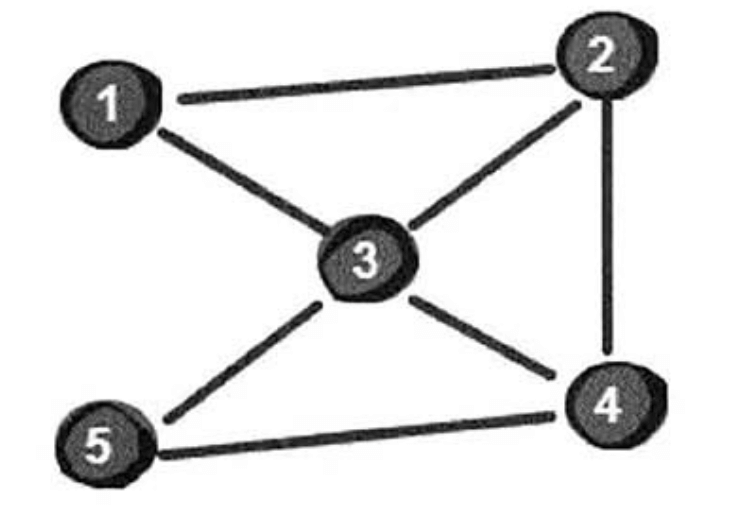
要求转机次数最少,所以我们可以认为所有边的长度都是1。使用广度优先搜索解决这个问题的代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <stdio.h>
struct note
{
int x; //城市编号
int s; //转机次数
};
int main()
{
struct note que[2501];
int e[51][51]={0},book[51]={0};
int head,tail;
int i,j,n,m,a,b,cur,start,end,flag=0;
scanf("%d %d %d %d",&n,&m,&start,&end);
//初始化二维矩阵
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=99999999;
//读入城市之间的航班
for(i=1;i<=m;i++)
{
scanf("%d %d",&a,&b);
//注意这里是无向图
e[a][b]=1;
e[b][a]=1;
}
//队列初始化
head=1;
tail=1;
//从start号城市出发,将start号城市加入队列
que[tail].x=start;
que[tail].s=0;
tail++;
book[start]=1; //标记start号城市已在队列中
//当队列不为空的时候循环
while(head<tail)
{
cur=que[head].x; //当前队列中首城市的编号
for(j=1;j<=n;j++) //从1~n依次尝试
{
//从城市cur到城市j是否有航班并且判断城市j是否已经在队列中
if(e[cur][j]!=99999999 && book[j]==0)
{
//如果从城市cur到城市j有航班并且城市j不在队列中,则将j号城市入队
que[tail].x=j;
que[tail].s=que[head].s+1; //转机次数+1
tail++;
//标记城市j已经在队列中
book[j]=1;
}
//如果到达目标城市,停止扩展,任务结束,退出循环
if(que[tail].x==end)
{
//注意下面两句话的位置千万不要写颠倒了
flag=1;
break;
}
}
if(flag==1)
break;
head++; //注意这地方,千万不要忘记当一个点扩展结束后,head++才能继续扩展
}
//打印队列中末尾最后一个(目标城市)的转机次数
//注意tail是指向队列队尾(即最后一位)的下一个位置,所以这需要-1
printf("%d",que[tail-1].s);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。
1
2
3
4
5
6
7
8
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
运行结果是:
1
2
当然也可以使用深度优先搜索解决,但是这里用广度优先搜索会更快。广度优先搜索更加适用于所有边的权值相同的情况。