本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.使用SVD压缩图片
👉读取图片:
1
2
from PIL import Image
img = Image.open("jojo.jpg")

👉转为数学矩阵:
1
2
3
4
5
6
import numpy as np
imgary = np.array(img)
imgary = imgary / 255
original_bytes = imgary.nbytes
print(original_bytes) #49766400
print(imgary.shape) #(1080, 1920, 3)
imgary在除以255之后,里面的元素类型是64位浮点数,即8字节,所以这张图像占用的内存大小为:$1080 \times 1920 \times 3 \times 8 = 49766400$。
👉拆分为RGB三色矩阵:
1
2
3
4
5
6
img_red = imgary[:,:,0]
img_green = imgary[:,:,1]
img_blue = imgary[:,:,2]
print(img_red.shape) #(1080, 1920)
print(img_green.shape) #(1080, 1920)
print(img_blue.shape) #(1080, 1920)
👉使用SVD分解矩阵:
1
2
3
4
from numpy.linalg import svd
U_r, S_r, V_r = svd(img_red, full_matrices=True)
U_g, S_g, V_g = svd(img_green, full_matrices=True)
U_b, S_b, V_b = svd(img_blue, full_matrices=True)
👉取用50个特征值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
k = 50
U_r_k = U_r[:, 0:k]
V_r_k = V_r[0:k, :]
U_g_k = U_g[:, 0:k]
V_g_k = V_g[0:k, :]
U_b_k = U_b[:, 0:k]
V_b_k = V_b[0:k, :]
S_r_k = S_r[0:k]
S_g_k = S_g[0:k]
S_b_k = S_b[0:k]
print(U_r_k.shape) #(1080, 50)
print(S_r_k.shape) #(50,)
print(V_r_k.shape) #(50, 1920)
👉计算压缩比:
1
2
3
compressed_bytes = sum([matrix.nbytes for matrix in [U_r_k,V_r_k,U_g_k,V_g_k,U_b_k,V_b_k,S_r_k,S_g_k,S_b_k]])
ratio = compressed_bytes / original_bytes
print(ratio) #0.07236207561728394
👉还原矩阵:
1
2
3
4
5
6
7
8
image_red_approx = np.dot(U_r_k, np.dot(np.diag(S_r_k), V_r_k))
image_green_approx = np.dot(U_g_k, np.dot(np.diag(S_g_k), V_g_k))
image_blue_approx = np.dot(U_b_k, np.dot(np.diag(S_b_k), V_b_k))
row, col, _ = imgary.shape
img_reconstructed = np.zeros((row, col, 3))
img_reconstructed[:, :, 0] = image_red_approx
img_reconstructed[:, :, 1] = image_green_approx
img_reconstructed[:, :, 2] = image_blue_approx
👉正规化异常值:
1
2
3
img_reconstructed[img_reconstructed < 0] = 0
img_reconstructed[img_reconstructed > 1] = 1
print(img_reconstructed.shape) #(1080, 1920, 3)
👉绘制还原图片:
1
2
3
4
fig = plt.figure(figsize=(10,5))
a = fig.add_subplot(1,1,1)
imgplot = plt.imshow(img_reconstructed)
plt.show()
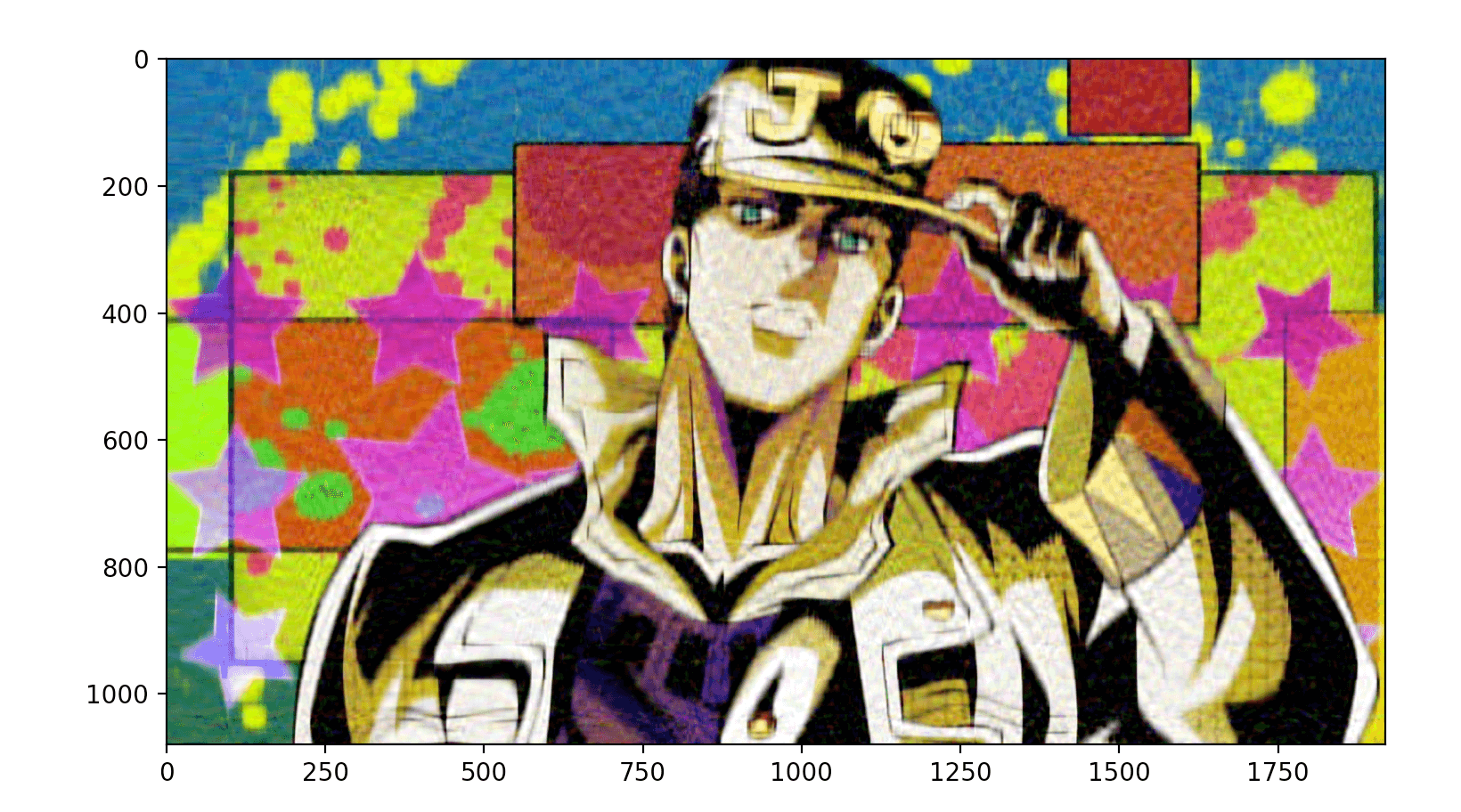
可见,SVD压缩图片属于有损压缩。