本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
在图像中检测人类是一项具有挑战性的任务,因为人物的外表和姿势都是多样化的。首先需要的是一个强大的特征集,即使在杂乱的背景下,也能清晰地区分人形。我们主要研究了用于人类检测的特征集,并提出了具有优异性能的HOG(Histogram of Oriented Gradient) descriptor。我们以“行人检测”作为测试案例,比较了不同detector的性能差异。为了简单和快速,我们在整个研究中使用线性SVM作为baseline分类器。新的detector在MIT行人测试集上取得了近乎完美的结果,因此我们创建了一个更具挑战性的测试集,包含1800多张具有各种姿势和背景的行人图像。并且我们的工作表明,我们的特征集在其他基于形状的目标检测任务中表现同样出色。
我们在文章第2部分介绍了人类检测领域之前的一些相关工作,在第3部分介绍了我们提出的方法,在第4部分介绍了我们的数据集,在第5-6部分给出了详细的描述和实验评估结果。在第7部分对主要结论进行总结。
2.Previous Work
有大量关于目标检测的文献,但这里我们只提到一些关于人类检测的相关论文。和之前的一些方法相比,我们的detector结构更加简单,在行人图像上的性能也更好。
3.Overview of the Method
本部分概述了我们提取特征的流程,如Fig1所示。实现细节会在第6部分详述。该方法基于在密集网格(dense grid)中评估图像梯度方向(经过良好归一化)的局部直方图。类似的特征在过去十年间被越来越多的使用。其基本思想就是局部目标的表征和形状可以很好的被梯度或边缘方向的分布所描述。在实现时,我们将图像划分为多个cell,在每个cell中,通过统计每个像素的梯度方向或边缘方向而得到一个一维的直方图。

如上图所示,绿色网格为划分的cell,在每个cell内计算每个像素的梯度幅值以及方向。如上图中间所示,蓝色箭头为梯度,箭头方向即为梯度方向,箭头长度即为梯度幅值。一个cell内所有像素的梯度统计结果见上图右。注意方向的范围在0到180度之间,而不是0到360度,这被称为“无符号”梯度,因为两个完全相反的方向被认为是相同的。
现在来计算一个cell的梯度直方图,假设将梯度方向范围分为9份,即直方图有9个bin,每20度为一个bin。
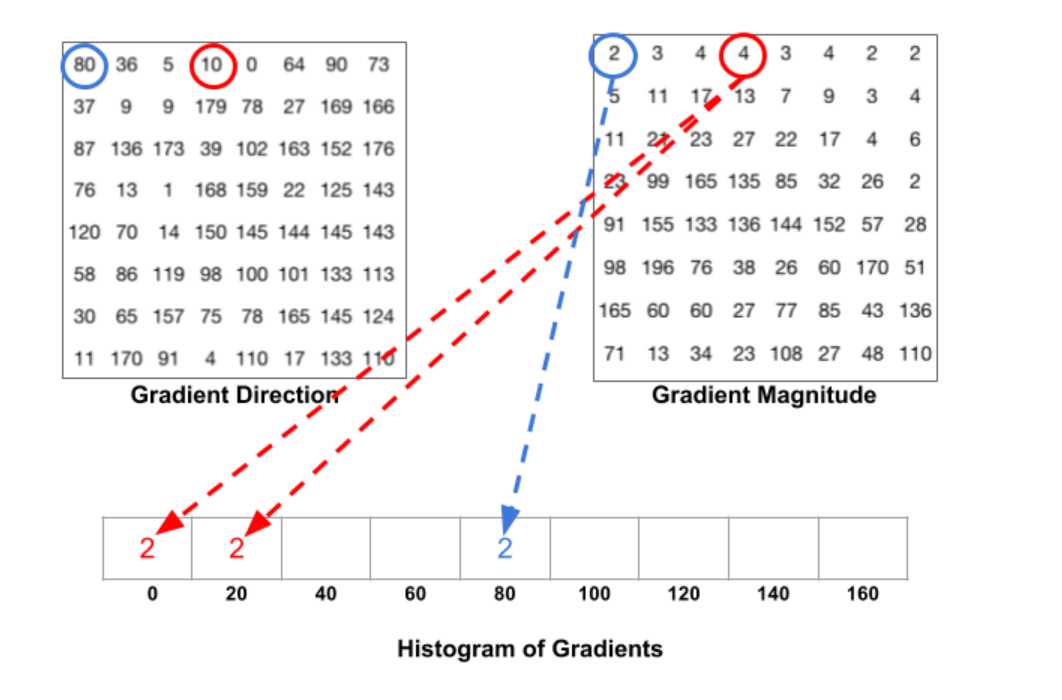
蓝圈像素的角度为80度,幅值为2,刚好可以把幅值2放在80对应的bin中。红圈像素的角度为10度,在0和20的正中间,所以其对应的幅值4按比例应该平均放在0和20对应的bin中,即各放入2即可。如果有像素的角度在160到180之间,则其对应的幅值就按比例分给0和160对应的bin。另外一个例子:
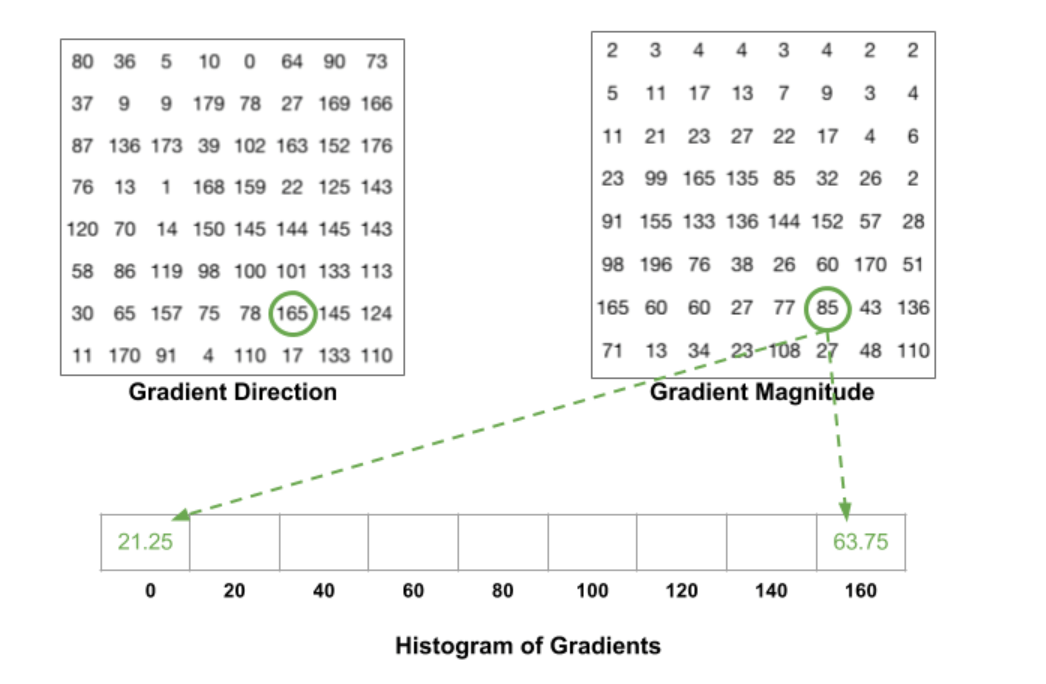
最终对于一个cell,就可以得到如下一个一维的直方图:
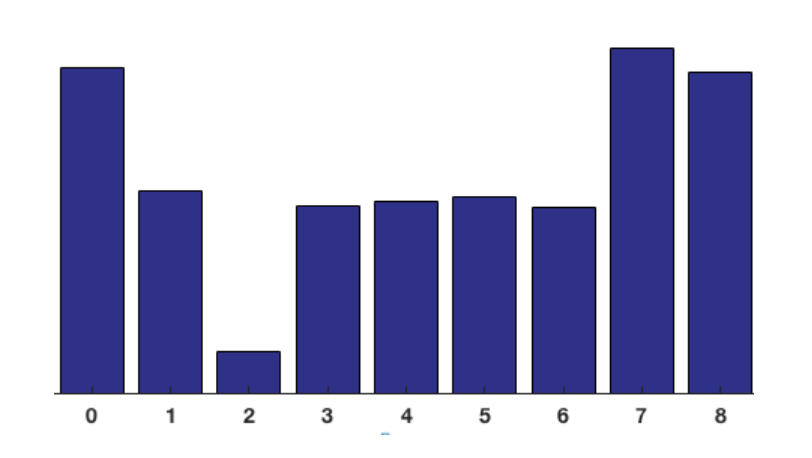
为了更好地增加对光照变化和阴影的鲁棒性,我们还进行了归一化操作。归一化是基于block进行的。

假设$2\times 2$个cell组成一个block,并使其在图像上进行滑动。那么一个block对应的特征向量的长度就是$4 \times 9 = 36$(一个block包含4个cell,每个cell可提取出一个长度为9的特征向量)。基于这36个值进行归一化操作。
我们将归一化后的block的特征向量称为HOG descriptors。将所有block求得的特征向量拼接起来就可以得到整幅图像的HOG descriptors,然后将其喂入线性SVM分类器(如Fig1所示)。
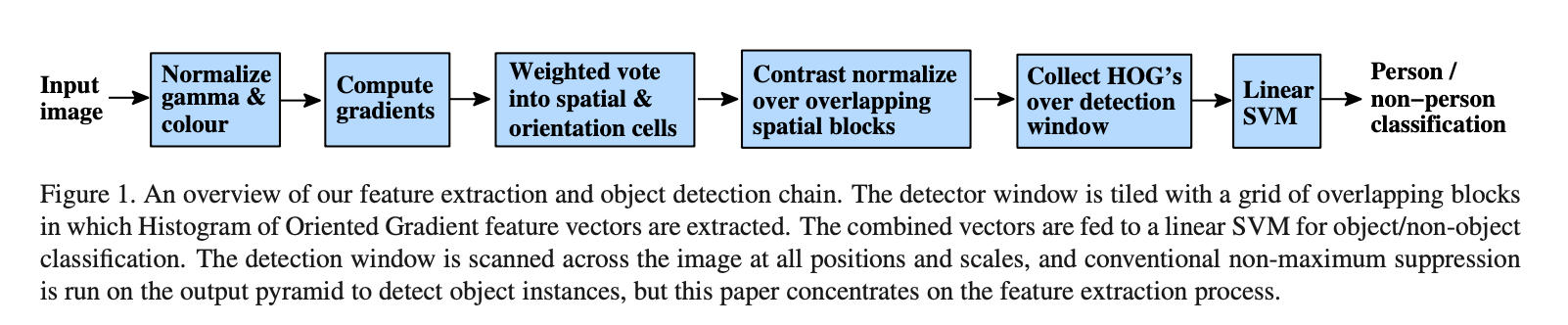
在之前的一些研究中,方向直方图就得到了使用,但直到SIFT出现,方向直方图的使用才达到成熟。此后,基于SIFT的一些方法在这种任务中表现的都非常好。但这些基于稀疏特征的方法的成功在一定程度上掩盖了基于密集特征的HOG方法的强大性和简单性。我们希望我们的研究可以纠正这一观点。此外,我们的非正式实验表明,即使是目前最好的基于关键点的方法,其假阳性率也可能比我们的密集网格方法高出至少1-2个数量级,这主要是因为我们所知道的关键点检测器都无法可靠地检测人体结构。
HOG/SIFT有一些共同的优点。它们能够捕获局部形状的边缘或梯度结构,从而易于在局部控制几何和光照不变性:因为在局部空间内或者在一个bin size内,平移和旋转所带来的变化会小得多。对于人类检测,粗糙的空间采样+精细的方向采样+局部光照归一化被证明是最好的策略,大概是因为它允许四肢和身体部分改变外观,以及在保持直立的情况下从一侧移动到另一侧。
4.Data Sets and Methodology
👉Datasets.
我们在两个不同的数据集上测试了我们的detector。第一个是MIT行人数据集,包含509张训练图像和200张测试图像(再额外加上图像的左右翻转)。但它只包含人物姿势的正面或反面图像。我们最好的detector在这个数据集上取得了近乎完美的结果,因此我们构建了一个新的,更具挑战性的数据集:“INRIA”,其包含从一组不同人照片中截取得到的1805张人类图像,这些图像的大小为$64 \times 128$。Fig2展示了一些例子。人物通常都是站立姿势,但会以任意方向出现,背景图像包括人群。背景中人物的姿势没有特殊的限制和要求。数据集可在http://lear.inrialpes.fr/data获得,可用于研究目的。

Fig2:我们新的人类检测数据库中的一些样本图像。目标总是直立的,但可能会有一些局部遮挡,姿势、外表、服装、照明和背景的变化很大。
👉Methodology.
训练所用的正样本一共有1239张图像,加上左右翻转,共计2478张图像。从1218张没有人的图像中采样得到12180个patch,作为初始负样本集。对于每个detector和参数的组合,我们都训练一个初步的detector,在1218张负样本图像上遍历预测,得到其预测错误的patch(即假阳,这些patch被称为“hard examples”)。然后将这个detector在初始的12180个patch+“hard examples”的组合数据集上重新进行训练,得到最终的detector。如果必要,可以对“hard examples”进行二次采样。重新训练明显提升了每个detector的性能(对于我们默认的detector,当FPPW$=10^{-4}$时,性能优化了5%,FPPW为False Positives Per Window的缩写),但增加再多的重新训练轮数就没什么用了。
为了量化detector的性能,我们在log-log scale上绘制了DET(Detection Error Tradeoff)曲线,即miss rate vs. FPPW,其中miss rate就是$1-Recall$或$\frac{FalseNeg}{TruePos+FalseNeg}$。值越低越好。
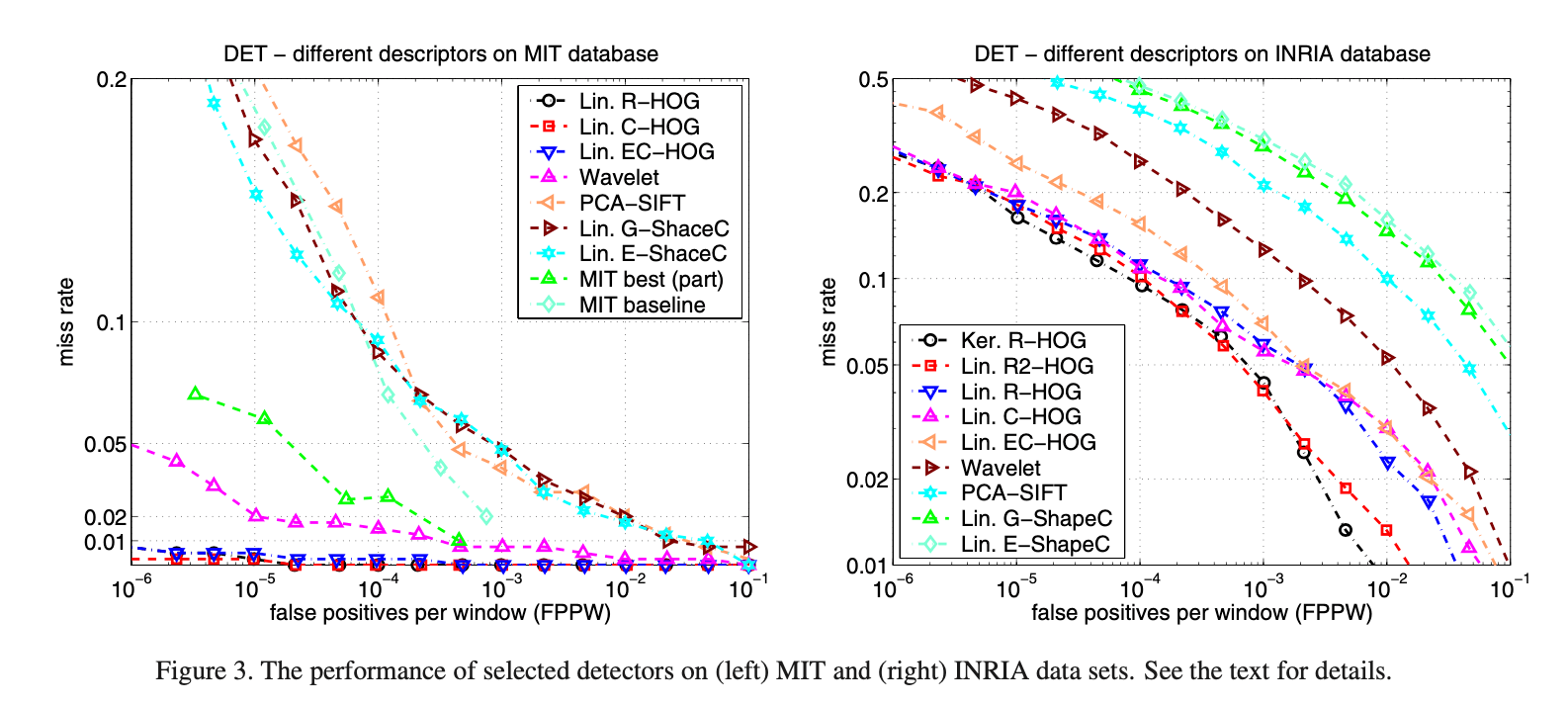
用Fig3解释下DET曲线,横轴是FPPW,即假阳的个数除以窗口数,用其对数形式表示。越靠左,FPPW数值越小,代表性能越好。纵轴是miss rate,即漏检率,miss rate计算公式中的分母$TruePos+FalseNeg$是真实阳性样本的总数量,是不变的,分子$FalseNeg$是没检测出的阳性样本的数量,漏检率当然是越低越好。类似ROC曲线,通过取不同的阈值(用于判定是否为阳性样本),可以得到一条DET曲线。那么两条DET曲线该怎么比较呢?比如,类似ROC,可以用曲线下面积,即AUC进行比较。而作者比较两条DET曲线,是比较其在FPPW$=10^{-4}$处的miss rate。
DET图被广泛应用于语音和NIST评估。在一个多尺度detector中,$10^{-4}$的FPPW相当于每测试一张$640 \times 480$大小的图像,就有约0.8个假阳的原始错误率。由于非极大值抑制,full detector的假阳性率更低。我们的DET曲线通常都很浅,即使在漏检率上仅有微小的改进,其相当于FPPW在恒定漏检率下的很大改进。举个例子,我们的默认detector,在FPPW为$1e-4$时,漏检率每降低1%的绝对值(9%的相对值),就相当于在恒定漏检率下,FPPW减少1.57倍。
5.Overview of Results
在介绍详细实现和性能分析之前,我们将最终的HOG检测器的总体性能与其他一些现有方法的性能进行了比较。将基于矩形(rectangular)block的R-HOG或基于圆形(circular log-polar)block的C-HOG,并搭配linear或kernel的SVM,和其他的一些比如Haar wavelet、PCA-SIFT、shape context等方法进行了比较。详细见下:
👉Results.
Fig3展示了MIT和INRIA数据集上各种detector的性能。基于HOG的detector明显优于wavelet、PCA-SIFT、shape context等detector,其在MIT数据集上的表现近乎完美,在INRIA数据集上FPPW至少低了一个数量级。R-HOG和C-HOG的性能非常接近。将R-HOG加上对二阶导数的统计,得到R2-HOG,特征向量的长度会翻倍,但进一步提高了性能(FPPW为$10^{-4}$时性能提升了2%)。如果我们将使用线性核的linear SVM换成使用高斯核的SVM,虽然运行时间增加,但在$10^{-4}$的FPPW下性能提升了约3%。我们使用linear R-HOG生成的“hard examples”来训练高斯核的R-HOG(kernel R-HOG),这是因为kernel R-HOG产生的假阳太少了,以至于无法显著提高其泛化能力。使用binary edge voting的EC-HOG比使用gradient magnitude weighted voting的C-HOG的性能低5%(FPPW为$10^{-4}$时),而忽略方向信息则会使性能降低更多。PCA-SIFT的表现也不好。
6.Implementation and Performance Study
我们现在给出HOG实现的细节,并系统地研究了各种选择对detector性能的影响。我们定义的默认detector有如下属性:没有使用gamma correction的RGB colour space;$[-1,0,1]$的梯度filter且没有使用平滑;对$0^\circ - 180^\circ$分成的9个bin进行linear gradient voting;一个cell是$8\times 8$个像素,一个block是$16\times 16$个像素;Gaussian spatial window的$\sigma$为8个像素;block归一化的方式为L2-Hys(Lowe-style clipped L2 norm);block的步长为8个像素(也就是说一个cell会被4个block所覆盖);检测窗口大小为$64 \times 128$;线性SVM分类器。
Fig4总结了各种HOG参数对整体检测性能的影响。主要结论是,为了获得良好的性能,应该使用精细尺度的导数(基本上没有平滑),较多的orientation bins以及适当大小、强归一化、有重叠的blocks。

Fig4中,(a)使用精细的导数尺度可以明显的提升性能(“c-cor”指的是cubic-corrected mask)。(b)在$0^\circ - 180^\circ$范围内,增加orientation bin的数量可显著提升性能,最多可增加至9个bin。(c)不同block归一化方法的效果。(d)使用有重叠的block可将miss rate降低约5%。(e)将$64\times 128$的检测窗口缩小会导致性能下降约4%。(f)使用Gaussian kernel SVM($-\gamma \parallel \mathbf{x}_1 - \mathbf{x}_2 \parallel ^2$),将性能提升了约3%。
6.1.Gamma/Colour Normalization
gamma correction可调节图像对比度,减少光照对图像的影响(包括光照不均和局部阴影),使过曝或欠曝的图像恢复正常,更接近人眼看到的图像。gamma correction公式:$f(x)=x^{\gamma}$,即输出图像是输入图像的幂函数,指数为$\gamma$。
我们评估了几种不同的颜色空间:灰度、RGB和LAB,并选择性的搭配gamma correction。RGB和LAB的结果差不多,灰度则会导致FPPW为$10^{-4}$时性能下降1.5%。将gamma correction应用于每个颜色通道,当$\gamma=0.5$时(即square root gamma compression),FPPW为$10^{-4}$时性能提升了1%,但如果使用log compression这种更强的压缩,则会导致FPPW为$10^{-4}$时性能反而下降2%。
6.2.Gradient Computation
detector的性能对梯度的计算方式很敏感,但反而最简单的方法是最好的。我们测试了使用高斯平滑后接一个离散的mask来计算导数。我们测试了多个平滑尺度,其中包括$\sigma = 0$(即没有平滑)。离散的mask就是导数的计算方式,测试了以下几种导数计算方式:
- 1-D point derivatives:
- uncentred:$[-1,1]$
- centred:$[-1,0,1]$
- cubic-corrected:$[1,-8,0,8,-1]$
- $3 \times 3$ Sobel masks
- $2 \times 2$ diagonal masks(最紧凑的2D导数mask):
- $\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$
- $\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}$
最简单的$[-1,0,1]$搭配$\sigma=0$得到的结果最好。更大的mask会降低性能,并且平滑也会严重损害性能:对于高斯平滑,当FPPW为$10^{-4}$时,当$\sigma$从0变到2时,recall rate从89%降到了80%。当$\sigma = 0$时,与使用$[-1,0,1]$相比,如果使用cubic-corrected mask,$10^{-4}$ FPPW的性能降低1%,如果使用$2\times 2$ diagonal masks,性能降低1.5%。同样,使用centred的$[-1,1]$ mask也会导致1.5%的性能下降(FPPW=$10^{-4}$)。
对于彩色图像,我们为每个颜色通道单独计算梯度,并将具有最大范数的通道作为该像素点的梯度向量(个人理解就是取多个通道中长度最大的梯度向量作为像素点的梯度向量)。
6.3.Spatial / Orientation Binning
cell的形状可以是矩形,也可以是radial(log-polar sectors,即对数极坐标,一个像素点被表示为一个对数距离和一个极角)。orientation bins的范围可以是$0^\circ - 180^\circ$(无符号梯度)或$0^\circ - 360^\circ$(有符号梯度)。统计的对象可以是梯度幅值或者是幅值的平方或平方根,又或者是其他一些形式。但通过实践,梯度幅值可以得到最好的结果。
如Fig4(b)所示,增加orientation bin的数量显著提升了性能,最多可到9个bin,再多作用就不明显了。这适用于$0^\circ - 180^\circ$的无符号梯度。如果像SIFT一样,使用$0^\circ - 360^\circ$的有符号梯度,则会导致性能下降,即使增加bin的数量也无济于事。对于人物来说,衣服和背景颜色的广泛性可能会使“符号”变得没有意义。但对于其他类型的目标识别任务(比如汽车、摩托车)等,“符号”信息会有很大的帮助。
6.4.Normalization and Descriptor Blocks
由于照明和前景/背景对比度的局部变化,导致梯度强度的变化很大,因此有效的局部对比度归一化对良好的性能至关重要。我们评估了多种不同的归一化方案。大多数方案都需要分成多个block,并分别对每个block进行归一化。最终的descriptor是窗口内所有block归一化特征向量的组合。实际上,block之间会有重叠。良好的归一化是至关重要的,并且重叠也可以显著提升性能。Fig4(d)展示了当block的移动步长从16(即没有重叠)变到4时,FPPW为$10^{-4}$时性能提升了4%。
我们评估了两种block形状,一种是矩形,对应的cell也是矩形,另一种是圆形,对应的cell用对数极坐标表示。我们分别将其称为R-HOG(rectangular HOG)和C-HOG(circular HOG)。
R-HOG.
R-HOG block和SIFT descriptors有很多相似之处,但它们的使用方式却截然不同。
Fig5展示了$10^{-4}$ FPPW下,在不同cell和block尺寸下,miss rate的值。对于人类检测,一个block为$3 \times 3$个cell,一个cell为$6 \times 6$个像素时,可以得到最佳性能,FPPW等于$10^{-4}$时的miss-rate为10.4%。我们所提出的标准模式,即一个block为$2 \times 2$个cell,一个cell为$8 \times 8$个像素,其性能排在第二。如果不考虑block的大小,通常一个cell的大小为6-8个像素时表现最好,巧合的是,在我们的图像中,人类的四肢大约刚好有6-8个像素。block的大小为$2 \times 2$或$3 \times 3$时,效果最好。如果block太大,则对局部图像的适应性会减弱,而当block太小时,有价值的空间信息则会被抑制。

Fig5:当FPPW为$10^{-4}$时,cell、block大小和miss rate之间的关系。步长固定为block size的一半。
和SIFT操作一样,在统计梯度直方图之前,会对梯度幅值做一个高斯加权(Gaussian spatial window),以降低边缘附近像素点的权重。当高斯的$\sigma=0.5 * block\_width$且FPPW为$10^{-4}$时,性能大约提升了1%。
我们还尝试了同时使用多种不同的block,比如cell大小不同或block大小不同。当FPPW为$10^{-4}$时,性能提升了3%左右,但descriptor的size也急剧增加。
除了正方形的block,我们还尝试了vertical block($2\times 1$ cell)、horizontal block($1 \times 2$ cell)以及二者的组合。vertical block和vertical+horizontal block明显优于单独的horizontal block,但它们都比不上$2 \times 2$或$3 \times 3$的cell block(FPPW=$10^{-4}$时的性能低了1%)。
C-HOG.

如上图所示,关于C-HOG所用block和cell的几何形状,我们评估了两种,分别是上图中(即中间的cell被分成4个扇区)和上图右(即中间有一个完整的cell)。C-HOG的布局有4个参数:angular bin和radial bin的数量、central bin的半径(以像素为单位)、后续半径扩展系数。个人理解,radial bin就是同心圆的数量,如上图中或上图右所示,一个内圆,一个外圆,一共是2个radial bin,而angular bin就是角度分为几个区间,上图中和上图右都可以看作是分成4个角度区间,即有4个angular bin。如果要获得好的性能,至少需要两个radial bin(一个centre,一个surround)和四个angular bin(quartering,即每90度为一个区间)。增加更多的radial bin对性能不会产生太大的影响,但过多的angular bin会使性能降低(当angular bin的数量从4个增加到12个时,FPPW=$10^{-4}$处的性能降低了1.3%)。centre radial bin的最佳半径是4个像素,但3或5个像素也能得到接近的性能。扩展系数从2增加到3,性能基本保持不变。有了这些参数,无论是使用高斯空间加权还是按cell面积进行加权(指的是对梯度幅值的加权),性能都是一样的,但是如果把二者结合起来,则性能会略有降低。
Block Normalization schemes.
对每一种不同几何形状的HOG,我们都评估了4种不同的归一化方案。我们用$\mathbf{v}$表示未归一化的descriptor vector,$\parallel \mathbf{v} \parallel_k$是k-norm($k=1,2$),$\epsilon$是一个很小的常数。4种归一化方案分别为:
- L2-norm:$\mathbf{v} \to \mathbf{v} / \sqrt{\parallel \mathbf{v} \parallel ^2_2 + \epsilon^2}$。
- L2-Hys:先进行L2-norm,然后进行clipping(即将$\mathbf{v}$的最大值限制为0.2),最后再一次进行归一化。
- L1-norm:$\mathbf{v} \to \mathbf{v} / (\parallel \mathbf{v} \parallel_1 + \epsilon)$。
- L1-sqrt:$\mathbf{v} \to \sqrt{\mathbf{v} / (\parallel \mathbf{v} \parallel_1 + \epsilon)}$。
如Fig4(c)所示,L2-Hys、L2-norm和L1-sqrt的表现一样好,但简单的L1-norm却使性能下降了5%,而完全省略归一化则使性能降低了27%(均是在FPPW为$10^{-4}$时的性能测量)。
Centre-surround normalization.
“window norm”用于centre-surround风格的cell归一化。如Fig4(c)所示,其性能低于基于block的归一化方案。其中一个原因是这里没有重叠的block,每个cell在最终的descriptor中只被编码了一次。

Fig6:我们的HOG detector主要可以检测到人体轮廓(尤其是头部、肩部和脚部)。the most active blocks主要集中在轮廓外的背景图像上。(a)训练样本的平均梯度图像。(b)SVM为特征向量中的每个元素都学得了一个权重,该图就是像素在其所在block内最大正权重的表示。(c)和图b类似,这里是最小负权重的表示。(d)测试图像。(e)R-HOG descriptor的表示。按cell进行表示,每个cell分9个方向,每个方向上射线的长度即该方向上的投票结果。(f,g)是R-HOG descriptor经过SVM权重加权后的可视化。图f是正权重的结果,图g是负权重的结果。
6.5.Detector Window and Context
检测窗口的大小是$64 \times 128$,在人物四周大约留出了16个像素的buffer。从Fig4(e)可以看出,该窗口大小性能是最好的。如果我们将buffer从16个像素降为8个像素(即检测窗口大小变为$48 \times 112$),FPPW=$10^{-4}$时的性能降低4%。如果保持窗口大小为$64 \times 128$,但增加人物的占比,也就相当于变相缩减了buffer,也会导致类似的性能损失。

6.6.Classifier
默认情况下,我们使用$C=0.01$的soft linear SVM。使用Gaussian kernel SVM可将FPPW在$10^{-4}$处的性能提升约3%,但也需要更多的运行时间。
6.7.Discussion
总的来说,我们的工作有几个显著的发现。HOG的性能远远优于小波(wavelets),并且在计算梯度之前任何显著的平滑操作都会损害HOG的结果,这一事实说明许多可用的图像信息来自图像像素突变的边缘,而模糊这些信息以降低对空间位置的敏感度是一个错误。相反,梯度应该在最精细的尺度上进行计算,然后再进行平滑/模糊。
其次,强的局部归一化对良好的结果至关重要。在我们的标准detector中,每个HOG cell会出现在4个block中,即具有4次不同的归一化,这种操作可以将FPPW在$10^{-4}$处的性能从84%提升至89%。
7.Summary and Conclusions
对前文的总结,不再赘述。
Future work:
尽管我们目前的linear SVM detector相当高效——处理一张$320 \times 240$的图像(4000个检测窗口)不到一秒——但其仍有优化的空间。我们也还在继续研究基于HOG的detector,比如加入block matching或光流场。
8.原文链接
👽Histograms of Oriented Gradients for Human Detection