本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.LBP特征介绍
LBP(Local Binary Patterns,局部二值模式)是一种用来描述图像局部纹理特征的算子,LBP特征具有灰度不变性和旋转不变性等显著优点。它将图像中的各个像素与其邻域像素值进行比较,将结果保存为二进制数,并将得到的二进制比特串作为中心像素的编码值,也就是LBP特征值。LBP提供了一种衡量像素间邻域关系的特征模式,因此可以有效地提取图像的局部特征,而且由于其计算简单,可用于基于纹理分类的实时应用场景,例如目标检测、人脸识别等。
2.原始LBP特征
LBP特征的计算基于灰度图像,在图像中取一个$3 \times 3$的窗口,以窗口中心像素的灰度值作为阈值,将8邻域像素的灰度值与其进行比较,若邻域像素值大于阈值,则取1,否则取0。
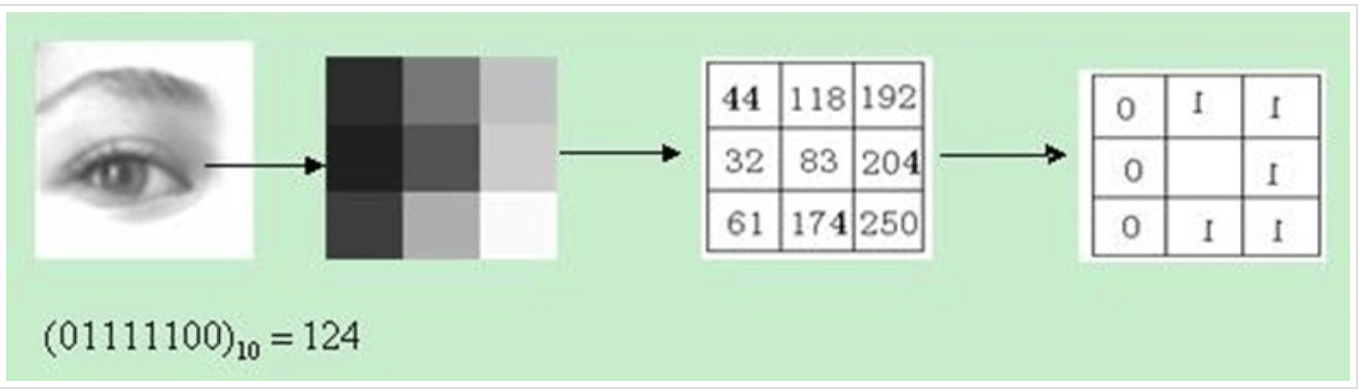
从窗口的左上角开始顺时针读取,便可得到01111100的8位二进制数,即所谓的LBP特征值。因为有8位二进制,所以LBP特征值有$2^8=256$个。此外,我们可以把01111100对应的十进制数124赋给中间像素,这样就可以将LBP特征以灰度图的形式表达出来。效果如下图所示:

3.圆形LBP特征
原始LBP特征考虑的是固定半径范围内的邻域像素,不能满足不同尺寸和频率纹理的需求,当图像的尺寸发生变化时,LBP特征将不能正确编码局部邻域的纹理信息。为了适应不同尺寸的纹理特征,对LBP算子进行改进,将$3\times 3$邻域窗口扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的LBP算子允许在半径为$R$的邻域内有任意多个像素点,从而得到在半径为$R$的区域内含有$P$个采样点的LBP算子。
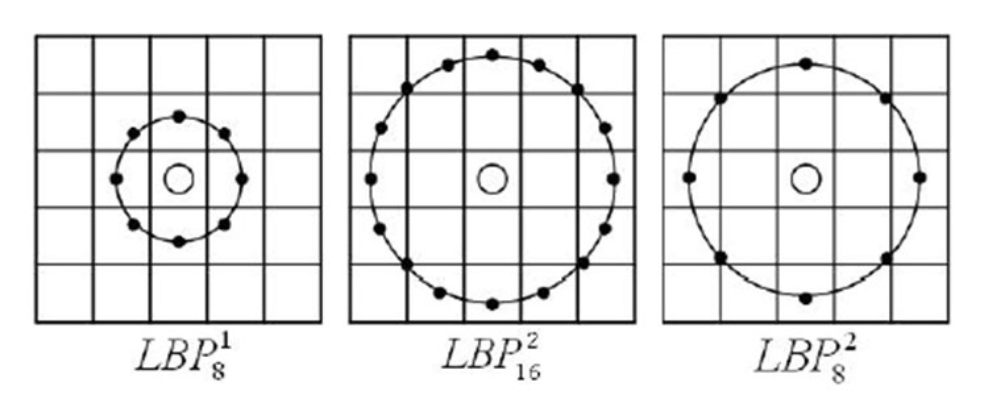
$LBP^R_P$如上图所示(采样点均匀分布在圆上)。采样点的坐标可通过以下公式计算:
\[x_p = x_c + R \cos (\frac{2\pi p}{P})\] \[y_p = y_c + R \sin (\frac{2\pi p}{P})\]其中$(x_c,y_c)$为中心像素点,$(x_p,y_p), p \in P$为邻域内某个采样点。采样点的坐标值未必是整数,可以通过插值来解决。效果如下图所示:

圆形LBP特征英文为“Circular LBP”或“Extended LBP”。
4.旋转不变LBP特征
无论是原始LBP算子还是圆形LBP算子,都只是灰度不变的,而不是旋转不变的,旋转图像会得到不同的LBP特征值。于是又提出了一种具有旋转不变性的LBP算子,即不断旋转圆形邻域的采样点,或者以不同的邻域像素作为起始点,顺时针遍历所有采样点,得到一些列编码值($P$个),取其中最小的作为该邻域中心像素的LBP值。旋转不变LBP算子的示意图如下:
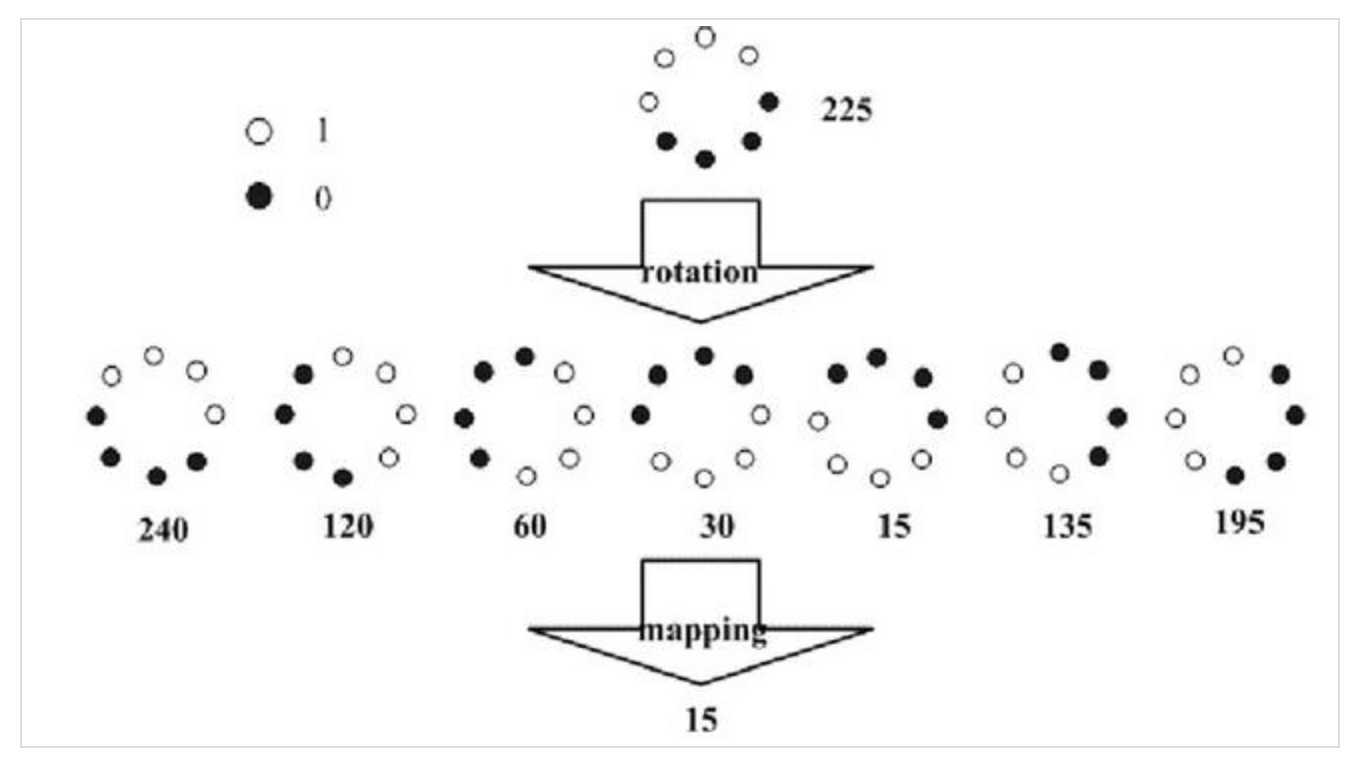
解释一下:
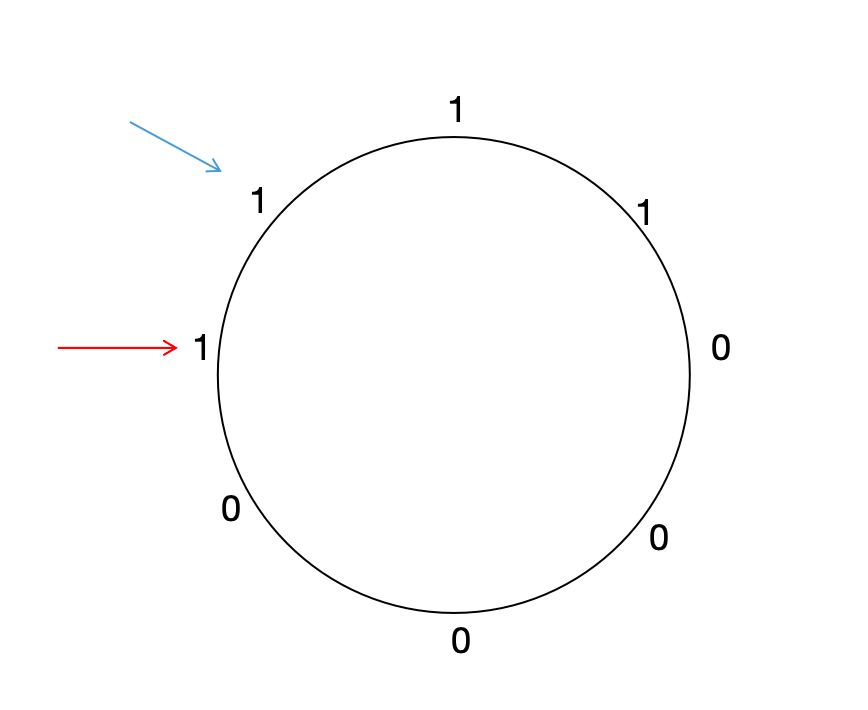
如果从蓝色箭头开始顺时针取值,我们可以得到11100001,对应十进制为225。而如果我们从红色箭头开始顺时针取值,我们可以得到11110000,对应十进制为240。
旋转不变LBP特征的英文为“Rotation Invariant LBP”。
5.LBP等价模式
对于一个半径为$R$的圆形区域,包含有$P$个邻域采样点,则LBP算子可能产生$2^P$种取值(或称为模式)。随着邻域内采样点数的增加,LBP值的取值数量呈指数级增长。例如,$5 \times 5$邻域内20个采样点,则会有$2^{20}$种取值,过多的二进制数不利于纹理信息的提取、分类、识别。例如,将LBP特征用于纹理分类或人脸识别时,一般采用LBP特征的统计直方图来表达图像的信息,而较多的二进制取值将使得数据量过大,且直方图过于稀疏。因此,需要对原始的LBP特征进行降维,使得数据量减少的情况下能最好地表达图像的信息。
为了解决二进制模式过多的问题,提高统计性,提出了一种“等价模式”(Uniform Pattern)来对LBP特征的模式种类进行降维。认为在实际图像中,绝大数LBP模式最多只包含两次从0到1或者从1到0的跳变。“等价模式”的定义为:当某个LBP所对应的循环二进制数从0到1或者从1到0最多有两次跳变时,该LBP所对应的二进制就是一个等价模式类,如00000000(0次跳变)、11000011(2次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共4次跳变)。通过改进,二进制模式的种类大大减少,由原来的$2^P$种降为$P(P-1)+2+1$种,其中$P(P-1)$为2次跳变的模式数,2为0次跳变(全“0”或全“1”)的模式数,1为混合模式的数量,由于是循环二进制数,因此“0”、“1”跳变次数不可能为奇数次。对于$3 \times 3$邻域内8个采样点来说,二进制模式由原始的256种变为59种。这使得特征向量的维度大大减少,并且可以减少高频噪声带来的影响。实验表明,一般情况下,等价模式的数目占全部模式的90%以上,可以有效对数据进行降维。下图为58种等价模式类:
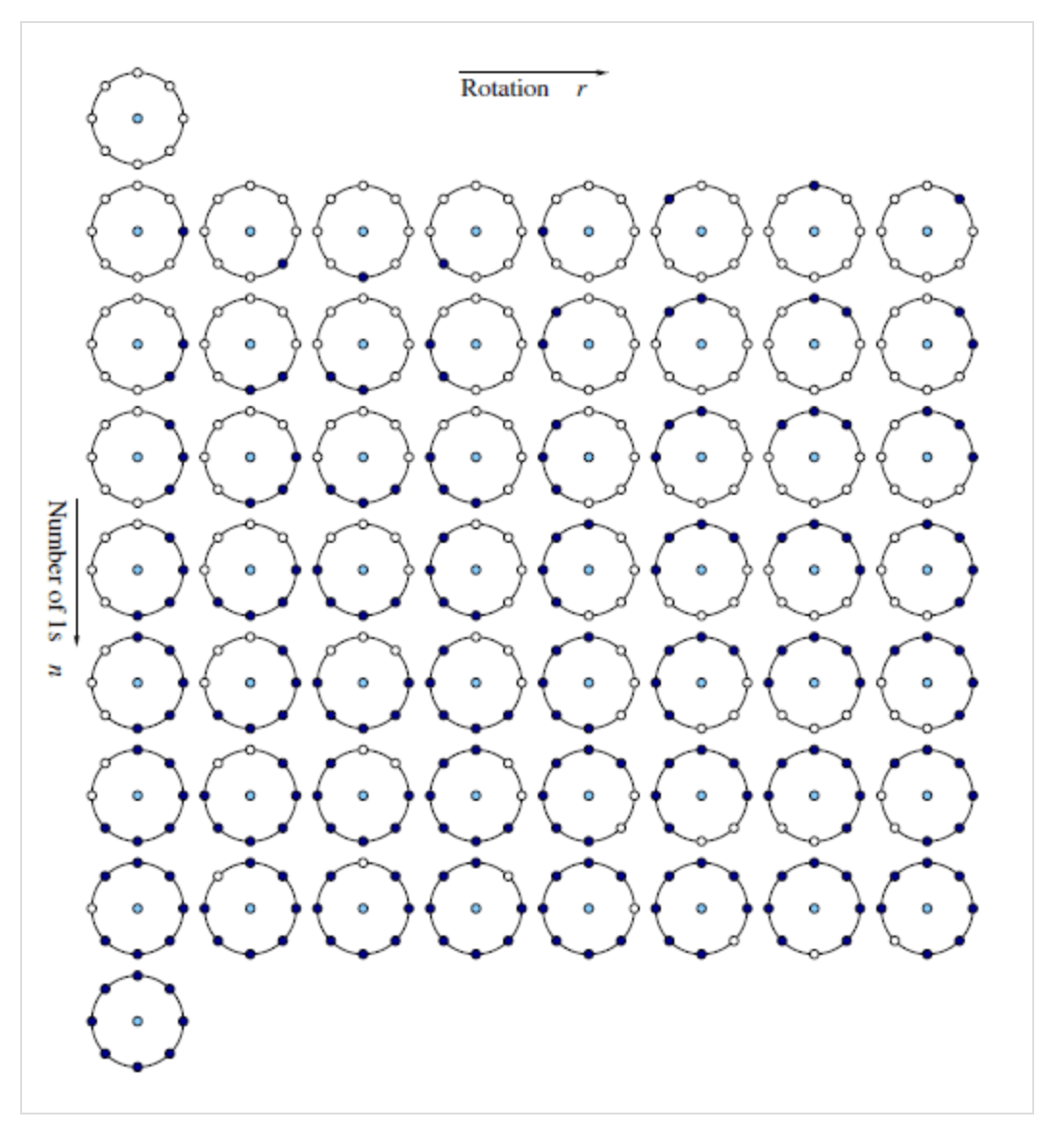
此外,旋转不变的Uniform LBP算子的等价模式类的数目为$P+1$个,对于8个采样点,基于等价模式的旋转不变LBP模式只有9个输出,该模式对于上图的Uniform LBP,每一行都是旋转不变的,对应同一个编码值。
6.多尺度LBP
基本LBP算子获取的是单个像素和其邻域像素间的纹理信息,属于微观特征。因此提出了一种多尺度LBP算子(Multiscale Block LBP,MB-LBP),将图像分为一个个的block,再将每个block分为一个个的cell,类似于HOG特征,cell内的灰度平均值或者和作为当前cell的灰度阈值,与邻域cell进行比较得到LBP值,生成的特征即为MB-LBP。block大小为$3\times 3$,cell大小为$1 \times 1$,就是原始的LBP特征。下图是一个大小为$9 \times 9$的block,cell大小为$3\times 3$:
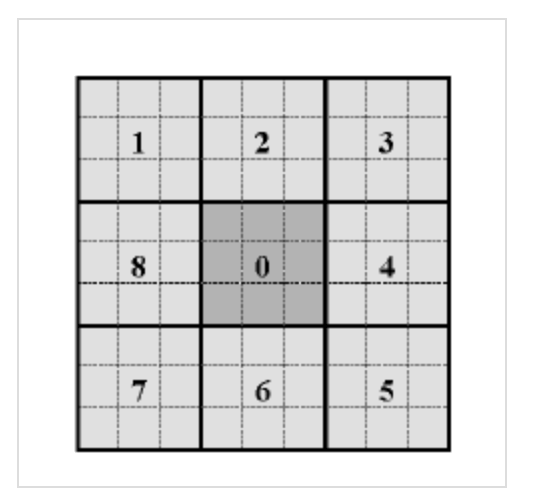
7.图像的LBP特征向量
对图像中的每个像素求取LBP特征值可得到图像的LBP特征图谱,但一般不直接将LBP图谱作为特征向量用于分类识别,而是类似于HOG特征,采用LBP特征的统计直方图作为特征向量。将LBP特征图谱划分为若干个子连通区域,并提取每个局部块的直方图,然后将这些直方图一次连接在一起形成LBP特征的统计直方图(Local Binary Patterns Histograms,LBPH),即可用于分类识别的LBP特征向量。
LBP特征向量的具体计算过程如下:
- 按照上述算法计算图像的LBP特征图谱。
- 将LBP特征图谱分块,例如分成$8 \times 8 = 64$个区域。
- 计算每个子区域中LBP特征值的统计直方图,并进行归一化,直方图大小为$1\times numPatterns$(numPatterns为模式数量)。
- 将所有区域的统计直方图按空间顺序依次连接,得到整幅图像的LBP特征向量,大小为$1\times numPatterns \times 64$。
- 从足够数量的样本中提取LBP特征,并利用机器学习的方法进行训练得到模型,用于分类和识别等领域。
对于LBP特征向量的维度,如果是原始的LBP特征,邻域采样点为8个,其模式数量为256,特征维数为$64 \times 256 = 16384$;如果是Uniform LBP特征,其模式数量为59,特征维数为$64 \times 59 = 3776$,使用等价模式特征,可以有效进行数据降维,而对模型性能却无较大影响。