博客为参考《啊哈!算法》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.镖局运镖——图的最小生成树
kruskal算法:kruskal算法。
2.再谈最小生成树
prim算法:prim算法。
3.重要城市——图的割点
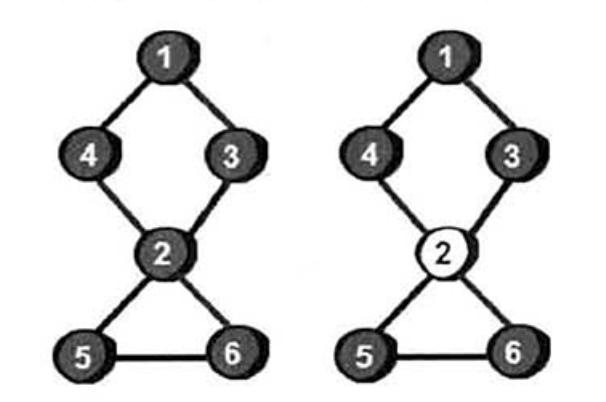
在上述无向连通图中,如果删除2号顶点后,图不再连通(即任意两点之间不能相互到达),我们称这样的顶点为割点(或者称割顶)。那么割点如何求呢?
很容易想到的方法是:依次删除每一个顶点,然后用深度优先搜索或者广度优先搜索来检查图是否依然连通。如果删除某个顶点后,导致图不再连通,那么刚才删除的顶点就是割点。这种方法的时间复杂度是O(N(N+M))。想一想有没有更好的方法呢?能找到线性的方法吗?
首先我们从图中的任意一个点(比如1号顶点)开始对图进行遍历,比如使用深度优先搜索进行遍历,下图就是一种遍历方案。从图中可以看出,对一个图进行深度优先遍历将会得到这个图的一个生成树(并不一定是最小生成树),如下图。有一点需要特别说明的是:下图中圆圈中的数字是顶点编号,圆圈右上角的数表示的是这个顶点在遍历时是第几个被访问到的,这还有个专有名词叫做“时间戳”。例如1号顶点的时间戳为1,2号顶点的时间戳为3$\cdots \cdots$我们可以用数组num来记录每一个顶点的时间戳。
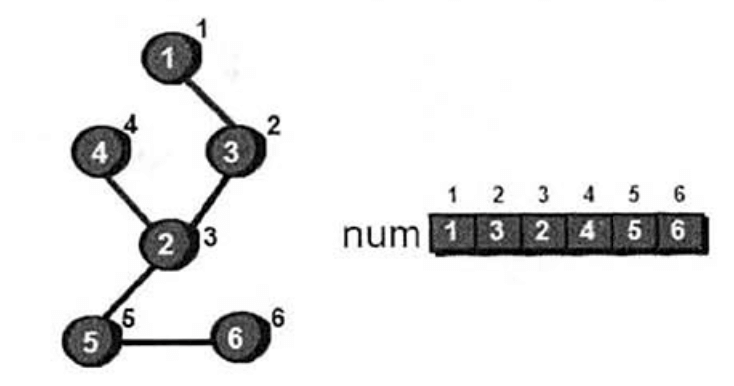
现在再来介绍另外一个概念:追溯值。追溯值指的是从当前顶点出发,通过一条非搜索树上的边,能够到达的时间戳最小的顶点。我们用数组low来保存每个顶点的追溯值。
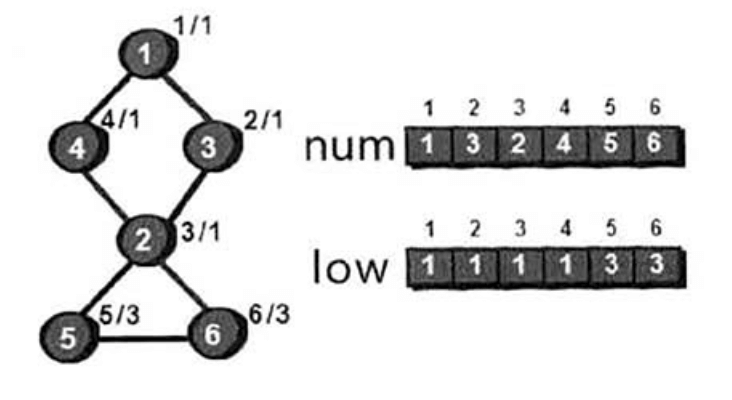
接下来详细说下数组low的计算。按照DFS的方法,从顶点1出发,顶点1的时间戳和追溯值设为$(1,1)$,其中第一个数为该顶点的时间戳,第二个数为该顶点的追溯值,初始追溯值和时间戳保持一致。
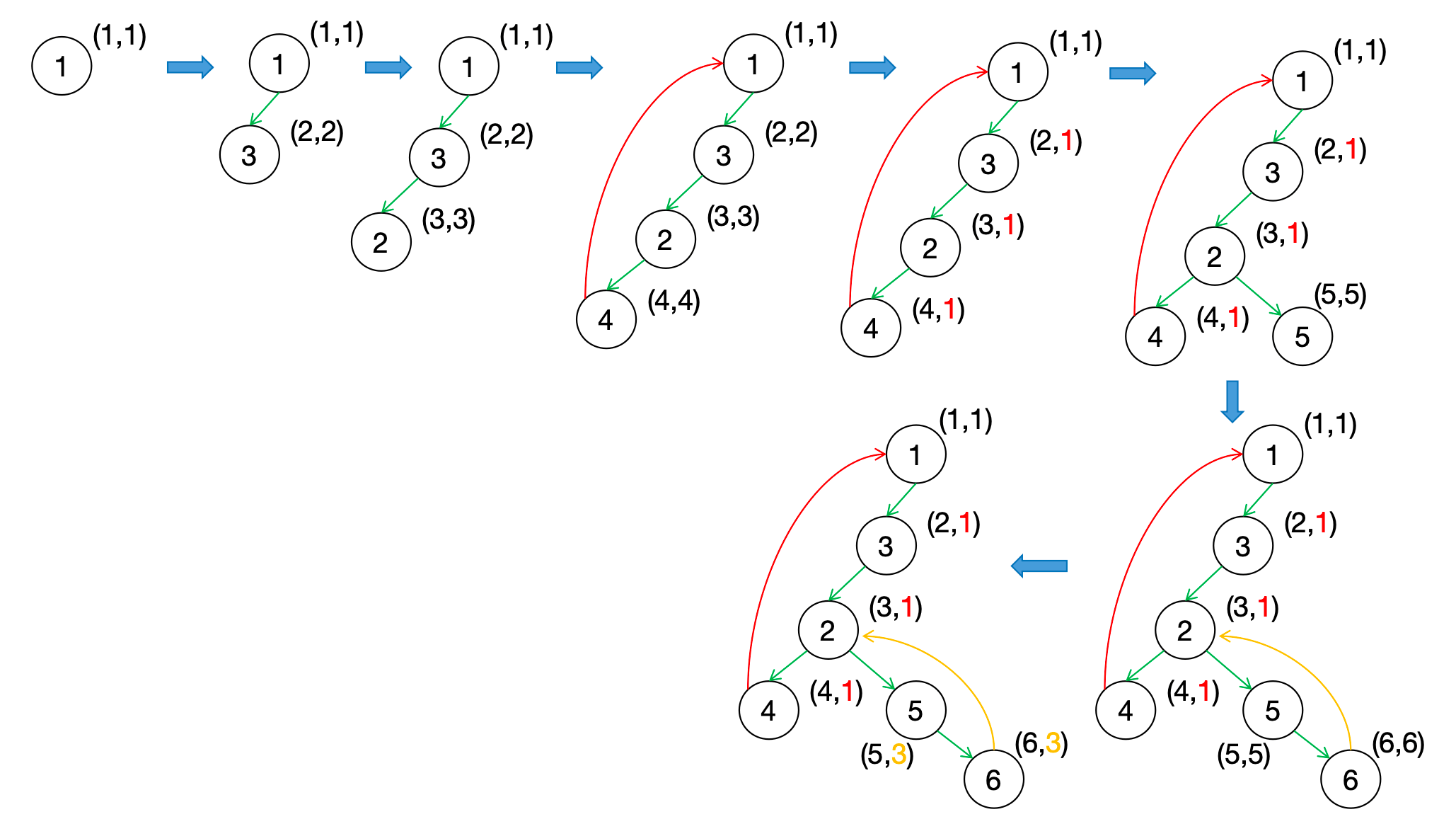
附上参考资料1中的动图例子更方便理解:
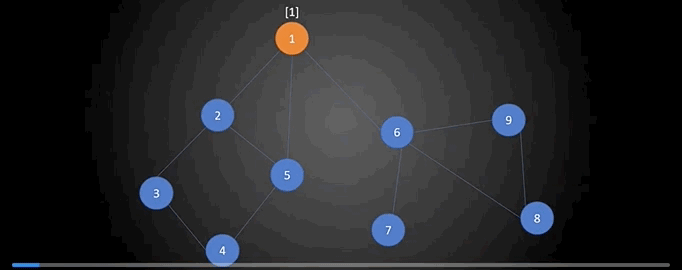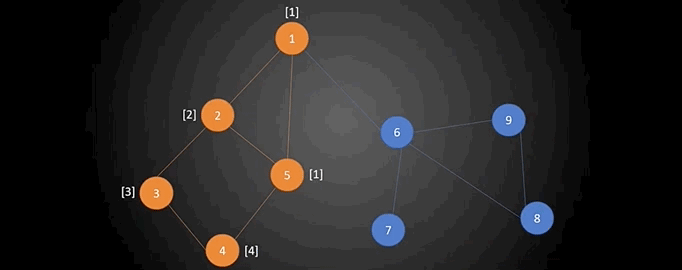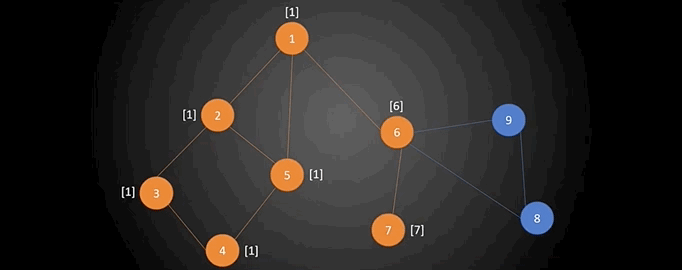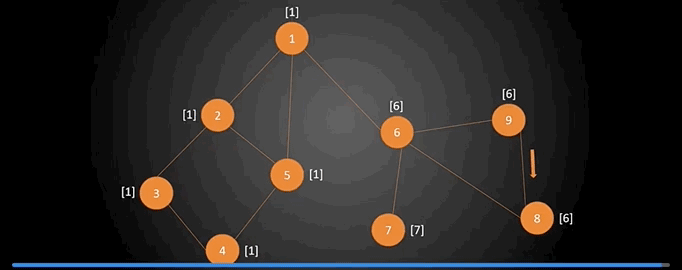
判定割点的两个条件:
- 如果顶点x不是根节点且有儿子,此时如有low[x的儿子]$\geqslant$num[x],那么x就是割点。
- 如果顶点x是根节点且有$\geqslant$2个儿子,那么x就是割点。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <stdio.h>
int n,m,e[9][9],root;
int num[9],low[9],flag[9],index;//index用来进行时间戳的递增
//求两个数中较小一个数的函数
int min(int a, int b)
{
return a < b ? a : b;
}
//割点算法的核心
void dfs(int cur, int father)//需要传入的两个参数,当前顶点编号和父顶点的编号
{
int child=0,i,j;//child用来记录在生成树中当前顶点cur的儿子个数
index++;//时间戳加1
num[cur]=index;//当前顶点cur的时间戳
low[cur]=index;//当前顶点cur能够访问到最早顶点的时间戳,刚开始当然是自己啦
for(i=1;i<=n;i++)//枚举与当前顶点cur有边相连的顶点i
{
if(e[cur][i]==1)
{
if(num[i]==0)//如果顶点i的时间戳不为0,说明顶点i还没有被访问过
{
child++;
dfs(i,cur);//继续往下深度优先遍历
//更新当前顶点cur能否访问到最早顶点的时间戳
low[cur]=min(low[cur],low[i]);
//如果当前顶点不是根节点并且满足low[i]>=num[cur],则当前顶点为割点
if(cur!=root && low[i]>=num[cur])
flag[cur]=1;
//如果当前顶点是根节点,在生成树中根节点必须要有两个儿子,那么这个根节点才是割点
if(cur==root && child==2)
flag[cur]=1;
}
else if(i!=father)//否则如果顶点i曾经被访问过,并且这个顶点不是当前顶点cur的父亲,则需要更新当前结点cur能否访问到最早顶点的时间戳
{
low[cur]=min(low[cur],num[i]);
}
}
}
}
int main()
{
int i,j,x,y;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
e[i][j]=0;
for(i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
e[x][y]=1;
e[y][x]=1;
}
root=1;
dfs(1,root);//从1号顶点开始进行深度优先遍历
for(i=1;i<=n;i++)
{
if(flag[i]==1)
printf("%d ",i);
}
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。第一行有两个数n和m,n表示有n个顶点,m表示有m条边。接下来m行,每行形如“a b”表示顶点a和顶点b之间有边。
1
2
3
4
5
6
7
8
6 7
1 4
1 3
4 2
3 2
2 5
2 6
5 6
运行结果是:
1
2
上面的代码是用的邻接矩阵来存储图,这显然是不对的,因为这样无论如何时间复杂度都会在$O(N^2)$,因为边的处理就需要$N^2$的时间。这里这样写是为了突出割点算法部分,实际应用中需要改为使用邻接表来存储,这样整个算法的时间复杂度是$O(N+M)$。
4.关键道路——图的割边
在一个无向连通图中,如果删除某条边后,图不再连通,则这条边称为割边(也称为桥)。下图中左图不存在割边,而右图有两条割边分别是2-5和5-6。
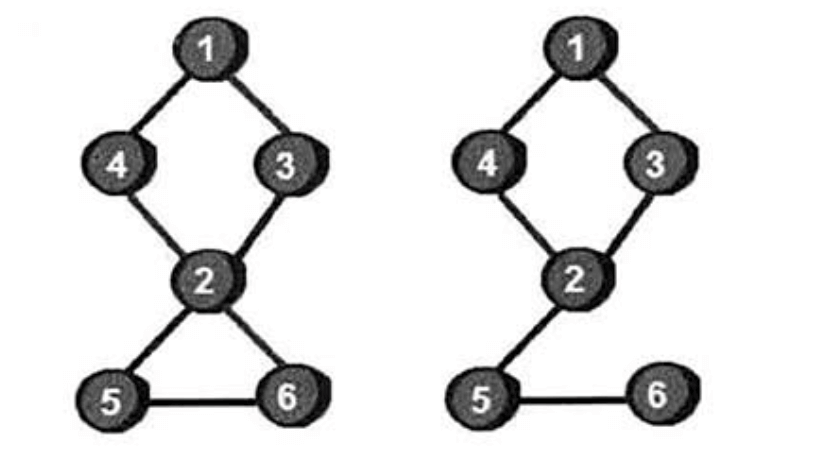
边$x\to y$是桥的判定条件为:low[y]>num[x]。代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>
int n,m,e[9][9],root;
int num[9],low[9],index;
int min(int a, int b)
{
return a < b ? a : b;
}
void dfs(int cur, int father)
{
int i,j;
index++;
num[cur]=index;
low[cur]=index;
for(i=1;i<=n;i++)
{
if(e[cur][i]==1)
{
if(num[i]==0)
{
dfs(i,cur);
low[cur]=min(low[i],low[cur]);
if(low[i]>num[cur])
printf("%d-%d\n",cur,i);
}
else if(i!=father)
{
low[cur]=min(low[cur],num[i]);
}
}
}
}
int main()
{
int i,j,x,y;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
e[i][j]=0;
for(i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
e[x][y]=1;
e[y][x]=1;
}
root=1;
dfs(1,root);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。第一行有两个数n和m。n表示有n个顶点,m表示有m条边。接下来m行,每行形如“a b”表示顶点a和顶点b之间有边。
1
2
3
4
5
6
7
6 6
1 4
1 3
4 2
3 2
2 5
5 6
运行结果是:
1
2
5-6
2-5
同割点的实现一样,这里也是用的邻接矩阵来存储图的,实际应用中需要改为使用邻接表来存储,否则这个算法就不是$O(N+M)$了,而至少是$O(N^2)$。
求割点和割边的算法称为tarjan算法。
5.我要做月老——二分图最大匹配
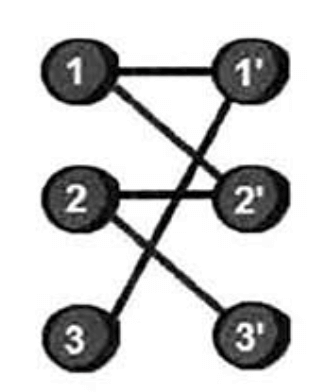
如上图,左边的顶点代表女生,右边的顶点代表男生。如果顶点之间有边,则表示他们可以坐在一起。像这样特殊的图叫做二分图(注意二分图是无向图)。二分图的定义是:如果一个图的所有顶点可以被分为X和Y两个集合,并且所有边的两个顶点恰好一个属于集合X,另一个属于集合Y,即每个集合内的顶点没有边相连,那么此图就是二分图。对于上面的例子,我们很容易找到两种分配方案,如下。
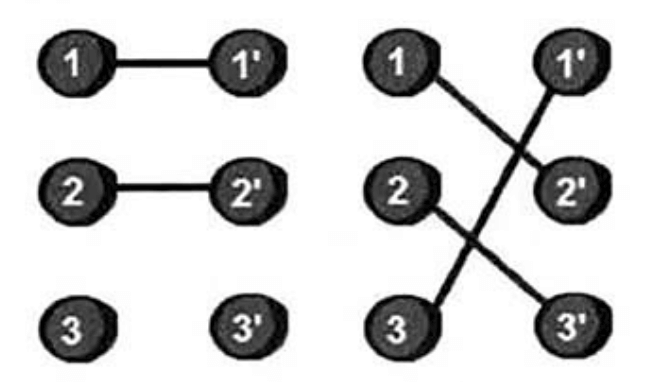
很显然右边的分配方案更好。我们把一种分配方案叫做一种匹配。那么现在的问题就演变成求二分图的最大匹配(配对数最多)。求最大匹配最容易想到的方法是:找出全部匹配,然后输出配对数最多的。这种方法的时间复杂度是非常高的,那还有没有更好的方法呢?
首先从左边的第1号女生开始考虑。先让她与1号男生配对,配对成功后,紧接着考虑2号女生。2号女生可以与2号男生配对,接下来继续考虑3号女生。此时我们发现3号女生只能和1号男生配对,可是1号男生已经配给1号女生了,怎么办?
于是1号男生让1号女生去尝试能否与其他认识的男生坐一起。然后,1号女生找到了2号男生,但2号男生已经和2号女生配对成功了,所以2号男生就让2号女生去尝试能否与其他认识的男生坐一起。接下来,2号女生找到了3号男生,刚好3号男生是空着的,于是,2号女生和3号男生配对成功,2号男生和1号女生配对,1号男生和3号女生配对。
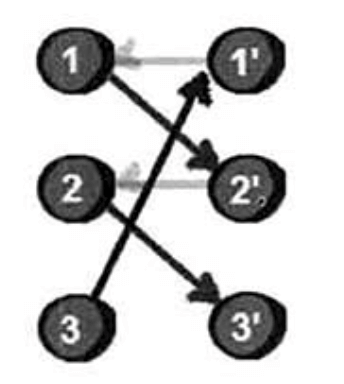
最终通过这种连锁反应,配对数从原来的2对变成了3对,增加了1对。接下来介绍两个概念:
- 交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边……形成的路径叫交替路。
- 增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发点不算),则这条交替路称为增广路。
例如上例中所得到的增广路:

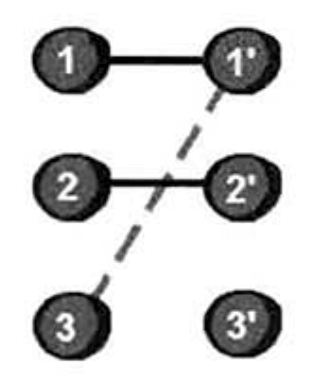
从顶点3出发,红色箭头表示未匹配边,绿色箭头表示匹配边,经过交替路后,到达另一个未匹配点3‘。增广路有一个重要特点:非匹配边比匹配边多一条(因为增广路的起点是未匹配点,与之相连的边肯定是未匹配边;增广路的终点也是未匹配点,与之相连的边也肯定是未匹配边,由交替路的定义可知,增广路从未匹配边开始,接着是匹配边,……,最后一条边还是未匹配边,所以增广路的未匹配边肯定是比匹配边多1的)。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了1条。我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。
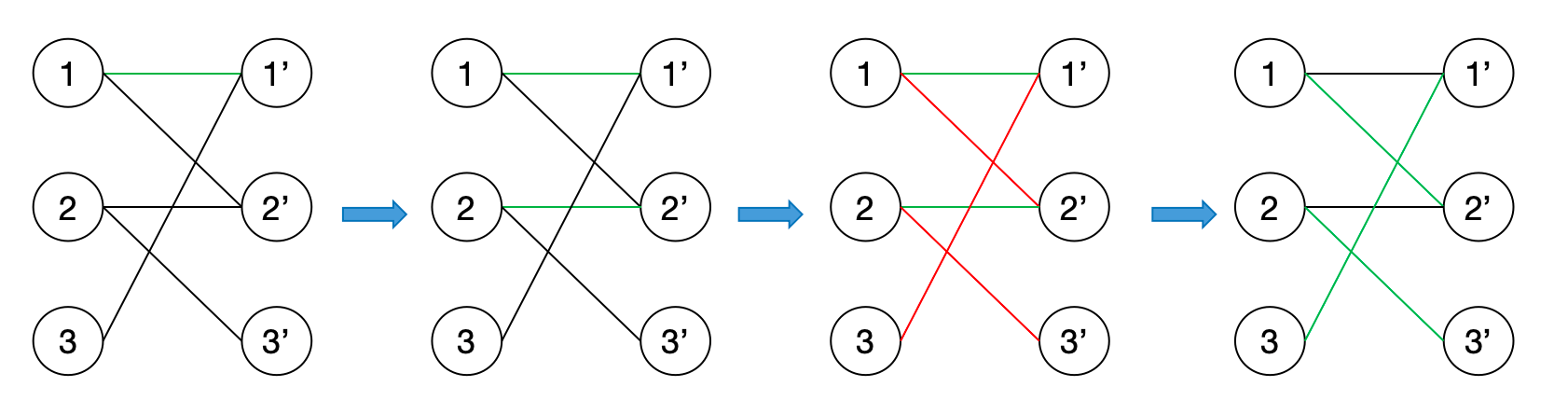
上述例子的完整过程见上图。绿色边为匹配边,红色边为未匹配边。算法整体描述见下:
- 首先从任意一个未被配对的点$u$开始,从点$u$的边中任意选一条边(假设这条边是$u \to v$)开始配对。如果此时点$v$还没有被配对,则配对成功,此时便找到了一条增广路(只不过这条增广路比较简单)。如果此时点$v$已经被配对了,那就要尝试进行“连锁反应”。如果尝试成功了,则找到一条增广路,此时需要更新原来的配对关系。这里要用一个数组match来记录配对关系,比如点$v$与点$u$配对了,就记作$\text{match} [v]=u$和$\text{match} [u]=v$。配对成功后,记得要将配对数加1。配对的过程我们可以通过深度优先搜索来实现,当然广度优先搜索也可以。
- 如果刚才所选的边配对失败,要从点$u$的边中再重新选一条边,进行尝试。直到点$u$配对成功,或者尝试过点$u$所有的边为止。
- 接下来继续对剩下没有被配对的点一一进行配对,直到所有的点都尝试完毕,找不到新的增广路为止。
- 输出配对数。
用下面动图展示一个更复杂的例子:

完整实现代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <stdio.h>
int e[101][101];
int match[101];
int book[101];
int n,m;
int dfs(int u)
{
int i;
for(i=1;i<=n;i++)
{
if(book[i]==0 && e[u][i]==1)
{
book[i]=1;//标记点i已访问过
//如果点i未被配对或者找到了新的配对
if(match[i]==0 || dfs(match[i]))
{
//更新配对关系
match[i]=u;
match[u]=i;
return 1;
}
}
}
return 0;
}
int main()
{
int i,j,t1,t2,sum=0;
scanf("%d %d",&n,&m);//n个点m条边
for(i=1;i<=m;i++)//读入边
{
scanf("%d%d",&t1,&t2);
e[t1][t2]=1;
e[t2][t1]=1;//这里是无向图
}
for(i=1;i<=n;i++)
match[i]=0;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
book[j]=0;//清空上次搜索时的标记
if(dfs(i))
sum++;//寻找增广路,如果找到,配对数加1
}
printf("%d",sum);
getchar();getchar();
return 0;
}
可以输入以下数据进行验证。注:1、2、3为女生,4、5、6为男生。
1
2
3
4
5
6
6 5
1 4
1 5
2 5
2 6
3 4
运行结果是:
1
3
如果二分图有n个点,那么最多找到n/2条增广路径。如果图中共有m条边,那么每找一条增广路径最多把所有边遍历一遍,所花时间是m。所以总的时间复杂度是$O(NM)$。该算法被称为匈牙利算法。