博客为参考《程序是怎样跑起来的》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.文件以字节为单位保存
👉第6章热身问答:
- 文件储存的基本单位是什么?
- 1字节(=8位)。文件是字节数据的集合体。
- DOC、LZH和TXT这些扩展名中,哪一个是压缩文件的扩展名?
- LZH。LZH是用LHA等工具压缩过的文件的扩展名。
- 文件内容用“数据的值$\times$循环次数”来表示的压缩方法是RLE算法还是哈夫曼算法?
- RLE算法。例如,AAABB这个数据压缩后就是A3B2。
- 在Windows计算机经常使用的SHIFT JIS字符编码中,1个半角英数是用几个字节的数据来表示的?
- 1字节(=8位)。半角英文数字是用1个字节来表示的,汉字等全角字符是用两个字节来表示的。
- BMP(BITMAP)格式的图像文件,是压缩过的吗?
- 没有压缩过。因为BMP格式的图像文件是没有被压缩的,因此要比JPEG格式等压缩过的图像文件大不少。
- 可逆压缩和非可逆压缩的不同点是什么?
- 压缩后的数据能复原的是可逆压缩,无法复原的是非可逆压缩。像照片(JPEG格式)这样,之所以压缩后也不会让人感到不自然,就是因为使用了非可逆压缩。
文件是将数据存储在磁盘等存储媒介中的一种形式。程序文件中存储数据的单位是字节。文件的大小之所以用KB、MB等来表示,就是因为文件是以字节(B=Byte)为单位来存储的$^1$。
- 正如第5章所述,从物理上对磁盘进行读写时是以扇区(512字节)为单位的。但另一方面,程序则可以在逻辑上以字节为单位对文件的内容进行读写。
文件就是字节数据的集合。用1字节(=8位)表示的字节数据有256种,用二进制数来表示的话,其范围就是00000000~11111111。如果文件中存储的数据是文字,那么该文件就是文本文件。如果是图形,那么该文件就是图像文件。在任何情况下,文件中的字节数据都是连续存储的(图6-1)。

2.RLE算法的机制
把文件内容用“数据$\times$重复次数”的形式来表示的压缩方法称为RLE(Run Length Encoding,行程长度编码)算法(图6-2)。RLE算法经常被用于压缩传真的图像等$^1$。

- RLE算法经常被用于传真FAX等。G3类传真机是把文字和图形都作为黑白图像来发送的。由于黑白图像的数据中,白或黑通常是部分连续的,因此就没有必要再发送这部分数据的值(白或者黑),而只需附带上重复次数即可,这样压缩效率就得到了大幅提升。例如,像白色部分重复5次,黑色部分重复7次,白色部分重复4次,黑色部分重复6次这样的部分图像,就可以用5746这样的重复次数数字来进行压缩。
3.RLE算法的缺点
然而,在实际的文本文件中,同样字符多次重复出现的情况并不多见。虽然针对相同数据经常连续出现的图像、文件等,RLE算法可以发挥不错的效果,但它并不适合文本文件的压缩。

压缩后同压缩前文件大小的比率,称为压缩比率或压缩比。
通过表6-1可以看出,使用RLE算法对文本文件进行压缩后,文件却增大了,而且几乎是压缩前的2倍。这是因为文本文件中同样字符连续出现的部分并不多。以存储着“This is a pen.”这14个字符的文本文件为例,使用RLE算法对其进行压缩后,就变成了“T1h1i1s1 1i1s1 1a1 1p1e1n1.1”这样的28个字符,是压缩前的2倍。由于文章中字符大量连续出现的情况并不多见,因此,使用RLE算法后,大部分字符后面都会加上1,这样一来,压缩后的文件自然变成了之前的2倍。
此外,我们也可以在RLE算法的基础上再下点功夫,不以1个字符为单位,而以字符串为单位来查找重复次数。例如,This is a pen.中,is重复了两次。通过利用这个压缩技巧,压缩后的文件也能小一些。
4.通过莫尔斯编码来看哈夫曼算法的基础
哈夫曼算法是哈夫曼(D.A. Huffman)于1952年提出来的压缩算法。压缩软件LHA使用的就是哈夫曼算法。
文本文件是由不同类型的字符组合而成的,而且不同的字符出现的次数也是不同的。例如,在某一个文本文件中,A出现了100次左右,Q仅用到了3次,类似这样的情况是很常见的。而哈夫曼算法的关键就在于“多次出现的数据用小于8位的字节数来表示,不常用的数据则可以用超过8位的字节数来表示”。A和Q都用8位来表示时,原文件的大小就是100次$\times$8位$+$3次$\times$8位$=$824位,而假设A用2位、Q用10位来表示,压缩后的大小就是100次$\times$2位$+$3次$\times$10位$=$230位。
不过有一点需要注意,不管是不满8位的数据,还是超过8位的数据,最终都要以8位为单位保存到文件中。这是因为磁盘是以字节(8位)为单位来保存数据的(图6-3)。为了实现这一处理,压缩程序的内容会复杂很多,不过作为回报,最终得到的压缩率也是相当高的。

为了更好地理解哈夫曼算法,先来看一下莫尔斯编码。莫尔斯编码是1837年莫尔斯(Samuel F.B. Morse)提出的。莫尔斯编码不是通过语言,而是通过“嗒 嘀 嗒 嘀”这些长点和短点的组合来传递文本信息的。实际上,根据字符种类的不同,莫尔斯电码符号的长度也是不同的。表6-2是莫尔斯编码的示例。大家把1看作是短点(嘀),把11看作是长点(嗒)即可。
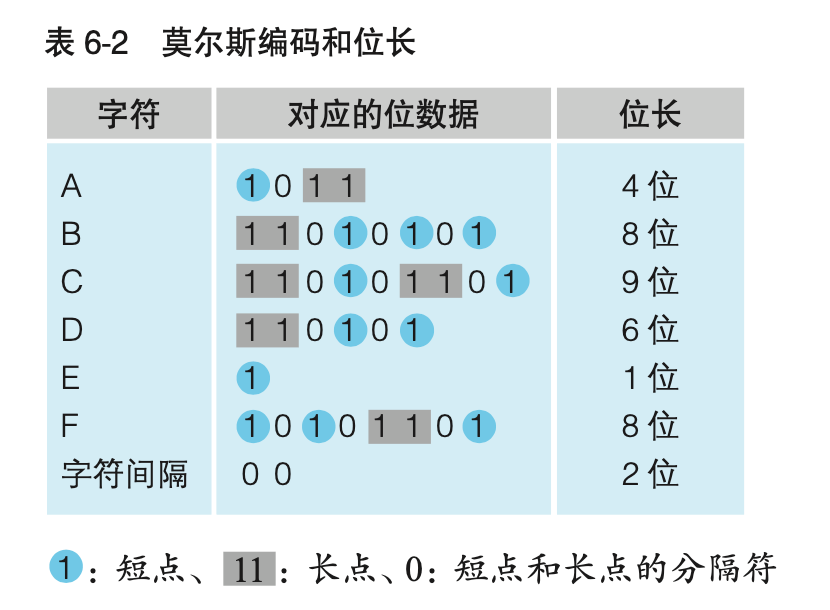
莫尔斯编码把一般文本中出现频率高的字符用短编码来表示。如表6-2所示,E这一字符的数据就可以用1位的1来表示,C这一字符的数据就可以用9位的110101101来表示。我们尝试一下用莫尔斯编码来表示AAAAAABBCDDEEEEEF这个17个字符的文本。在莫尔斯编码中,各个字符之间需要加入表示间隔的符号。这里我们用00来进行区分。因此,AAAAAABBCDDEEEEEF这个文本,就变成了A$\times$6次$+$B$\times$2次$+$C$\times$1次$+$D$\times$2次$+$E$\times$5次$+$F$\times$1次$+$字符间隔$\times$16$=$4位$\times$6次$+$8位$\times$2次$+$9位$\times$1次$+$6位$\times$2次$+$1位$\times$5次$+$8位$\times$1次$+$2位$\times$16次$=$106位$\fallingdotseq$14字节。因为文件只能以字节为单位来存储数据,因此不满1字节的部分就要圆整成1个字节。如果所有字符占用的空间都是1个字节(8位),这样文本中列出来的17个字符$=$17个字节,那么莫尔斯电码的压缩比率就是14$\div$17$\fallingdotseq$82%,并不太突出。
5.用二叉树实现哈夫曼编码
刚才已经提到,莫尔斯编码是根据日常文本中各字符的出现频率来决定表示各字符的编码的数据长度的。不过,该编码体系,对AAAAAABBCDDEEEEEF这样的特殊文本并不是最适合的。在莫尔斯编码中,E的数据长度最短,而在AAAAAABBCDDEEEEEF这个文本中,出现最频繁的是字符A。因此,应该给A分配数据长度最短的编码。这样做才会使压缩率更高。
哈夫曼算法是指,为各压缩对象文件分别构造最佳的编码体系,并以该编码体系为基础来进行压缩。因此,用什么样式的编码(哈夫曼编码)对数据进行分割,就要由各个文件而定。用哈夫曼算法压缩过的文件中,存储着哈夫曼编码信息和压缩过的数据(图6-4)。

接下来,我们尝试一下把AAAAAABBCDDEEEEEF中的A~F这些字符,按照“出现频率高的字符用尽量少的位数编码来表示”这一原则进行整理。按照出现频率从高到低的顺序整理后,结果就如表6-3所示。该表中同时也列出了编码的方案。

不过,这个编码体系是存在问题的。该问题就是,例如100这个3位的编码,它的意思是用1、0、0这3个编码来表示E、A、A呢?还是用10、0这两个编码来表示B、A呢?亦或是用100来表示C呢?这些都无法进行区分。因此,如果不加入用来区分字符的符号,这个编码(方案)就无法使用。
而在哈夫曼算法中,通过借助哈夫曼树构造编码体系,即使在不使用字符区分符号的情况下,也可以构建能够明确进行区分的编码体系。
接下来我们就来看一下如何制作哈夫曼树。自然界的树是从根开始生枝长叶的。而哈夫曼树则是从叶生枝,然后再生根。图6-5展示了对AAAAAABBCDDEEEEEF进行编码的哈夫曼树的制作过程。

6.哈夫曼算法能够大幅提升压缩比率
接下来,让我们来看一下哈夫曼算法的压缩比率。用图6-5得到的哈夫曼编码表示AAAAAABBCDDEEEEEF,结果为0000000000001001001101011010101010101111,40位=5字节(这里为不包含哈夫曼编码信息的情况)。压缩前的数据是17字符=17字节,也就是说,我们得到了5字节$\div$17字节$\fallingdotseq$29%这样高的压缩率。表6-4是将表6-1中的文件应用哈夫曼算法的LHA进行压缩后的结果。

7.可逆压缩和非可逆压缩
最后,让我们来看一下图像文件的数据形式。图像文件的使用目的通常是把图像数据输出到显示器、打印机等设备上。Windows的标准图像数据形式为BMP$^1$,是完全未压缩的。由于显示器及打印机输出的bit(点)是可以直接映射(mapping)的,因此便有了BMP=bitmap这一名称。
- BMP(Bitmap)是使用Windows自带的画笔来做成的一种图像数据形式。
除BMP格式以外,还有其他各种格式的图像数据形式。比如JPEG$^1$格式、TIFF$^2$格式、GIF$^3$格式等。与BMP格式不同的是,这些图像数据都会用一些技法来对数据进行压缩。
- JPEG(Joint Photographic Experts Group)是数码相机等常用的一种图像数据形式。
- TIFF(Tag Image File Format)是一种通过在文件头中包含“标签”就能够显示出数据性质的图像数据形式。
- GIF(Graphics Interchange Format)是由美国CompuServe开发的一种数据格式。这种格式要求色数不超过256色。
图像文件还可以使用与前文介绍的RLE算法、哈夫曼算法不同的其他压缩算法。这是因为,多数情况下,并不要求压缩后的图像文件必须还原到与压缩前同等的质量。与之相比,程序的EXE文件以及每个字符、数值都有具体含义的文本文件则必须要还原到和压缩前同样的内容。而对于图像文件来说,即使有时无法还原到压缩前那样鲜明的图像状态,但只要肉眼看不出什么区别,有一些模糊也勉强可以接受。这里,我们把能还原到压缩前状态的压缩称为可逆压缩,无法还原到压缩前状态的压缩称为非可逆压缩(图6-6)。

图6-7中列出了各种格式的图像文件。其中,原始的图像文件是BMP格式。通过此图可以看出,JPEG格式和GIF格式的图像文件有一些模糊。这是因为JPEG格式$^1$的文件是非可逆压缩,因此还原后的图像信息有一部分是模糊的。而GIF格式的文件虽然是可逆压缩,但因为有色数不能超过256色的限制,所以还原后颜色信息会有一些缺失,进而导致了图像模糊。TIFF格式的图像文件虽然不模糊,但却比原始的BMP格式的文件还要大。这是因为TIFF格式的文件中带有各种标签信息,是可以选择压缩格式的,而这里选择的是与BMP同样的无压缩方式。但由于与原始的图像数据相比,TIFF格式的文件中附加了标签信息,所以结果就比BMP格式的文件更大了。
- 数码相机中经常用到的JPEG格式文件,有3种压缩方式。
- 把构成图像的点阵的颜色信息由RGB(红色、绿色、蓝色)形式转化成YCbCr(亮度、蓝色色度、红色色度)形式。我们知道,人眼对亮度很敏感,但对颜色的变化却有些迟钝。因此,人眼比较敏感的亮度Y就是一个很重要的参数,而表示颜色的Cb、Cr则没有那么重要。于是我们就可以通过减少Cb和Cr的信息间距来缩小图像数据的大小。
- 将每个点的色素变化看作是波形的信号变化,进行傅立叶变化。傅立叶变换是指将波形按照频率分量进行分解。照片等图像文件的特点是低频率(柔和的颜色变化)的部分较多,高频率(强烈的颜色变化)的部分较少。因此,这里我们就可以把高频率的部分剪切掉。这样一来,图像数据也就会缩小。虽然剪切掉了高频率部分,但人眼分辨不出什么差别。不过,如果是用Windows画笔描绘的简单图形,其中颜色变化强烈的部分就会出现模糊现象。大家不妨使用Windows画笔做一个圆形或者四方形的图形,并将其保存成JPEG格式。然后再打开这个JPEG文件,你就会发现颜色变化强烈的部分变模糊了。
- 最后,将已经瘦身的图像数据通过哈夫曼算法进行压缩。这样就可以使图像数据进一步缩小。

压缩算法的种类大概有一二十种。之所以会存在如此多的压缩算法,是因为压缩比率、压缩需要的处理时间(程序的复杂程度)以及各种文件的需求等是不一样的。因此,至今学界都不能提出一个万能的压缩算法。