本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
源码:code。
目前SOTA的目标检测器都是two-stage的、由proposal驱动的机制。比如R-CNN框架,第一阶段生成一组稀疏的候选目标位置,第二阶段使用卷积神经网络将每个候选位置分为前景或背景。后续的two-stage框架(Fast R-CNN、Faster R-CNN、FPN、Mask R-CNN)在COCO benchmark上取得了最高精度。
two-stage检测器取得了巨大的成功,那就衍生出一个问题:一个简单的one-stage检测器能够达到类似的精度吗?最近一些one-stage框架,比如YOLO(YOLOv1、YOLOv2)和SSD,其检测精度相比之前有了很大的提升,这让我们看到了希望。
我们提出了一种新的one-stage目标检测器,其在COCO上的精度首次和复杂的two-stage检测器不相上下。阻碍one-stage检测器精度达到SOTA水平的主要原因是类别不平衡,我们提出一种新的损失函数来消除这一障碍。
像R-CNN这样的two-stage检测器,解决类别不平衡的方法有两种:1)在proposal stage(比如Selective Search、EdgeBoxes、DeepMask、RPN)快速减少候选目标位置,过滤掉大多数负样本;2)在第二个分类阶段,通常固定正负样本的采样比例(比如$1:3$)或使用hard example mining(OHEM)。
相比之下,one-stage检测器通常需要密集的生成大量的候选目标位置。虽然我们也可以在训练时固定正负样本的采样比例,但这样做是低效的。这种低效是目标检测中的一个经典问题,通常通过bootstrapping或hard example mining等技术来解决。
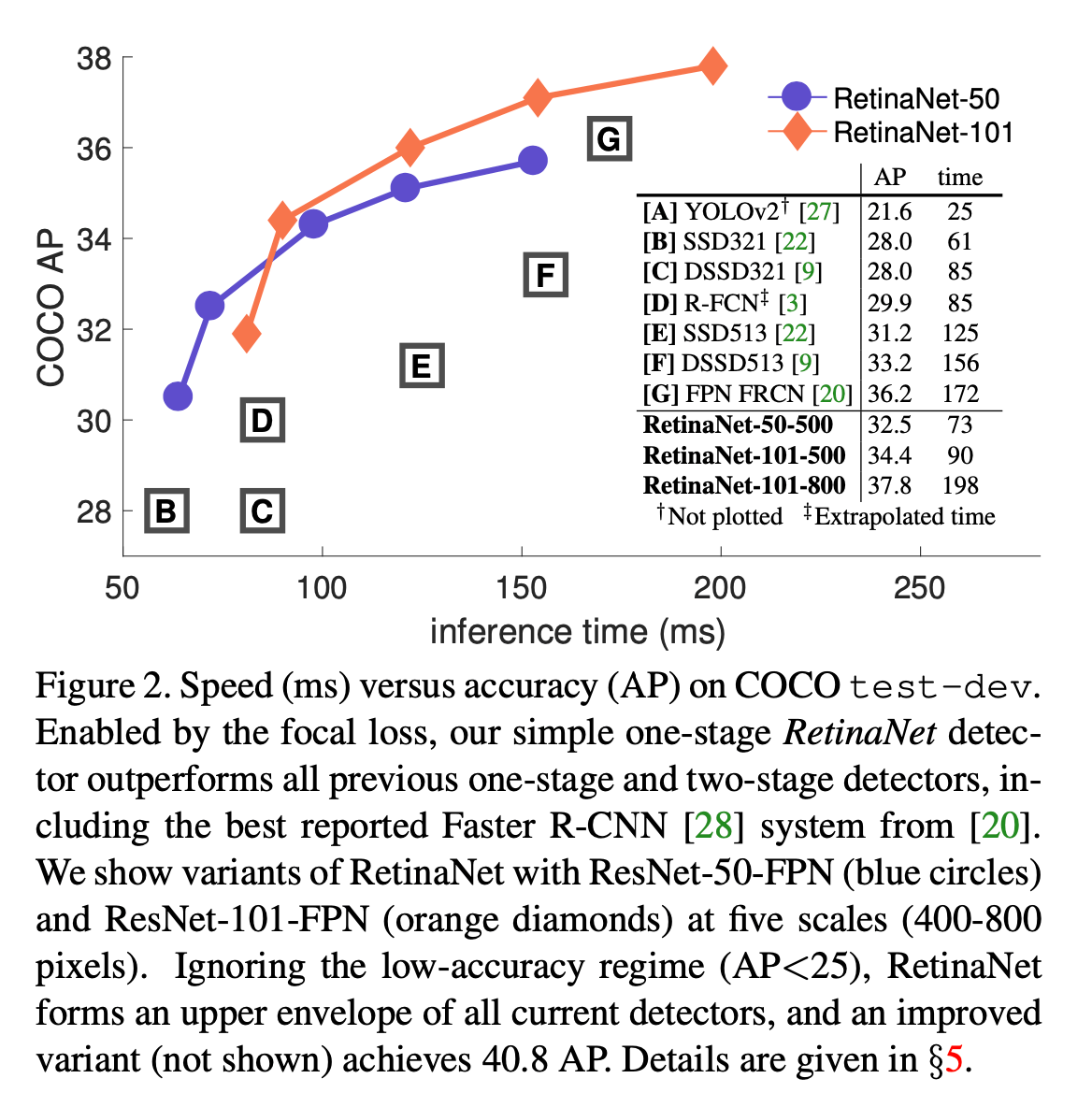
在本文中,我们提出一种新的损失函数:focal loss,可有效替代之前的技术用来解决类别不平衡问题。为了证明focal loss的有效性,我们设计了一个简单的one-stage目标检测器,称为RetinaNet,其性能优于之前所有的one-stage以及two-stage检测器,性能比较见Fig2。
2.Related Work
不再赘述。
3.Focal Loss
Focal Loss在one-stage目标检测中被用于解决训练中前景和背景类别极端不平衡(比如$1:1000$)的问题。首先我们先介绍二分类的CE loss(cross entropy loss):
\[\text{CE}(p,y) = \begin{cases} -\log (p) & \text{if} \ y=1 \\ -\log (1-p) & \text{otherwise} \end{cases} \tag{1}\]focal loss可以很容易的被扩展到多分类,为了简化,我们只介绍二分类的情况。
其中,$y \in \{ \pm 1 \}$为GT类别,$p \in [0,1]$为预测成正样本(即$y=1$)的概率。为了方便,我们定义$p_t$:
\[p_t = \begin{cases} p & \text{if} \ y=1 \\ 1-p & \text{otherwise} \end{cases} \tag{2}\]CE loss可重写为:$\text{CE}(p,y)=\text{CE} (p_t) = -\log (p_t)$。
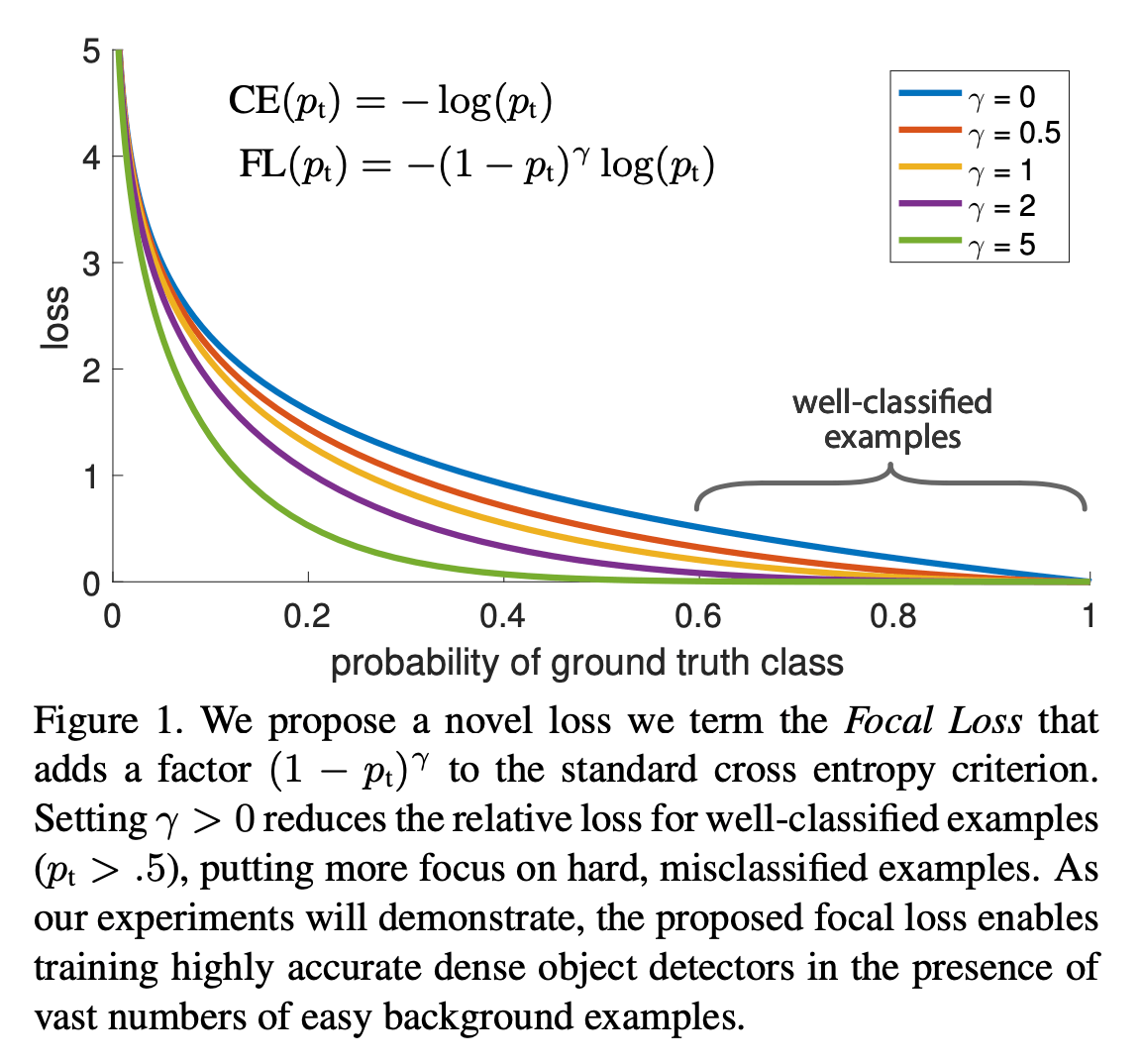
CE loss在Fig1中用最上方的蓝色曲线表示。可以看出,即使很容易分类的样本($p_t \gg .5$,通常为负样本)也会产生不小的损失。模型在学习过程中受大量简单样本(即容易被分类的样本)主导,对模型收敛影响大,影响模型分类性能。
3.1.Balanced Cross Entropy
一个常见的解决类别不平衡的方式是引入权重因子$\alpha \in [0,1]$:
\[\text{CE}(p,y) = \begin{cases} -\alpha \log (p) & \text{if} \ y=1 \\ -(1-\alpha) \log (1-p) & \text{otherwise} \end{cases}\]其中,$\alpha$可以是类别频率的倒数,也可以是通过交叉验证确定的超参数。我们将上式简写为:
\[\text{CE} (p_t) = -\alpha_t \log (p_t) \tag{3}\]3.2.Focal Loss Definition
如我们的实验所示,在dense检测器训练过程中的大量负样本主导了CE loss。容易被分类的负样本构成了loss的主要部分,并主导了梯度。虽然$\alpha$在一定程度上平衡了正/负样本,但它并没有区分简单/困难样本。因此,我们建议降低简单样本的权重,将训练的重点放在困难的负样本上。
我们在CE loss中加入调控因子(modulating factor):$(1-p_t)^{\gamma}$,其中$\gamma \geqslant 0$。focal loss的定义见下:
\[\text{FL}(p,y) = \begin{cases} -(1-p)^{\gamma}\log (p) & \text{if} \ y=1 \\ -p^{\gamma}\log (1-p) & \text{otherwise} \end{cases}\]可简写为:
\[\text{FL} (p_t) = -(1-p_t)^{\gamma} \log (p_t) \tag{4}\]$\gamma \in [0,5]$的可视化见Fig1。从中可以看出focal loss的两个性质。可以在式(4)的基础上再加入$\alpha$权重因子:
\[\text{FL} (p_t) = -\alpha_t (1-p_t)^{\gamma} \log (p_t) \tag{5}\]在我们的实验中,式(5)的精度比式(4)要高一点点。
3.3.Class Imbalance and Model Initialization
默认情况下,二分类模型被初始化后,预测$y=-1$或$y=1$的概率基本相等。在这样的初始化下,当存在类别不平衡时,高频类别的损失会主导总损失,并导致早期训练的不稳定。为了应对这种情况,在训练初期,我们为模型对低频类别的预测$p$值引入了“先验”的概念。我们用$\pi$表示这个“先验”,将其设置为使得模型对低频类别的预测$p$值较低,比如0.01。我们发现,在严重类别不平衡的情况下,这一操作可提高CE和focal loss的训练稳定性。
3.4.Class Imbalance and Two-stage Detectors
two-stage检测器通常使用CE loss,并不引入$\alpha$权重因子或使用focal loss。相反,它们通过两种机制来解决类别不平衡问题:1)两阶段级联;2)有偏的minibatch采样。第一个级联阶段是object proposal机制,将几乎无限多的候选检测位置降低到一两千个。在第二阶段训练时,通常使用有偏抽样来构成minibatch,比如正负样本的比例控制为$1:3$。这个采样比例就像一个隐含的$\alpha$权重因子。而我们提出的focal loss则可直接用于one-stage检测器,通过损失函数来解决类别不平衡问题。
4.RetinaNet Detector
RetinaNet包括一个backbone和两个task-specific的子网络,见Fig3。
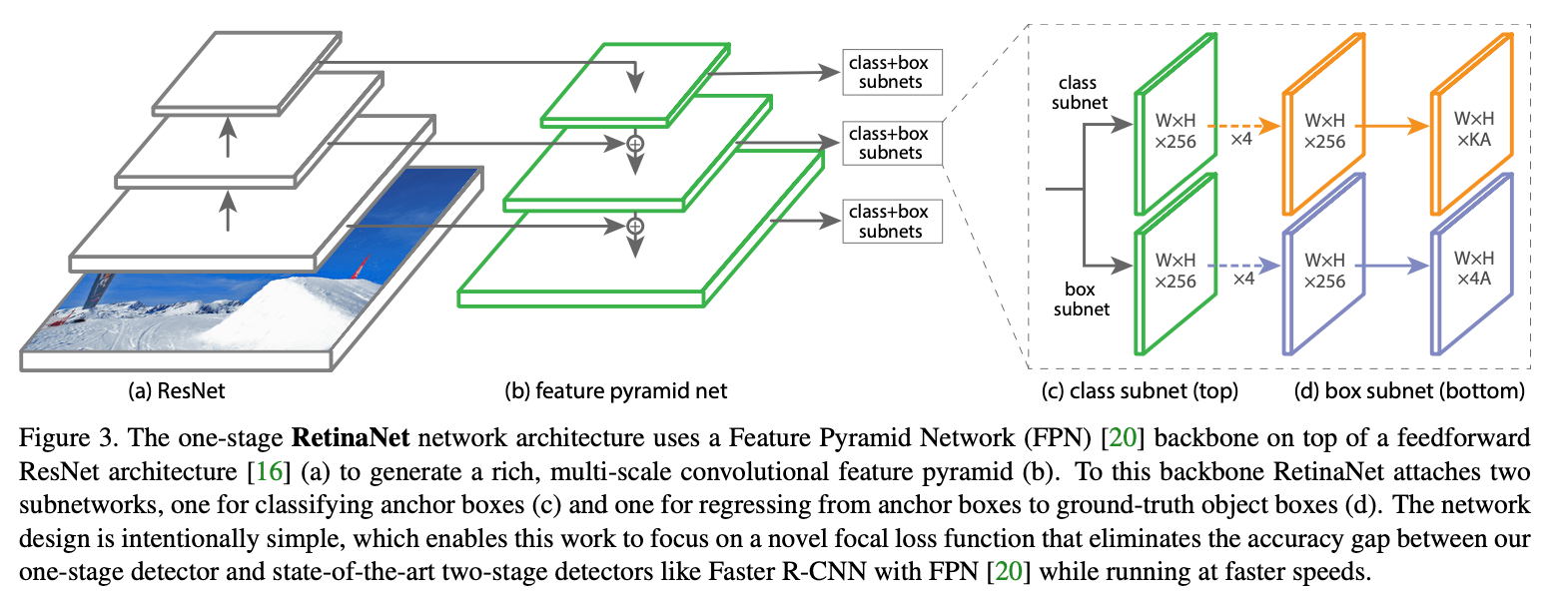
👉Feature Pyramid Network Backbone:
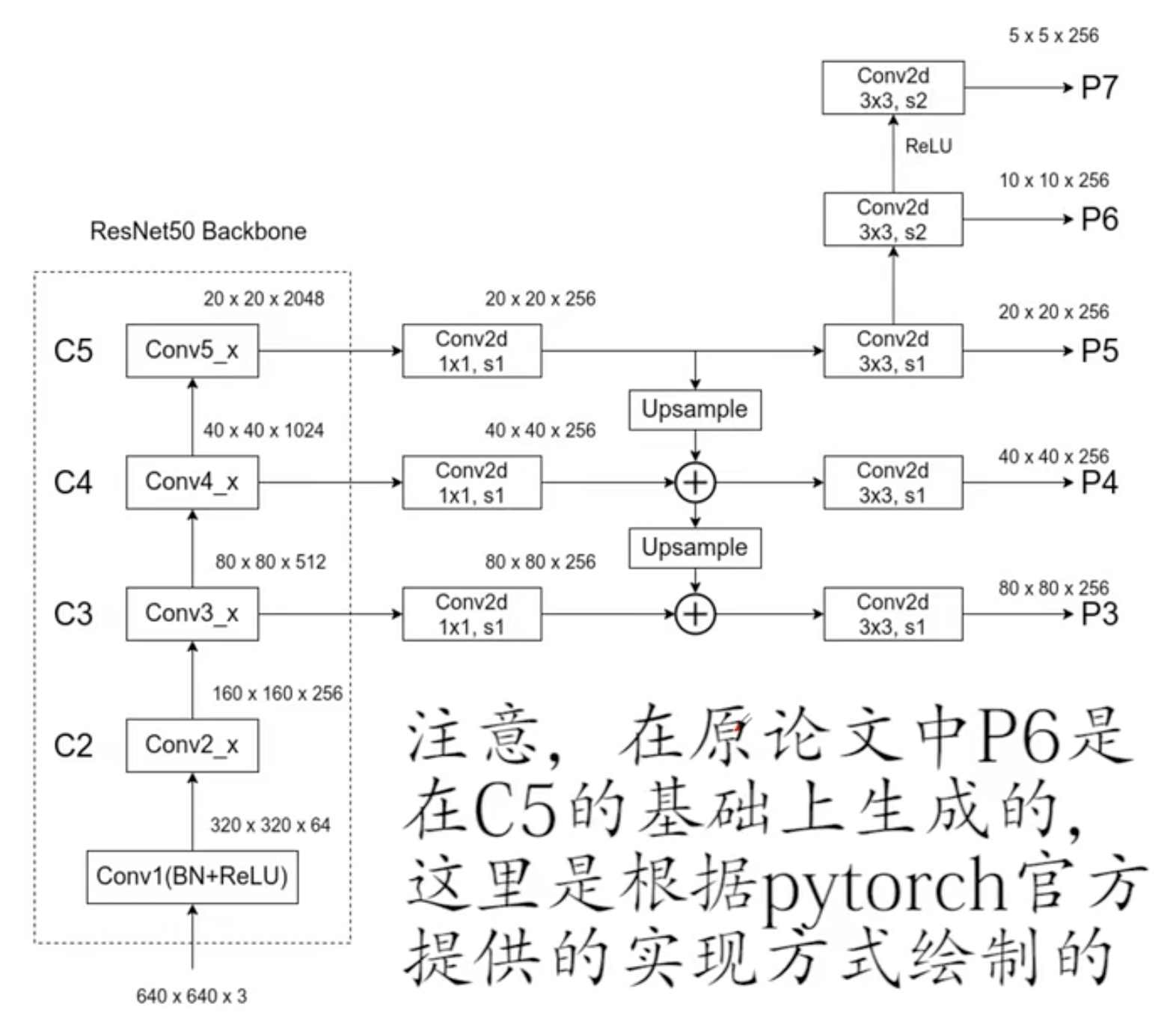
我们使用FPN作为RetinaNet的backbone。FPN的构建基于ResNet。使用$P_3-P_7$构建金字塔,其中$P_3-P_5$对应ResNet的$C_3-C_5$,对$C_5$进行步长为2的$3\times 3$卷积从而进一步得到$P_6$,在$P_6$上使用步长为2的$3 \times 3$卷积以及ReLU函数从而得到$P_7$。相比FPN原文:1)我们没有使用高分辨率的$P_2$;2)$P_6$的计算是通过带步长的卷积,而不是下采样;3)我们引入$P_7$来提升对大目标的检测。这些小修改在保持精度的同时提升了速度。所有金字塔层级的通道数都固定为$C=256$。backbone的详细结构图:
👉Anchors:
从$P_3-P_7$,每一层级的anchor设置见下:

如上所示,金字塔的每一层级对应$A=9$种anchor。
每个anchor分配一个长度为$K$的one-hot向量($K$为类别数)以及一个表示bbox的长度为4的向量。我们使用RPN中的分配规则,但针对多类别检测进行了修改,并调整了阈值。和前景GT box的IoU大于0.5的anchor被视为正样本,IoU在$[0,0.4)$之间的被视为负样本,其余anchor在训练过程中会被忽略。每个anchor最多分配给一个GT box。
👉Classification Subnet:
class subnet预测每个网格的$A$个anchor分别属于$K$个类别的概率。class subnet是一个小型FCN,附加在每个FPN层级之后,不同层级之间的subnet是共享参数的。subnet的设计很简单。输入为每个金字塔层级进来的通道数为$C$的feature map,接着是4个$3\times 3$卷积层(每层卷积核数量为$C$个,激活函数为ReLU),最后一层还是一个$3\times 3$卷积层,但卷积核数量为$KA$个。在大多数实验中,设$C=256,A=9$。
和RPN相比,我们的class subnet更深,且只使用了$3\times 3$卷积,并且没有和box subnet共享参数。
👉Box Regression Subnet:
类似class subnet,box subnet是与其平行的一个小型FCN。box subnet和class subnet的设计基本一致,除了最后一层卷积核的数量为$4A$。每个box预测的4个参数和R-CNN中的一致。和最近的研究不同,我们的bbox预测没有和类别绑定在一起,这样使用更少的参数,但同样有效。
4.1.Inference and Training
👉Inference:
为了提升推理速度,对于每个FPN层级,我们只对排名前1k(个人理解就是分类概率值最高,即最有可能包含有目标)的anchor预测bbox。所有层级预测的bbox会通过NMS(阈值为0.5)汇总在一起得到最终的预测结果。
👉Focal Loss:
class subnet的输出使用focal loss。我们通过实验发现$\gamma = 2$时模型性能比较好,当$\gamma \in [0.5,5]$时,RetinaNet相对稳健。在训练RetinaNet时,focal loss应用于每个采样图像中所有约100k个anchor上。这与使用启发式采样(heuristic sampling,比如RPN)或hard example mining(比如OHEM和SSD)是截然不同的,后者在计算loss时只考虑一个minibatch内的anchor(比如256个)。一幅图像总的focal loss为该图像所有~100k个anchor的focal loss之和,并通过分配给GT box的anchor数量进行归一化。我们使用被分配的anchor数量进行归一化,而不是使用总的anchor数量进行归一化,这是因为绝大多数的anchor都是容易被正确分类的负样本,其对loss的贡献可以忽略不计。最后,我们注意到权重因子$\alpha$也有一个稳定范围,但它与$\gamma$相互影响,因此需要一起考虑(见表1(a)和表1(b))。经过我们实验,$\alpha=0.25,\gamma=2$效果最好。
👉Initialization:
我们实验了ResNet-50-FPN和ResNet-101-FPN。两者都在ImageNet1k上进行了预训练。FPN部分参照其原文进行初始化。在RetinaNet subnet中,除了最后一层,其余卷积层初始化都使用bias $b=0$和高斯权重($\sigma=0.01$)。对于class subnet的最后一层,将bias初始化为$b=-\log ((1-\pi) / \pi)$,在训练开始阶段,每个anchor都应该被标记为前景,且置信度约为$\pi$。在所有实验中,我们都设$\pi=.01$。如在第3.3部分中所描述的那样,这种初始化是为了防止大量属于背景的anchor在训练的第一次迭代中产生大且不稳定的loss值。
👉Optimization:
RetinaNet训练使用SGD。我们在8块GPU上使用synchronized SGD,一个minibatch包含16张图像(每块GPU上2张图像)。除非特殊说明,所有模型都是训练了90k次迭代,初始学习率为0.01,在第60k和第80k迭代时学习率缩小10倍。除非特殊说明,数据增强只使用了水平图像翻转。weight decay为0.0001,momentum为0.9。训练loss是focal loss(用于分类)和L1 loss(用于bbox回归)之和。表1(e)中的模型训练时长在10-35个小时之间。
5.Experiments
在COCO benchmark上进行了实验。使用COCO trainval35k split(即train split中的80k张图像用于训练,val split共包含40k张图像,随机抽出35k张用于验证)。val split剩余的5k张图像(即minival split)用于lesion和sensitivity研究。我们的主要结果在test-dev split上测试得到。
5.1.Training Dense Detection
我们进行了大量的实验来分析dense预测的损失函数以及各种优化策略。对于所有实验,我们都使用ResNet+FPN的结构。对于所有的消融实验,我们都使用600个像素的图像scale(即把图像短边resize到600个像素)来进行训练和测试。
👉Network Initialization:
我们首先尝试了使用标准的CE loss训练RetinaNet,并且不修改初始化或学习策略。但模型在训练过程中一直不收敛。然而,如果简单的初始化模型的最后一层,使检测到目标的先验概率为$\pi=.01$(见第4.1部分),模型就可以得到有效的训练。使用这种初始化策略,RetinaNet(backbone为ResNet-50)在COCO上取得了30.2的AP。结果对$\pi$的取值并不敏感,所以在所有实验中我们都设$\pi = .01$。
👉Balanced Cross Entropy:
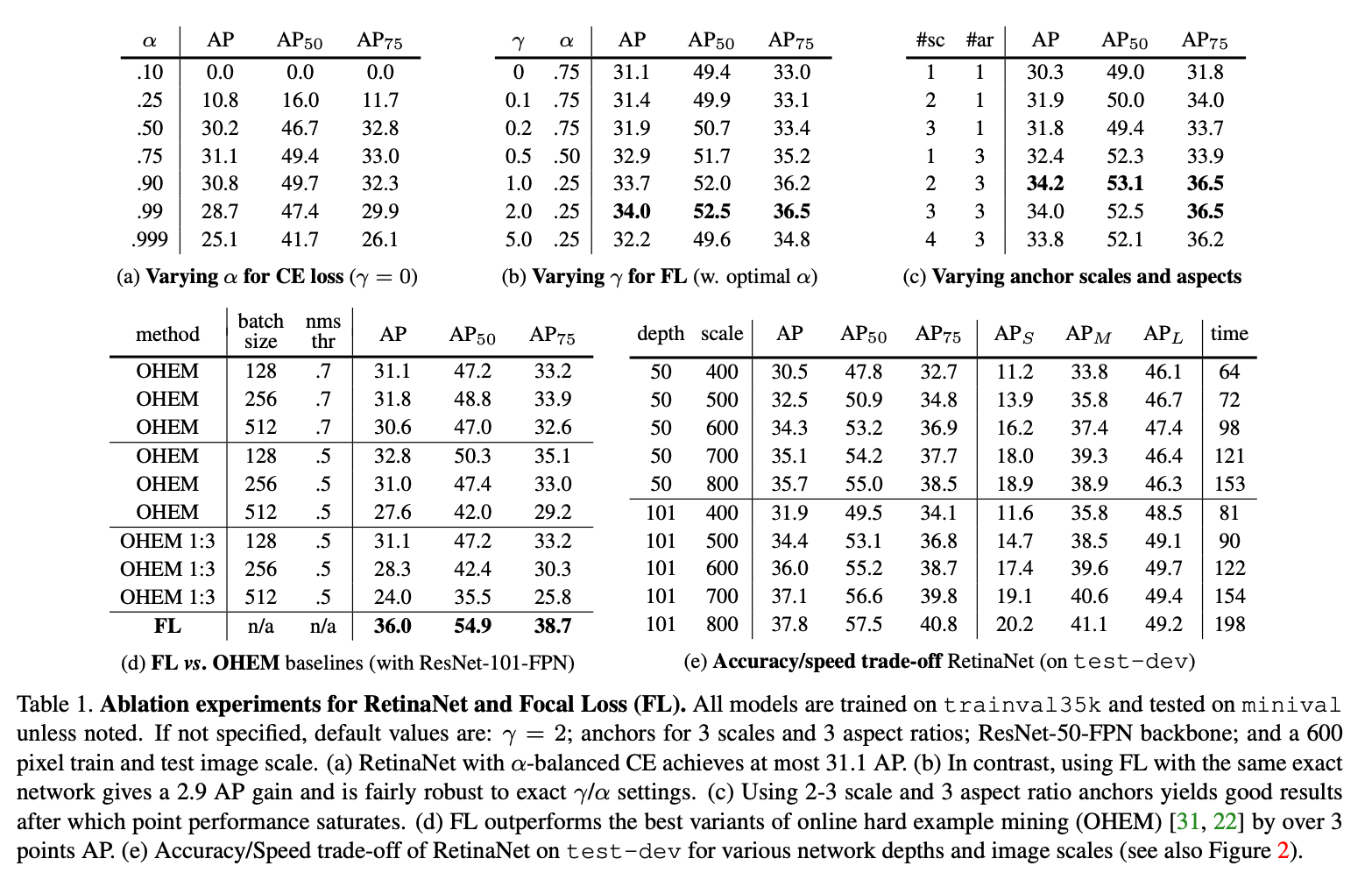
$\alpha$-balanced CE loss的测试结果见表1(a)。
👉Focal Loss:
focal loss的测试结果见表1(b)。为了公平的比较,对于每个$\gamma$,我们都匹配了其最优的$\alpha$。我们可以发现,较大的$\gamma$通常会选择较小的$\alpha$。总的来说,优化$\gamma$的收益更大,较优的$\alpha$区间为$[.25,.75]$(我们测试了$\alpha \in [.01,.999]$)。在所有实验中,我们都设$\gamma=2.0,\alpha=.25$,但是如果设$\alpha=.5$其实性能也差不多(低了.4的AP)。
👉Analysis of the Focal Loss:
为了更好的理解focal loss,我们分析了收敛模型损失的经验分布。实验所用模型的backbone为ResNet-101,输入图像短边长为600个像素,$\gamma=2$(AP为36.0)。基于大量随机图像,我们采集了$\sim 10^7$个负样本窗口和$\sim 10^5$个正样本窗口。然后我们计算这些样本的focal loss,并分别对正样本和负样本的loss做归一化,使其总和为1。对于归一化后的loss,我们从低到高进行排序,并绘制其累计分布函数(cumulative distribution function,CDF),见Fig4。

如果我们看正样本的曲线(见Fig4左),我们发现不同$\gamma$值的CDF看起来很相似。比如,大约20%最难预测的正样本的loss占总loss的一半,随着$\gamma$的增加,更多的loss集中在这20%最难预测的正样本上。
解释一下上面这段话,如果一个样本计算所得的loss越大,说明这个样本是难以预测正确的样本,属于hard sample。在计算CDF时,我们是从最低loss一点点往最高loss累加的,最终得到的总loss就是1,也就是说,在Fig4中,纵轴约接近1,样本的loss越大,越难以预测正确。以Fig4左为例,横轴0.8~1.0区间这20%的样本占据了将近50%的loss,属于是最难预测正确的一部分样本,并且$\gamma$越大,这个比重越大。这样的话,模型在训练时,就会想方设法的降低这些hard sample的loss(因为这些hard sample产生的loss多,所以会优先降低它们的loss),这样就能提升模型的性能了。而普通的CE loss,相比FL,其hard sample的loss较低,不利于模型学习。
$\gamma$对负样本的影响是截然不同的,见Fig4右。当$\gamma=0$时,正样本和负样本的CDF看起来差不多。然而,随着$\gamma$的增加,更多的权重集中在hard的负样本上。当$\gamma=2$(默认设置)时,绝大部分的loss来自少部分样本。可以看出,FL可以弱化easy负样本的影响,将所有注意力集中在hard负样本上。
👉Online Hard Example Mining (OHEM):
论文“A. Shrivastava, A. Gupta, and R. Girshick. Training region-based object detectors with online hard example mining. In CVPR, 2016.”提出了使用high-loss的样本来构建minibatch以提升对two-stage检测器的训练。具体来说,在OHEM中,每个样本都根据其loss进行打分,然后应用NMS,最后用loss最高的样本构建minibatch。NMS阈值和batch size都是可调的参数。与focal loss类似,OHEM也更强调预测错误的样本,但与FL不同的是,OHEM完全抛弃了easy样本。我们还实现了SSD中使用的OHEM变体:在将NMS应用于所有样本后,强制minibatch中正负样本的比例为$1:3$,从而确保每个minibatch中都有足够的正样本。
我们在one-stage检测框架中测试了两种OHEM变体,结果见表1(d)。
👉Hinge Loss:
我们也尝试用hinge loss来训练模型。然而训练并不稳定,我们没能取得有意义的结果。更多损失函数的探索见附录。
5.2.Model Architecture Design
👉Anchor Density:
one-stage检测模型中最重要的一个因素是检测框的密度。在表1(c)中,我们测试了不同anchor数量对模型性能(backbone使用ResNet-50)的影响。”#sc”为scale,一共测试了4种尺度:$2^{k/4},k \leqslant 3$;”#ar”为长宽比,一共测试了3种长宽比:0.5(即1:2)、1(即1:1)、2(即2:1)。最终我们选择了3种scale+3种长宽比。
此外,我们还可以注意到,当一个grid拥有的anchor数量超过9个时,性能并没有继续提升。
👉Speed versus Accuracy:
更大的backbone网络可以带来更高的精度,但也会拖慢推理速度。同样的还有输入图像的scale(即短边长度)。测试结果见表1(e)和Fig2。Fig2中,RetinaNet-101-500表示模型backbone为ResNet-101-FPN,输入图像scale为500。表1(e)推理速度的测试基于Nvidia M40 GPU。
5.3.Comparison to State of the Art
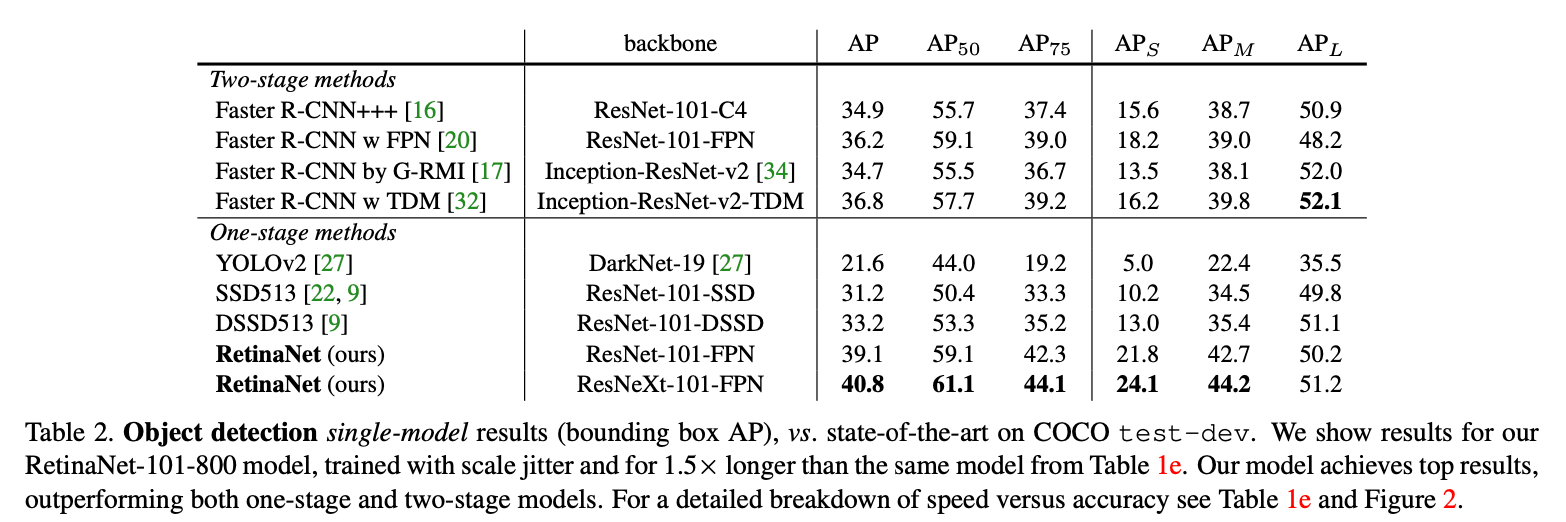
6.Conclusion
开源代码地址:链接。
7.Appendix
7.1.Appendix A: Focal Loss*
focal loss的具体形式并不重要。我们在这里展示了focal loss的另一种实现形式,它具有相似的特性,并产生了可比较的结果。接下来是对focal loss特性的更多见解。
首先,我们以与正文略有不同的形式来考虑CE和FL。具体来说,我们定义$x_t$:
\[x_t = yx \tag{6}\]其中,$y \in \{ \pm 1 \}$是类别的GT,则:
\[p_t = \sigma (x_t) = \frac{1}{1+e^{-yx}}\]结合sigmoid函数的曲线,我们可以得到当$y=1,x>0$时,$p_t>0.5$,此时正样本分类正确,当$y=-1,x<0$时,$p_t<0.5$,此时负样本分类正确,因此,只要分类正确,就有$x_t>0$。
我们现在用$x_t$定义focal loss的另一种形式:
\[p_t^* = \sigma (\gamma x_t + \beta) \tag{7}\] \[\text{FL}^* = -\log (p_t^*) / \gamma \tag{8}\]$\text{FL}^{*}$有两个参数,$\gamma$和$\beta$,分别控制loss曲线的陡度(steepness)和移动(shift)。loss曲线比较见Fig5。
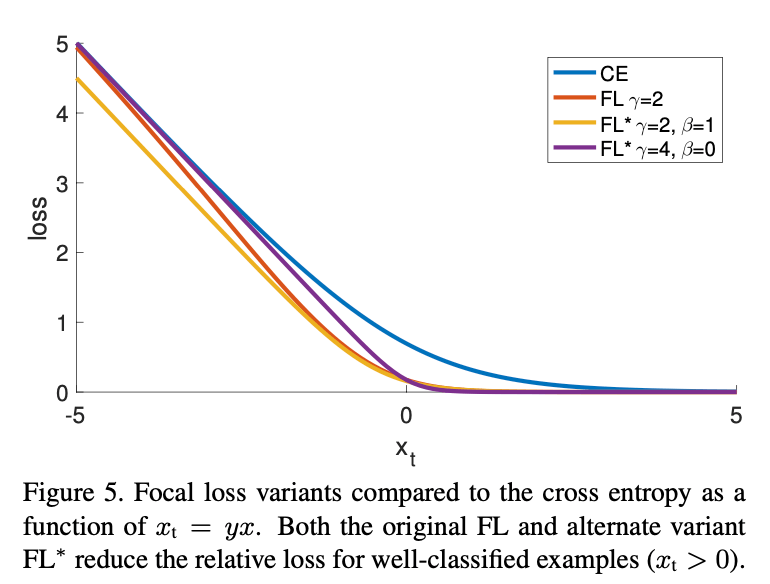
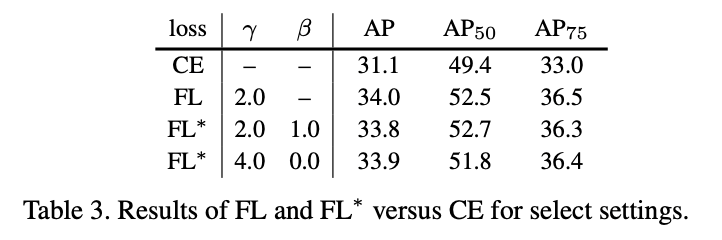
使用RetinaNet-50-600的测试结果见表3。
更广泛的$\gamma,\beta$取值测试结果见Fig7。
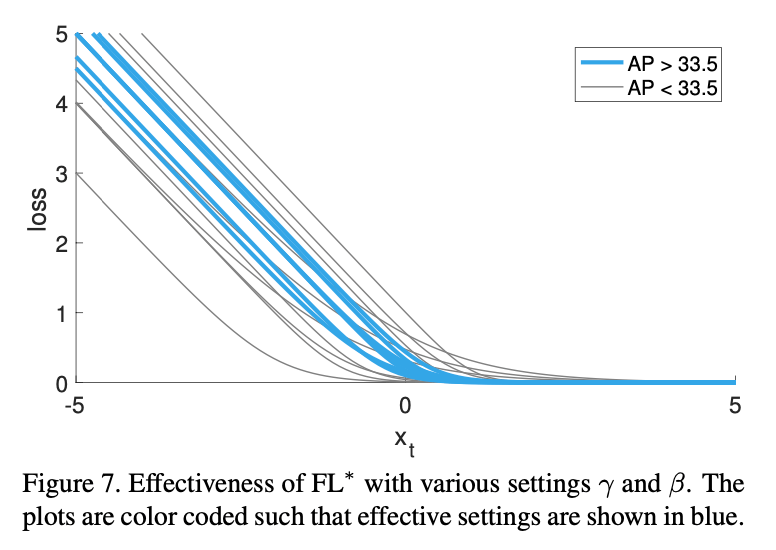
可以看出,$\text{FL}^{*}$同样有效。
7.2.Appendix B: Derivatives
损失函数的导数计算:
\[\frac{d \text{CE}}{dx} = y(p_t - 1) \tag{9}\] \[\frac{d \text{FL}}{dx} = y(1-p_t)^{\gamma}(\gamma p_t \log (p_t) + p_t - 1) \tag{10}\] \[\frac{d \text{FL}^*}{dx} = y (p_t^* - 1) \tag{11}\]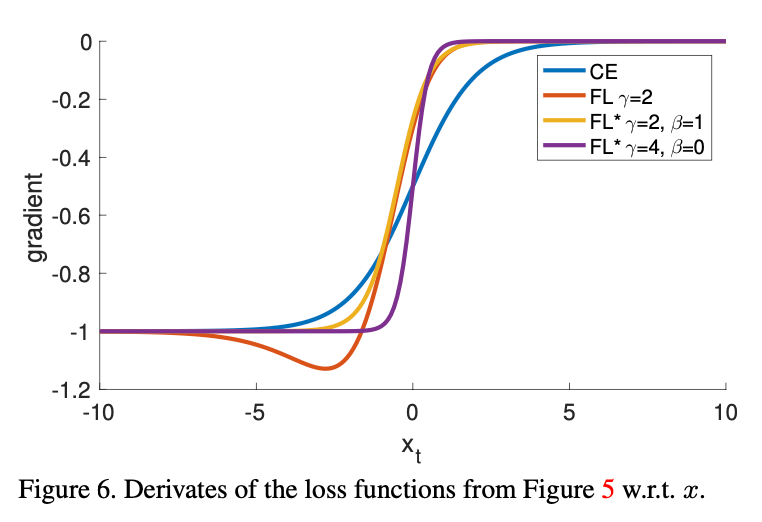
如上所有的损失函数,对于高置信度的预测,导数都趋向于-1或0。
8.原文链接
👽Focal Loss for Dense Object Detection