本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
遮挡仍然是HPE(Human Pose Estimation)面临的挑战之一,尤其是身体远端的关键点(比如手腕和脚踝),因其通常有很大的活动自由度,所以经常被遮挡。
HPE和其他检测任务通常存在一个问题,即在训练集上训练好的模型,在测试集上经常会出现明显的性能下降。举个我们的例子,在HPE中,测试集的遮挡方式可能和训练集很不一样,这导致了极大的性能下降。我们在训练集上的平均预测准确率为95.5%,但是在测试集上只有67%。如果只考虑身体远端的关键点,这个下降更加明显,从95.3%掉到了57%。
为了解决这种性能下降,或者说是泛化问题,我们需要考虑两个问题:(1)如何判断预测是否准确?这是很难的,因为测试样本并没有标签,因此无法计算预测误差。(2)如何纠正预测误差?现在的模型都是在训练集上训练完毕后,在测试时冻结网络权重,只做前向传播过程,并没有机制通过测试样本的反馈来纠正预测误差或调整网络模型。
为了解决上述问题,我们提出了SCAI(Self-Correctable and Adaptable Inference)方法。
2.Related Work
不再详述。
3.Method
我们首先展示SCAI如何解决通用网络学习和预测中的泛化问题。其次,我们会介绍如何将其应用到HPE。
3.1.Self-Correctable and Adaptable Inference
(1)Overview.

预测网络$\mathbf{\Phi}$的输入是$u$,输出是$\hat{v}$,即$\hat{v}= \mathbf{\Phi}(u)$,此外,$v$是真实值。误差校正网络$\mathbf{C}$的目的是学到一个$\Delta v$,对$\hat{v}$进行校正,校正之后的结果是$\tilde{v}$,即$\tilde{v}=\hat{v}+\Delta v$,这一步是为了提高在测试样本上的预测准确性。误差校正网络$\mathbf{C}$的另一个输入是自参考反馈误差(self-referential feedback error)$e_s$,其是FFN(误差反馈网络,Fitness Feedback Network) $\mathbf{\Gamma}$的输出,$\mathbf{\Gamma}$的输入为$u$和$\tilde{v}$。$e_s$被用作重要的反馈,以引导$\mathbf{C}$对预测结果进行自适应校正。此外,$e_s$还可用于定义损失函数,以在推理阶段快速调整和优化网络模型,使模型可以在推理阶段进行学习。
(2)Self-Correctable Inference.
网络$\mathbf{\Phi}$已经在训练集上训练好了,但其在测试集上的性能可能会有所下降。网络$\mathbf{\Phi}$在推理阶段不再更新,仅作前向传播得到$\hat{v}=\mathbf{\Phi}(u)$。正如上面所讨论的,网络$\mathbf{C}$通过预测得到的$\Delta v$将$\hat{v}$纠正为$\tilde{v}$:
\[\Delta v = \mathbf{C}(\hat{v} \mid e_s), \quad \tilde{v} = \hat{v} + \Delta v \tag{1}\]$e_s$对网络$\mathbf{C}$非常重要,如果没有了$e_s$,网络$\mathbf{C}$就无法实现任何性能改进。
那么我们该如何得到一个对网络$\mathbf{C}$有用的$e_s$呢?为了解决这个问题,我们引入了网络$\mathbf{\Gamma}$。该网络的目的是为了评估纠正后的$\tilde{v}$有多好。注意,此时我们并不知道GT,即$v$的值(也就无法衡量$\tilde{v}$和$v$之间的误差有多大)。我们的想法是将预测结果映射回原始输入域,比较原始输入域的GT和映射结果之间的差异。网络$\mathbf{\Gamma}$有两个输入:
\[e_s = \mathbf{\Gamma}(\tilde{v},u) \tag{2}\]从Fig3可以看出,通过成功的训练,$e_s$和预测误差高度相关,因此我们可以用$e_s$作为反馈来指导对预测结果的纠正。
(3)Self-Adaptable Inference.
反馈误差$e_s$具有自参考性,也就是说,$e_s$的计算并不需要GT的参与。我们只需要预测网络$\mathbf{\Phi}$、误差反馈网络$\mathbf{\Gamma}$、误差校正网络$\mathbf{C}$以及原始输入。这意味着我们可以在推理阶段计算$e_s$。一旦计算了$e_s$,其范数就可以用作损失函数,在推理阶段使用梯度反向传播来快速调整和优化网络$\mathbf{C}$。在推理阶段,网络$\mathbf{\Phi}$和$\mathbf{\Gamma}$是不更新的。需要注意的是,这种调整和优化仅适用于当前测试样本,当然也可以扩展到一个batch的测试样本以降低复杂性。接下来,我们以HPE任务为例,进一步具体解释SCAI方法。
3.2.SCAI for Human Pose Estimation
那么我们该如何将这一套预测-反馈-校正的机制应用在HPE任务上呢?

(1)Structural groups of body keypoints.
假设有输入RGB图像$I$,大小为$W \times H \times 3$。预测得到$K$个关键点:$X = \{ X_1,X_2,…,X_K \}$。基于heatmap的方法通常会预测得到$K$个大小为$W’ \times H’$的heatmap:$\{ H_1, H_2, … , H_K \}$。
为了通用性,我们将人体关键点分成了6组,见Fig2(a)。每组关键点都分成两种,一种是远端关键点,即$X_D$;另一种是近端关键点,即$X_A,X_B,X_C$。我们发现因远端关键点有着更大的活动自由度,从而经常被遮挡,导致其预测误差更大。我们的主要目标是利用SCAI方法来提高这些远端关键点的预测精度和泛化能力。
(2)SCAI Network Design.
首先,我们通过一个baseline模型(比如HRNet)预测得到一组heatmap $\{ H_A,H_B,H_C,H_D \}$,我们的目标是refine $\{ H_B,H_C,H_D \}$。我们这里先只考虑refine $H_D$(即关键点$X_D$)作为一个例子。网络$\mathbf{\Phi}$的输入是$u= \{ H_A,H_B,H_C \}$,输出是$\hat{v}=\hat{H}_D$。网络$\mathbf{C}$被用来对结果进行refine,最后得到$\tilde{v}=\tilde{H}_D$。FFN $\mathbf{\Gamma}$的输出$e_s$用来指导误差纠正。整体流程见Fig2(b)。
\[\hat{H}_D = \mathbf{\Phi}(H_A,H_B,H_C)\] \[\tilde{H}_D = \hat{H}_D + \mathbf{C}(\hat{H}_D \mid e_s) \tag{3}\] \[e_s = \mathbf{\Gamma}([H_A,H_B,H_C],\tilde{H}_D) \tag{4}\]接下来的实验,我们证明了$e_s$的L2-norm和实际网络预测误差高度相关。在这次HPE实验中,我们使用了400个batch(共25600个测试样本)来展示这种相关性。在Fig3中,每个点代表一个batch,纵轴是batch内所有关键点预测精度的平均,横轴是对应的自参考误差的平均。我们从Fig3可以看到很强的相关性,对应的相关系数为-0.84。

(3)SCAI Network Training.
在训练阶段,关键点的GT记为$\{ H^*_A,H^*_B,H^*_C,H^*_D \}$。网络$\mathbf{\Phi}$的损失函数定义为:
\[\mathcal{L}_{\mathbf{\Phi}}= \parallel \hat{H}_D - H^*_D \parallel_2\]对于网络$\mathbf{\Gamma}$,我们需要把预测结果$\tilde{H}_D$映射回原始输入域$\{ H_A,H_B,H_C \}$,并和原始输入进行比较。我们的做法是,让网络$\mathbf{\Gamma}$使用$H_B,H_C,\tilde{H}_D$作为输入,预测$H_A$,假设得到的预测结果为$\hat{H}_A$,我们就可以通过衡量$H_A$和$\hat{H}_A$的差距来判断纠正结果$\tilde{H}_D$的可靠程度了。因此,我们将$\mathbf{\Gamma}$的损失函数定义为:
\[\mathcal{L}_{\mathbf{\Gamma}} = \parallel \hat{H}_A - H^*_A \parallel _2\]网络$\mathbf{C}$的损失函数为:
\[\mathcal{L}_{\mathbf{C}} = a \cdot \mathcal{L}_{\mathbf{C}}^0 + b \cdot \mathcal{L}_{\mathbf{C}}^1 + \lambda \cdot (\mathcal{L}_{\mathbf{C}}^1 - \mathcal{L}_{\mathbf{C}}^2) \tag{5}\]其中,
\[\mathcal{L}_{\mathbf{C}}^0 = \parallel \tilde{H}_D - H^*_D \parallel_2\] \[\mathcal{L}_{\mathbf{C}}^1 = \parallel \hat{H}_A - H^*_A \parallel_2\] \[\mathcal{L}_{\mathbf{C}}^2 = \parallel \bar{H}_A - H^*_A \parallel_2\]$a,b,\lambda$是各个loss的权重。如果让网络$\mathbf{\Gamma}$使用$H_B,H_C,\hat{H}_D$作为输入,则把得到的$H_A$的预测结果记为$\bar{H}_A$。$\mathcal{L}_{\mathbf{C}}^1$和$\mathcal{L}_{\mathbf{C}}^2$唯一的区别在于,一个使用了纠正前的$\hat{H}_D$,一个使用了纠正后的$\tilde{H}_D$,如果纠正后的$\tilde{H}_D$更好,那么$\mathcal{L}_{\mathbf{C}}^1$的值会更小,从而$\mathcal{L}_{\mathbf{C}}^1-\mathcal{L}_{\mathbf{C}}^2$为负,损失值降低,因而促进网络$\mathbf{C}$的训练。
首先是预训练模型,使用训练样本来预训练网络$\mathbf{\Phi}$,即$\{ [(H_A,H_B,H_C) \to H_D] \}$。同样,也是用训练样本来预训练FFN网络,即$\{ [(H_B,H_C,H_D) \to H_A] \}$。这里的$\to$表示网络预测。在正式训练阶段,预训练过的$\mathbf{\Phi}$是不更新的。预训练过的FFN网络被用来初始化$\mathbf{\Gamma}$,使用式(5)作为损失函数,在正式训练过程中对网络$\mathbf{\Gamma}$和$\mathbf{C}$进行更新。
(4)Self-referential Adaptable Inference for Human Pose Estimation.
自参考误差的计算仅依赖输入样本,而不需要任何身体关键点的GT。因此,在推理阶段,我们使用自参考误差作为损失函数来更新网络模型。在本例中,推理阶段,我们只更新网络$\mathbf{C}$,而网络$\mathbf{\Phi}$和$\mathbf{\Gamma}$则保持不变。需要注意的是,模型的refinement是针对每个batch单独执行的。每当开始一个新的batch,模型的refinement都会从新开始。也就说,当前batch学到的模型不适用于下一个batch,这样以确保灵活的模型自适应性。Fig4(a)展示了自参考误差的降低和模型的收敛。Fig4(b)展示了随着训练轮次(指的是推理阶段的模型更新)的增加,test batch的准确率也在上升。Fig4的结果表明使用测试样本的反馈误差可以提升模型性能,增强模型的泛化能力。

个人理解Fig4中的epoch指的是推理阶段中,网络$\mathbf{C}$训练的轮次。
4.Experiments
4.1.Datasets
使用了两个数据集,MS COCO和CrowdPose。MS COCO数据集是被广泛用于HPE的benchmark,包括64K张图像,共270K个标注的人物实例,每个人物实例标注17个关键点。该数据集包含多种多样的多人姿态,不同的人物大小以及遮挡形式。我们的模型在train2017 split上进行训练,训练集包含57K张图像,共150K个人物实例,在val2017 split上进行了消融实验。CrowdPose数据集包含20K张图像,共计80K个标注的人物实例,每个人物实例标注14个关键点。该数据集包含拥挤人群的场景。在MS COCO数据集上,我们将关键点分为了6组,但是在CrowdPose数据集上,我们将关键点分为了4组。对于CrowdPose数据集,我们在训练集上训练模型,其包含10K张图像,共35.4K个标注的人物实例,在验证集(2K张图像,共8K个人物实例)和测试集(8K张图像,共29K个人物实例)上进行评估。
4.2.Experimental Settings
为了公平的比较,我们使用HRNet和ResNet作为baseline(即用来生成$H_A,H_B,H_C,H_D$等一系列heatmap)。训练配置和之前的工作保持一致。校正网络是一个全卷积网络。训练使用Adam优化器。
4.3.Performance Comparisons


在Fig5中,我们和SCIO的局部搜索进行了比较,我们的方法收敛更快,并且在优化过程中对heatmap的纠正更加准确。
SCIO:Zhehan Kan, Shuoshuo Chen, Zeng Li, and Zhihai He. Self-constrained inference optimization on structural groups for human pose estimation. In ECCV, volume 13665, pages 729–745. Springer, 2022.

4.4.Ablation Studies
我们的方法包含2个重要的创新点,一个是自校正推理(Self-Correctable Inference,SCI),另一个是自适应推理(Self-Adaptable Inference,SAI)。SCI由3个基本部分组成:校正网络、自参考误差、校正网络和FFN的联合训练。

式(5)权重的消融实验:

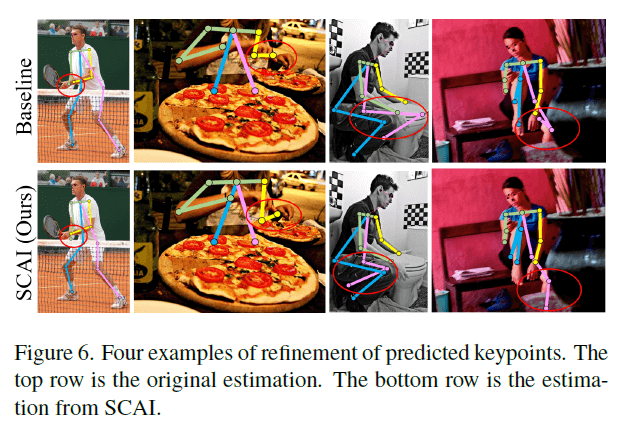
Fig6的4个样本是从COCO val2017数据集中随机抽取的。
在自校正网络的设计中,我们的目标是最小化自参考误差以纠正预测输出。Fig7展示了两个例子,其使用自参考误差作为反馈参考,以引导自校正网络将预测结果拉向自参考误差最小的点。从Fig7可以看出,自参考误差的最小值离GT非常近。

5.Further Discussions and Summary of Unique Contributions
(1)Unique Differences from Related Work.
通过和其他方法(主要是SCIO)比较,突出SCAI的创新性,不再详述。
(2)Algorithm complexity.

SCAI的计算成本有点高。
(3)Summary of contributions.
不再详述。
6.Conclusion
不再详述。
7.Supplemental Material
7.1.More Supporting Results for the Proposed SCAI Method
7.1.1.Further Understanding of Self-Correctable Inference

Fig1(a)中,我们计算了网络$\mathbf{\Phi}$的预测heatmap和GT的$L_2$距离,我们将所有训练样本的距离分布用蓝色实线表示。
FFN(fitness feedback network)的目的是评估纠正后的预测结果$\tilde{H}_D$是否准确。如果$\tilde{H}_D$和GT $H_D$完全一致,那么对应的自参考误差应该达到最小值。在本例中,FFN产生的自参考反馈误差可以成功的将校正过程引向GT。因此,我们用$\parallel \hat{H}_A - H_A^* \parallel$来评估FFN的有效性,在Fig1(a)中用虚线表示。在Fig1(a)中,在训练集上,两个分布曲线的均值基本一样。而在测试集上,网络$\mathbf{\Phi}$的分布曲线相比网络$\mathbf{\Gamma}$明显右移。这说明我们可以用FFN生成的自参考反馈误差来指导预测校正,从而提升泛化能力和预测精度。进一步的描述见Fig1(b)。
7.1.2.Correction Examples of the Prediction Results


Fig3是一个样例的校正过程。当$t=0$时,由于遮挡,原始结果是不正确的。经过SCAI纠正之后,结果变得更加准确。
7.2.Implementation Details
7.2.1.Experimental Settings
评估指标使用OKS(Object Keypoint Similarity):
\[OKS = \frac{\sum_i e^{-d_i^2/2s^2k_i^2} \cdot \delta (v_i > 0)}{\sum_i \delta (v_i > 0)} \tag{7.1}\]对于网络$\mathbf{\Phi}$、网络$\mathbf{C}$和网络$\mathbf{\Gamma}$,我们选择全卷积网络,分别有13层和7层,在实际预测中,我们添加了延迟单元,以等待校正网络所需的反馈误差。网络训练使用Adam优化器。在训练网络$\mathbf{\Phi}$和FFN网络$\mathbf{\Gamma}$时,设batch size=32,初始学习率为0.001,decay rate=0.97。一共训练了210个epoch。对于校正网络$\mathbf{C}$,设batch size=64,初始学习率为0.00041,decay rate=0.97。一共训练了210个epoch,其中$\mathbf{m}$等于120个epoch。权重$a=0.85,b=0.65,\lambda=0.45$。在推理阶段,我们设置batch size=32,最大训练epoch数为20(个人不太理解这里的训练20个epoch指的是什么,在如下推理阶段的伪代码中,并没有找到训练epoch相关内容),初始学习率为0.013,decay rate=0.96。校正迭代次数设置为20。所有实验都是在2块32GB NVIDIA Tesla V100 GPU上进行的。
7.2.2.Details on Training the Prediction Network and the Feedback Fitness Network (FFN)
使用SCIO论文中的方式来进行预训练。Fig4展示了网络$\mathbf{\Phi}$和网络$\mathbf{\Gamma}$的预训练过程。我们将近端关键点的heatmap标记为$\{ H_A,H_B,H_C \}$,将远端关键点的heatmap标记为$H_D$。所有这些heatmap都是由HPE baseline模型生成的,我们使用HRNet作为baseline模型。SCIO一文中提到,在HPE中,远端关键点的精度远低于近端关键点。如Fig4所示,网络$\mathbf{\Phi}$使用近端关键点$\{ H_A,H_B,H_C \}$作为输入,得到对远端关键点$H_D$的预测结果。网络$\mathbf{\Gamma}$使用和$\mathbf{\Phi}$同样的网络结构。它使用$\{H_B,H_C,H_D \}$预测$H_A$。

$\mathbf{\Phi}$和$\mathbf{\Gamma}$在预训练中是联合迭代训练的。Fig4(a)是$\mathbf{\Phi}$的预训练过程,$\mathbf{\Gamma}$是固定的。损失函数为:
\[\mathcal{L}_{\mathbf{\Phi}} = \mathcal{L}_{\mathbf{\Phi}}^0 + \mathcal{L}_{\mathbf{\Phi}}^1 \tag{7.2}\]其中:
\[\mathcal{L}_{\mathbf{\Phi}}^0 = \parallel \hat{H}_D - H_D \parallel_2\] \[\mathcal{L}_{\mathbf{\Phi}}^1 = \parallel \hat{H}_A - H_A \parallel_2\]作者这里用的符号和正文并不统一。$\mathcal{L}_{\mathbf{\Phi}}^0$和$\mathcal{L}_{\mathbf{\Phi}}^1$计算的是预测结果和GT的距离,$H_A,H_D$其实应该标记为$H^*_A,H^*_D$。$\mathbf{\Gamma}$如果使用$H_B,H_C,\hat{H}_D$作为输入,其输出在正文中标记为$\tilde{H_A}$,而这里标记为$\hat{H}_A$。
类似的,如果预训练$\mathbf{\Gamma}$,则固定$\mathbf{\Phi}$。损失函数为:
\[\mathcal{L}_{\mathbf{\Gamma}}=\parallel \hat{H}_A - H_A \parallel_2 + \parallel \hat{H}_D - H_D \parallel_2 \tag{7.3}\]7.2.3.Training Details for the Correction Network and Feedback Fitness Network (FFN)
$\mathbf{\Gamma}$和$\mathbf{C}$是联合训练的。我们首先训练$\mathbf{C}$,然后用更新后的$\tilde{H}_D,\tilde{H}_B,\tilde{H}_C$作为$\mathbf{\Gamma}$的输入来训练$\mathbf{\Gamma}$。训练完成后,$\mathbf{\Gamma}$的输出$\hat{H}_A$作为$\mathbf{C}$的输入来训练$\mathbf{C}$。整个训练过程以迭代的方式进行。迭代训练的原因在于$H_B,H_C,\tilde{H}_D,\hat{H}_A$等输入和GT之间存在的误差会导致$\mathbf{\Gamma}$和$\mathbf{C}$的不准确。通过迭代训练,可以不断优化输入,以提高$\mathbf{\Gamma}$和$\mathbf{C}$的性能。不直接使用GT进行训练的原因在于,以这种方式得到的$\mathbf{\Gamma}$和$\mathbf{C}$可以成功的对baseline模型生成的不正确预测结果进行误差校正。
正如我们在第3.2部分讨论的,和对关键点$X_D$的校正类似,我们也可以用同样的方式来refine关键点$X_B$和$X_C$。唯一的区别在于,校正网络$\mathbf{C}_D$的输入$\hat{H}_D$来自预测网络$\mathbf{\Phi}$,而校正网络$\mathbf{C}_B,\mathbf{C}_C$的输入$H_B,H_C$则直接来自baseline模型,而不是来自$\mathbf{\Phi}$。
7.2.4.Iterative Correction of the Prediction Results
不再详述,详见第7.3部分的伪代码。
7.3.Pseudo Code for the SCAI Algorithm

第6步中用到了$e_s$,但此时$\mathbf{\Gamma}$还没开始进行第一次的预测,所以这个$e_s$是怎么来的呢?个人理解有2种可能,第一,这个$e_s$是随机初始化的,第二,$\mathbf{\Gamma}$用$H_B,H_C,\hat{H}_D$作为输入,输出$\tilde{H}_A$,此时$e_s = H_A - \tilde{H}_A$。
第8步中,使用$E_s$作为损失函数,对$\mathbf{C}_i$进行了一次梯度更新,得到了$\mathbf{C}_i^*$。将第7步计算的$\hat{H}_A$记为$\hat{H}_A^0$,第8步计算得到的$E_s$记为$E_s^0$。
第11步执行完后,需要计算:
\[\hat{H}_A^1 = \mathbf{\Gamma}(H_B,H_C,\tilde{H}_D^0)\] \[E^1_s = \parallel \hat{H}_A^1 - H_A \parallel_2\]上述执行完后,进行第12步,第一次执行循环时,$t=0$,所以先计算$\parallel E_s^1-E_s^0 \parallel$是否大于$\epsilon$,如果大于则进入循环。第13步计算完后,还需要计算:
\[\hat{H}_A^{t+2} = \mathbf{\Gamma}(H_B,H_C,\tilde{H}_D^{t+1})\] \[E^{t+2}_s = \parallel \hat{H}_A^{t+2} - H_A \parallel_2\]以第一次执行循环($t=0$)为例,第13步计算得到$\tilde{H}_D^1$,然后按上式计算$\hat{H}_A^2$和$E_s^2$。然后执行第14步,得到$t=1$,然后判断$\parallel E_s^2 - E_s^1 \parallel$。

第8步使用式(5)作为损失函数,对网络$\mathbf{C}_i$进行一次梯度更新,得到$\mathbf{C}_{i+1}$。注意,此处使用的损失函数是没有$\mathcal{L}_{\mathbf{C}}^1$这一项的,从伪代码中可以看到,这一步损失函数的输入并没有$\hat{H}_A$。
第11步也是对网络$\mathbf{\Gamma}$进行了一次更新。
第16步中的$\tilde{H}_D$是怎么来的呢?个人猜测有两种可能性:1)保存了上一轮训练得到的$\tilde{H}_D$;2)先执行第17步,得到$\bar{H}_A$,然后:
\[\tilde{H}_D = \mathbf{C}_{\mathbf{i+m}}(\hat{H}_D, e_s) \ with \ e_s = H_A - \bar{H_A}\]完事之后继续执行第18步。
第19步使用了完整的式(5)作为损失函数。
8.原文链接
👽Self-Correctable and Adaptable Inference for Generalizable Human Pose Estimation