本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
代码开源地址:Deformable-ConvNets。
视觉识别中的一个关键挑战是如何适应目标在不同尺度、姿态、视角、变形下的几何变换。一般来说,有两种方式。一种是建立足够充分的训练数据集,通常通过数据扩展(比如仿射变换)来实现。另一种是使用具有变换不变性的特征和算法,比如SIFT和滑动窗口机制。
上述方式有两个缺点。第一个缺点,我们会假定几何变换是固定和已知的,用这样的先验知识去扩展数据,并设计特征和算法,但这样会影响到对未知几何变换的泛化。第二个缺点,对于过于复杂的几何变换,手工设计具有变换不变性的特征或算法很困难或根本不可行。
CNN也存在上述两个问题。简言之,CNN对这种大型的、未知的几何变换存在固有的局限性。这源于CNN固定的框架结构:卷积单元在固定位置对输入feature map进行采样(个人注解:以$3 \times 3$卷积为例,卷积操作只考虑到了紧挨着的8个邻居点);池化层以固定比率降低空间分辨率;RoI池化层将RoI划分为特定数量bin等。这种缺乏处理几何变换的内部机制会引起明显的问题。比如,同一CNN层中所有激活单元的感受野大小是相同的,但是不同的位置可能对应不同尺度或变形的目标,因此需要的感受野大小可能也是不同的。另一个例子是针对目标检测任务,几乎所有的方法都依赖基于原始bbox的特征提取,这显然是次优的,尤其是对非刚性目标。
我们提出了两个新的模块,大大提高了CNN对几何变换的建模能力。第一个模块是可变形卷积。它对常规的网格式卷积添加了一个2D偏移,使得网格可自由变形,如Fig1所示。偏移是通过附加的卷积层从前面的feature map中学习到的。

第二个模块是可变形的RoI池化。它将偏移施加在先前划分好的bin上。类似的,这个偏移也是从前面的feature map和RoI中学到的。
这两个模块都是轻量级的,很容易嵌到原有的网络中,也很容易训练。由此产生的CNN称为可变形卷积网络(DCN,deformable convolutional networks或deformable ConvNets)。
2.Deformable Convolutional Networks
CNN中的feature map和卷积都是3D的。可变形卷积和可变形RoI池化都是应用在2D上的,整个操作在通道间保持一致。本部分的描述以2D为准。
2.1.Deformable Convolution
2D卷积包含两步:
- 从输入feature map $\mathbf{x}$中采样一个常规的网格$\mathcal{R}$。
- 加权求和,权重为$\mathbf{w}$。
网格$\mathcal{R}$定义了感受野大小和dilation。比如:
\[\mathcal{R} = \{ (-1,-1),(-1,0), ... , (0,1),(1,1) \}\]定义了一个$3\times 3$的核,dilation为1。
对于输出feature map $\mathbf{y}$中的每个位置$\mathbf{p}_0$,有:
\[\mathbf{y}(\mathbf{p}_0) = \sum_{\mathbf{p}_n \in \mathcal{R}} \mathbf{w}(\mathbf{p}_n) \cdot \mathbf{x} (\mathbf{p}_0 + \mathbf{p}_n) \tag{1}\]在可变形卷积中,我们引入偏移:
\[\{ \Delta \mathbf{p}_n \mid n = 1,...,N \}\]其中,$N = \lvert \mathcal{R} \rvert$。于是,式(1)变为:
\[\mathbf{y}(\mathbf{p}_0) = \sum_{\mathbf{p}_n \in \mathcal{R}} \mathbf{w}(\mathbf{p}_n) \cdot \mathbf{x} (\mathbf{p}_0 + \mathbf{p}_n + \Delta \mathbf{p}_n) \tag{2}\]因为偏移不一定刚好是整数,所以在$\mathbf{x}$上取值时需要用到双线性插值:
\[\mathbf{x} (\mathbf{p}) = \sum_{\mathbf{q}} G (\mathbf{q},\mathbf{p})\cdot \mathbf{x}(\mathbf{q}) \tag{3}\]其中,$\mathbf{p}$是加上偏移后的位置(可能不是整数),即:
\[\mathbf{p} = \mathbf{p}_0 + \mathbf{p}_n + \Delta \mathbf{p}_n\]式(3)中,$\mathbf{q}$是$\mathbf{p}$周围4个整数位置上的点。$G(\cdot , \cdot)$是双线性插值核。$G$包含$x,y$两个维度:
\[G(\mathbf{q}, \mathbf{p}) = g(q_x,p_x) \cdot g(q_y,p_y) \tag{4}\]其中,$g(a,b)=\max (0, 1-\lvert a-b \rvert)$。这里简单解释下式(3)和式(4):

$\mathbf{q}$里面就是$q^{11},q^{12},q^{21},q^{22}$这4个位置,其$x,y$坐标都是整数。根据双线性插值的计算方式,我们可以得到:
\[\mathbf{x}(\mathbf{p}) = \frac{(y_2-y)(x_2-x)}{(y_2-y_1)(x_2-x_1)} \mathbf{x}(q^{11}) + \frac{(y_2-y)(x-x_1)}{(y_2-y_1)(x_2-x_1)} \mathbf{x}(q^{21}) + \frac{(y-y_1)(x_2-x)}{(y_2-y_1)(x_2-x_1)} \mathbf{x}(q^{12}) + \frac{(y-y_1)(x-x_1)}{(y_2-y_1)(x_2-x_1)} \mathbf{x}(q^{22})\]因为$q^{11},q^{12},q^{21},q^{22}$通常都是相邻的像素点,所以有$x_2-x_1 = y_2 - y_1 = 1$,因此上式可简化为:
\[\begin{align}\mathbf{x}(\mathbf{p}) &= (y_2-y)(x_2-x) \mathbf{x}(q^{11}) + (y_2-y)(x-x_1) \mathbf{x}(q^{21}) + (y-y_1)(x_2-x) \mathbf{x}(q^{12}) + (y-y_1)(x-x_1) \mathbf{x}(q^{22}) \\&= G(q^{11},\mathbf{p}) \cdot \mathbf{x}(q^{11}) + G(q^{21},\mathbf{p}) \cdot \mathbf{x}(q^{21}) + G(q^{12},\mathbf{p}) \cdot \mathbf{x}(q^{12}) + G(q^{22},\mathbf{p}) \cdot \mathbf{x}(q^{22}) \\&= \sum_{\mathbf{q}} G(\mathbf{q},\mathbf{p}) \cdot \mathbf{x}(\mathbf{q}) \end{align}\]然后以$G(q^{11},\mathbf{p})$为例,解释下式(4):
\[\begin{align} G(q^{11},\mathbf{p}) &= g(x_1,x) \cdot g(y_1,y) \\&= (1-\lvert x_1-x \rvert) \cdot (1-\lvert y_1-y \rvert) \\&= ((x_2-x_1)-(x-x_1)) \cdot ((y_2-y_1)-(y-y_1))) \\&= (x_2-x)(y_2-y) \end{align}\]
如Fig2所示,偏移是基于同一个输入feature map通过一个卷积层得到的。卷积核和当前卷积层所用卷积核的空间分辨率以及dilation一样(例如,在Fig2中,卷积核都是$3\times 3$大小的,dilation都是1)。输出的偏移场(offset field)大小和输入feature map一样。通道数$2N$表示$N$个2D偏移(如果卷积核大小为$3 \times 3$,那么$N = 3 \times 3$,相当于input feature map上的每个点所用卷积核中的每个权重值都对应一个偏移量)。在训练阶段,同时学习用于产生输出feature map和偏移的卷积核。式(3)和式(4)在反向传播时的梯度计算见附录A。
2.2.Deformable RoI Pooling
很多基于region proposal的目标检测方法都使用了RoI池化。它将任意大小的矩形输入区域转化为固定大小的特征。
个人注解:RoI Pooling的目的是针对输入feature map上任意大小的RoI,都可以提取出固定大小的特征。
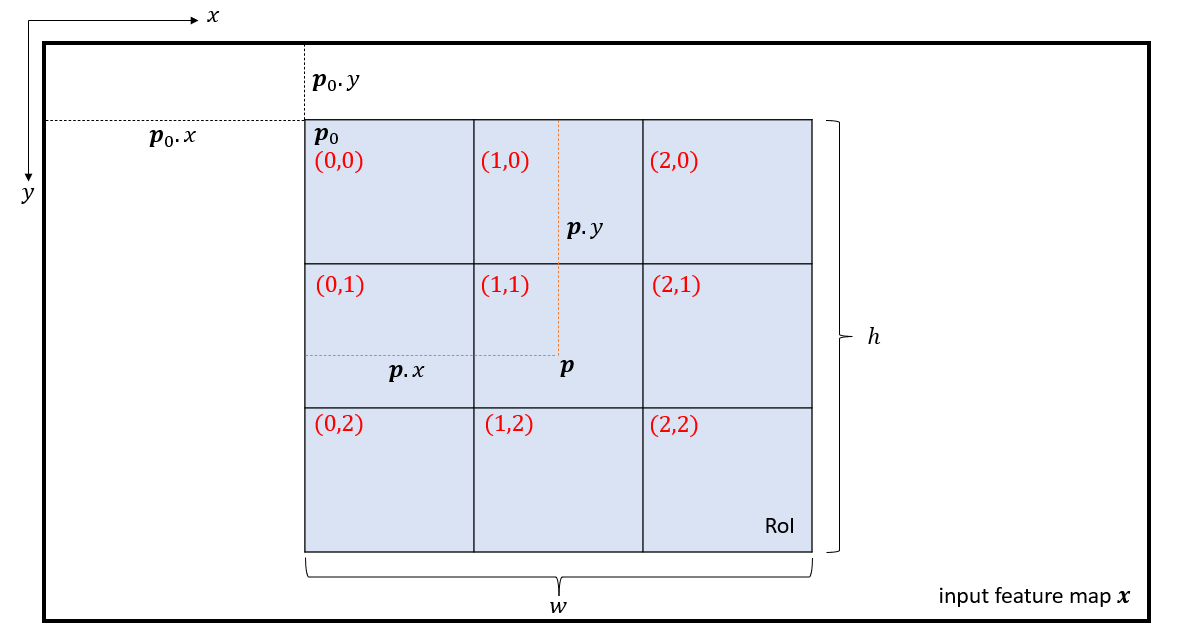
如上图所示,假定输入feature map为$\mathbf{x}$。蓝色区域为RoI,大小为$w \times h$,左上角记为$\mathbf{p}_0$。将RoI划分为$k \times k$个bin,输出$k \times k$大小的feature map $\mathbf{y}$。在上图中,有$k=3$,即一共划分了9个bin,将每个bin记为$(i,j)$(即上图红字,从$(0,0)$到$(2,2)$)。对第$(i,j)$个bin,有:
\[\mathbf{y}(i,j) = \sum_{\mathbf{p} \in bin(i,j)} \mathbf{x}(\mathbf{p}_0 + \mathbf{p}) / n_{ij} \tag{5}\]其中,$n_{ij}$是这个bin里的像素点数量。$\mathbf{p}$为这个bin里的任意一点,即:
\[\lfloor i \frac{w}{k} \rfloor \leqslant p_x < \lceil (i+1) \frac{w}{k} \rceil\] \[\lfloor j \frac{h}{k} \rfloor \leqslant p_y < \lceil (j+1) \frac{h}{k} \rceil\]个人注解:相当于对每个bin进行平均池化。
和式(2)类似,对每个bin施加如下偏移:
\[\{ \Delta \mathbf{p}_{ij} \mid 0 \leqslant i,j < k \}\]因此可得到:
\[\mathbf{y}(i,j) = \sum_{\mathbf{p} \in bin(i,j)} \mathbf{x}(\mathbf{p}_0 + \mathbf{p} + \Delta \mathbf{p}_{ij}) / n_{ij} \tag{6}\]$\Delta \mathbf{p}_{ij}$可能是小数。式(6)也需要双线性插值,见式(3)和式(4)。

Fig3展示了如何获得偏移。首先,RoI pooling(式(5))产生池化后的feature map。接着是一个fc层,产生归一化的偏移$\Delta \hat{\mathbf{p}}_{ij}$。然后对$\Delta \hat{\mathbf{p}}_{ij}$进行转换得到$\Delta \mathbf{p}_{ij}$。转换的方式是和RoI的$w,h$进行element-wise乘法:
\[\Delta \mathbf{p}_{ij} = \gamma \cdot \Delta \hat{\mathbf{p}}_{ij} \circ (w,h)\]个人注解:逐元素相乘的意思就是$\Delta \hat{\mathbf{p}}_{ij}$的$x$值和$w$相乘,$y$值和$h$相乘。
$\gamma$是一个预先设置好的值,用于调节偏移的大小。根据经验,设$\gamma=0.1$。偏移归一化是必要的,其使得偏移的学习不受RoI大小的影响。fc层的反向传播计算见附录A。
👉Position-Sensitive (PS) RoI Pooling

这是全卷积,和RoI pooling不同。通过卷积层,所有的输入feature map都会首先被转换为$k^2(C+1)$个score map,其中,针对每个类别($C$个目标类别+1个背景)都对应$k^2$个score map(对应$k \times k$个bin),如Fig4下所示。偏移的计算如Fig4上所示,对于输入feature map,通过卷积得到$2k^2(C+1)$个offset fields。对每个类别的每个bin来说,对应有2个offset field,通过PS RoI Pooling可以分别得到$x- ,y-$方向的偏移量(也是归一化后的偏移)。将这个偏移量应用在对应的score map上,就能执行deformable PS RoI Pooling了,对每个类别的每个RoI,我们可以得到一个$k \times k$大小的输出。
2.3.Deformable ConvNets
因为可变形卷积和可变形RoI池化都没有修改原有模块的输入和输出大小,所以其可以很容易的替换到原有网络框架中。在训练中,被添加用于学习偏移的卷积层和fc层的权重都被初始化为0。它们的学习率被设置为现有其他层学习率的$\beta$倍(默认$\beta=1$,对于Faster R-CNN中的fc层,设置$\beta=0.01$)。它们通过式(3)和式(4)中的双线性插值运算进行反向传播训练。由此产生的CNN称之为DCN。
为了将DCN应用到SOTA的CNN框架上,我们注意到这些CNN框架通常包括两个阶段。第一个阶段,深度全卷积网络基于整个输入图像生成feature map。第二个阶段,一个特定的下游任务从feature map中生成结果。接下来我们详细阐述这两个阶段。
👉Deformable Convolution for Feature Extraction
我们采用了两个SOTA的特征提取框架:ResNet-101和Inception-ResNet。它们都在ImageNet分类数据集上进行了预训练。
原始的Inception-ResNet被设计用来执行图像识别任务。它存在特征错位(feature misalignment)的问题,无法直接用于密集型预测任务。论文“K. He, X. Zhang, S. Ren, and J. Sun. Aligned-inception-resnet model, unpublished work.”解决了这一问题。修改后的版本称为“Aligned-Inception-ResNet”,详见附录B。
两个模型都包含多个卷积块,一个平均池化和一个1000类别的fc层以用于ImageNet分类任务。我们移除了最后的平均池化和fc层。一个随机初始化的$1\times 1$卷积被添加在最后,将通道数降到1024。和R-FCN一样,我们也将32倍下采样降低到了16倍,即把ResNet-101和Aligned-Inception-ResNet中“conv5”的步长从2改为了1,同样也使用了空洞卷积来弥补降低的步长。
如表1所示,我们尝试将可变形卷积应用在最后几个卷积层(kernel size > 1)上,结果表明修改3个卷积层能在不同任务上得到好的trade-off。
👉Segmentation and Detection Networks
基于上述特征提取框架输出的feature map,我们可以构建一个用于特定任务的网络。
下面,我们用$C$表示目标类别数量。
DeepLab是一个SOTA的语义分割方法。它在feature map之后添加了$1 \times 1$卷积,生成$(C+1)$个map,代表每个像素的类别分数。接下来是一个softmax输出每个像素点的置信度。
Category-Aware RPN基本和Faster R-CNN中的RPN一样,唯一不同的是,Category-Aware RPN输出$(C+1)$个类别,而Faster R-CNN中的RPN只输出两个类别。
Faster R-CNN是一个SOTA的检测器。和原始实现一样,我们将RPN分支添加在conv4 block后。在之前的一些实验中,基于ResNet-101,将RoI pooling层插在conv4和conv5之间,这就给每个RoI留了10层。这种设计可以达到很好的精度,但增加了每个RoI的计算量。因此,我们采用了FPN中的简单设计,将RoI pooling层加在了最后(最后一个$1\times 1$卷积将输出256-D的特征)。在池化后的RoI特征之后,接了两个维度为1024的fc层,再然后是bbox回归分支和分类分支。此外,RoI pooling层也可替换为可变形的RoI池化。
R-FCN是另一个SOTA的检测器。它省掉了每个RoI的计算成本。我们遵循其原始实现。当然,其中的RoI pooling层可替换为可变形的RoI池化。
3.Understanding Deformable ConvNets
当叠加多个可变形卷积时,其影响是深远的,如Fig5所示。
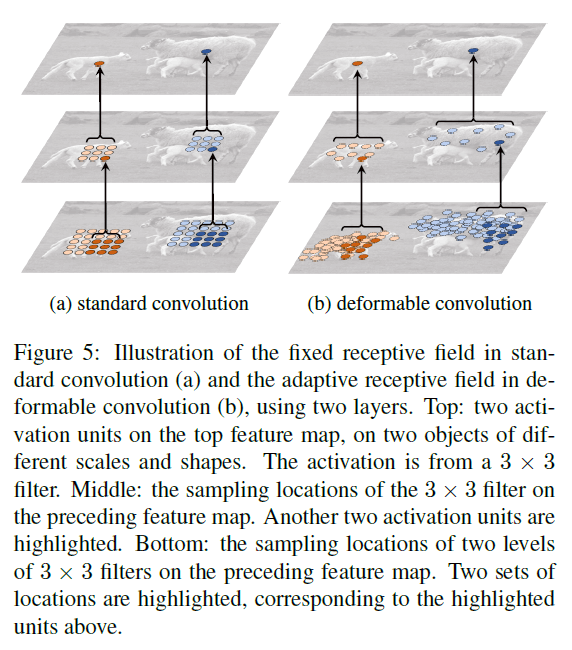
可变形卷积具有一定的自适应性。更多的例子见Fig6。

定量分析见表2。可变形RoI池化的可视化例子见Fig7。

3.1.In Context of RelatedWorks
相关工作,不再详述。
4.Experiments
4.1.Experiment Setup and Implementation
👉Semantic Segmentation
我们使用PASCAL VOC和CityScapes数据集。对于PASCAL VOC,有20个分割类别。我们使用VOC 2012数据集和额外的mask标注。训练集包含10582张图像,验证集有1449张图像。对于CityScapes,训练集有2975张图像,验证集有500张图像。有19个语义类别和一个背景类别。
使用mIoU作为评估指标,mIoU@V表示在PASCAL VOC数据集上,mIoU@C表示在CityScapes数据集上。
在训练和推理阶段,在PASCAL VOC数据集上,将图像短边resize到360个像素,在CityScapes数据集上,将短边resize到1024个像素。图像被随机采样进每个mini-batch中。对于PASCAL VOC,一共迭代了30k次;对于CityScapes,一共迭代了45k次。一共用了8块GPU,每块GPU处理一个batch。迭代的前三分之二,学习率为$10^{-3}$,后三分之一,学习率为$10^{-4}$。
👉Object Detection
使用PASCAL VOC和COCO数据集。对于PASCAL VOC,训练集为VOC 2007 trainval+VOC 2012 trainval。评估使用VOC 2007 test。对于COCO,训练集为trainval,包含120k张图像;测试集为test-dev,包含20k张图像。
使用mAP作为评估指标。对于PASCAL VOC,我们在0.5和0.7两个IoU阈值下计算mAP。对于COCO,我们使用标准的COCO指标:mAP@[0.5:0.95]和mAP@0.5。
在训练和推理阶段,将图像的短边resize到600个像素。图像被随机采样进每个mini-batch中。对于class-aware RPN,每个图像采样了256个RoI。对于Faster R-CNN,采样了256个RoI。对于R-FCN,采样了128个RoI。RoI pooling使用$7 \times 7$个bin。为了加快在VOC上的消融实验,我们遵循FPN,使用预训练好的、固定的RPN来训练Faster R-CNN和R-FCN,之间不再特征共享。与Faster R-CNN中的第一阶段一样,RPN是单独训练的。对于COCO,使用Faster R-CNN中的联合训练,启用特征共享。对于PASCAL VOC,共30k次迭代;对于COCO,共240k次迭代。使用了8块GPU。迭代的前三分之二,学习率为$10^{-3}$,后三分之一,学习率为$10^{-4}$。
4.2.Ablation Study
👉Deformable Convolution

在接下来的实验中,我们使用3层可变形卷积层。
为了更好的理解可变形卷积的机制,我们为可变形卷积核定义了一个有效膨胀(effective dilation),它是卷积核中所有相邻采样位置对之间距离的平均值,这是对卷积核感受野大小的粗略估计。
我们使用表1中的R-FCN,带有3个可变形卷积层,其有效膨胀值的统计结果见表2。

从表2中我们可以得到两点:1)可变形卷积核的感受野大小和目标大小相关,说明变形从图像中得到了有效的学习;2)背景区域的核大小介于中等和大型目标之间,说明较大的感受野对于识别背景区域是必要的。
默认的ResNet-101模型在最后3个卷积层使用了dilation为2的空洞卷积。我们还尝试了4、6、8等不同的dilation值,结果见表3。

👉Deformable RoI Pooling
见表3。
👉Model Complexity and Runtime

4.3.Object Detection on COCO

用到的多尺度:将短边resize到$[480,576,688,864,1200,1400]$。
5.Conclusion
不再赘述。
6.Appendix
6.A.Deformable Convolution/RoI Pooling Backpropagation
式(2)的偏导如下:
\[\begin{align} \frac{\partial \mathbf{y}(\mathbf{p_0})}{\partial \Delta \mathbf{p}_n} &= \sum_{\mathbf{p}_n \in \mathcal{R}} \mathbf{w}(\mathbf{p}_n) \cdot \frac{\partial \mathbf{x}(\mathbf{p}_0 + \mathbf{p}_n + \Delta \mathbf{p}_n)}{\partial \Delta \mathbf{p}_n} \\&= \sum_{\mathbf{p}_n \in \mathcal{R}} \left[ \mathbf{w}(\mathbf{p_n}) \cdot \sum_{\mathbf{q}} \frac{\partial G (\mathbf{q},\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n)}{\partial \Delta \mathbf{p}_n} \mathbf{x}(\mathbf{q}) \right] \end{align} \tag{7}\]其中,$\frac{\partial G (\mathbf{q},\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n)}{\partial \Delta \mathbf{p}_n}$可以从式(4)获得。需要注意的是,偏移量$\Delta \mathbf{p}_n$是2D的,为了简化,我们用$\partial \Delta \mathbf{p}_n$表示$\partial \Delta p_n^x$和$\partial \Delta p_n^y$。
类似的,对于可变形的RoI池化模块,对偏移量$\Delta \mathbf{p}_{ij}$的偏导为:
\[\begin{align} \frac{\partial \mathbf{y}(i,j)}{\partial \Delta \mathbf{p}_{ij}} &= \frac{1}{n_{ij}} \sum_{\mathbf{p} \in bin(i,j)} \frac{\partial \mathbf{x}(\mathbf{p}_0 + \mathbf{p} + \Delta \mathbf{p}_{ij})}{\partial \Delta \mathbf{p}_{ij}} \\&= \frac{1}{n_{ij}} \sum_{\mathbf{p} \in bin (i,j)} \left[ \sum_{\mathbf{q}} \frac{\partial G (\mathbf{q},\mathbf{p}_0 + \mathbf{p} + \Delta \mathbf{p}_{ij})}{\partial \Delta \mathbf{p}_{ij}} \mathbf{x}(\mathbf{q}) \right] \end{align} \tag{8}\]归一化偏移$\Delta \hat{\mathbf{p}}_{ij}$的梯度可以很容易从计算$\Delta \mathbf{p}_{ij} = \gamma \cdot \Delta \hat{\mathbf{p}}_{ij} \circ (w,h)$的导数得到。
6.B.Details of Aligned-Inception-ResNet
在Inception-ResNet中,对于接近输出层的feature map中的cell,其在原始图像上的投影位置和它的感受野中心位置没有对齐。但是下游任务通常会假定二者是对齐的,比如用于语义分割的FCN框架,其利用某个cell的特征来预测原始图像中对应投影位置的像素点标签。
Aligned-Inception-ResNet被提出用于解决这个问题,其结构见表6。
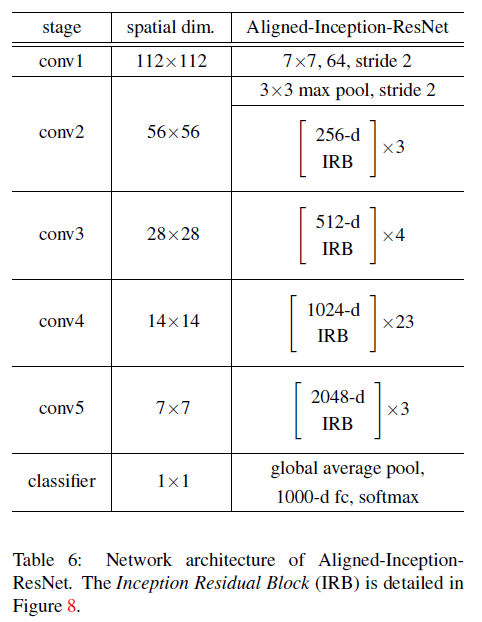
其中,IRB(Inception Residual Block)的结构见Fig8:

通过步长为2的$1\times 1$卷积来改变特征维度。相比Inception-ResNet,Aligned-Inception-ResNet的改动主要有两处:
- 通过在卷积层和池化层进行适当的padding,以解决特征对齐的问题。
- 由重复的模块组成,结构更简单。
Aligned-Inception-ResNet在ImageNet-1K分类任务上进行了预训练。训练遵循ResNet一文。
