本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
SIFT是目前质量最高的图像特征之一,但是其实时性较差。BRISK可以达到与SURF相当的水平,但所需的计算时间却大大减少。BRISK分为两部分:
- Scale-space keypoint detection:尺度空间下的关键点检测。
- Keypoint description:关键点描述。
2.Related Work
不再赘述。
3.BRISK: The Method
3.1.Scale-Space Keypoint Detection
BRISK构建的尺度空间包含$n$个octave,表示为$c_i$。相邻两个octave之间还有一个intra-octave,表示为$d_i$,一共有$n$个intra-octave。其中,$i=\{ 0,1,…,n-1 \}$,通常有$n=4$。每个octave的大小是其下面octave的一半,最底层的$c_0$就是原始图像。每个intra-octave $d_i$位于$c_i$和$c_{i+1}$之间,如Fig1所示。$d_0$是$c_0$的1.5倍下采样。如果用$t$表示尺度,则有$t(c_i)=2^i$和$t(d_i)=2^i \cdot 1.5$。

在每个octave层和每个intra-octave层都使用FAST 9-16检测器来检测关键点,检测器的阈值保持一样,都为$T$。
这里的9-16指的是在FAST算法中,针对某点,如果其圆周16个点中有连续9个点都满足阈值判定,则认为该点为关键点。
然后对这些检测到的关键点进行进一步筛选,即NMS。和SIFT一样,考虑本层以及上下两层,如果其在26邻域内,FAST得分(记为$s$)最高,则保留这一关键点,否则舍弃这一关键点。需要注意的是,$c_0$下面没有intra-octave层了,因此我们构造一个$d_{-1}$作为$c_0$下面的一层,$d_{-1}$就是对原始图像进行一次FAST 5-8检测。
接着需要对关键点进行更细粒度的定位。在关键点所在层及其在上下两层的对应位置,一共3个点,根据其FAST得分拟合出一个抛物线,以确定FAST得分最大的点在哪里(可以通过插值得到),如Fig1右侧所示。注意,refine后得到的关键点所对应的尺度也不再是整数了,而是插值得到的浮点数。
最终的检测效果见Fig2。黄色圆圈的中心表示检测到的关键点,圆圈的大小表示关键点的尺度,圆圈里的线表示关键点的方向。

3.2.Keypoint Description
3.2.1.Sampling Pattern and Rotation Estimation

如Fig3所示,中心点为第3.1部分检测到的关键点,以该关键点为中心,构建不同半径的同心圆,并在每个同心圆上进行一定数目的等间隔采样,如Fig3中蓝色点所示。在Fig3中,包含中心点在内,一共采样了$N=60$个点。
针对每个蓝色点,都以该点为中心执行一次高斯平滑。高斯平滑的标准差与蓝色点所在红色圈的半径成正比。Fig3是$t=1$时的情况($t$的定义见第3.1部分)。
对于关键点$k$,考虑所有采样点之间的两两组合$(\mathbf{p}_i,\mathbf{p}_j)$,一共有$\frac{N\cdot (N-1)}{2}$个点对。采样点$\mathbf{p}_i$经过高斯平滑后的像素值记为$I(\mathbf{p}_i,\sigma_i)$,采样点$\mathbf{p}_j$经过高斯平滑后的像素值记为$I(\mathbf{p}_j,\sigma_j)$,其中,$\sigma_i,\sigma_j$为高斯平滑的标准差。点对$(\mathbf{p}_i,\mathbf{p}_j)$的局部梯度为:
\[\mathbf{g}(\mathbf{p}_i,\mathbf{p}_j) = (\mathbf{p}_j-\mathbf{p}_i) \cdot \frac{I(\mathbf{p}_j,\sigma_j) - I(\mathbf{p}_i,\sigma_i)}{ \| \mathbf{p}_j-\mathbf{p}_i \|^2} \tag{1}\]所有点对的集合为:
\[\mathcal{A} = \{ (\mathbf{p}_i,\mathbf{p}_j) \in \mathbb{R}^2 \times \mathbb{R}^2 \mid i<N \wedge j <i \wedge i,j \in \mathbb{N} \} \tag{2}\]定义短距离点对集合$\mathcal{S}$和长距离点对集合$\mathcal{L}$:
\[\mathcal{S} = \{ (\mathbf{p}_i,\mathbf{p}_j) \in \mathcal{A} \mid \| \mathbf{p}_j-\mathbf{p}_i \| < \delta_{max} \} \subseteq \mathcal{A} \\ \mathcal{L} = \{ (\mathbf{p}_i,\mathbf{p}_j) \in \mathcal{A} \mid \| \mathbf{p}_j-\mathbf{p}_i \| > \delta_{min} \} \subseteq \mathcal{A} \tag{3}\]我们设$\delta_{max} = 9.75t, \delta_{min} = 13.67t$,其中,$t$是关键点$k$对应的尺度(参见第3.1部分)。
关键点$k$的特征方向为:
\[\mathbf{g} = \begin{pmatrix} g_x \\ g_y \end{pmatrix} = \frac{1}{L} \cdot \sum_{(\mathbf{p}_i,\mathbf{p}_j)\in \mathcal{L}} \mathbf{g}(\mathbf{p}_i,\mathbf{p}_j) \tag{4}\]在计算特征方向时只考虑了长距离点对。
3.2.2.Building the Descriptor
为了解决旋转不变性,需要对关键点周围的采样区域旋转至主方向,旋转角度为$\alpha = \text{arctan2}(g_x,g_y)$。通过对所有短距离点对$(\mathbf{p}_i^{\alpha},\mathbf{p}_j^{\alpha})\in \mathcal{S}$的像素值比较来获得关键点的二值描述符$d_k$,其中$\mathbf{p}_i^{\alpha},\mathbf{p}_j^{\alpha}$表示旋转后的采样点。$d_k$中每个值$b$的计算为:
\[b = \begin{cases} 1, & I(\mathbf{p}_j^\alpha, \sigma_j) > I(\mathbf{p}_i^\alpha, \sigma_i) \\ 0, & \text{otherwise} \end{cases} \\ \forall (\mathbf{p}_i^\alpha, \mathbf{p}_j^\alpha) \in \mathcal{S} \tag{5}\]3.3.Descriptor Matching
两个特征描述符之间的距离计算使用汉明距离:即不同的比特位数。
3.4.Notes on Implementation
不再详述。
4.Experiments
评估所用的数据集示例见Fig4:
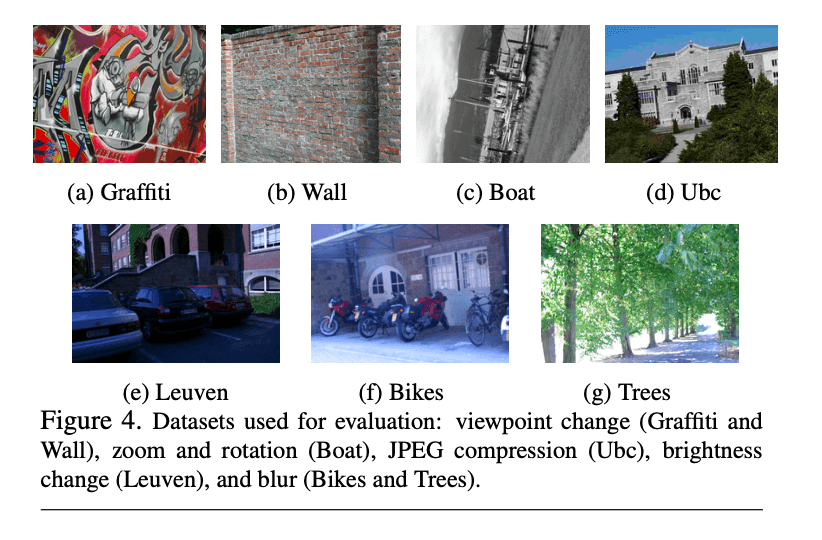
我们将BRISK和SIFT、SURF进行了比较。评估使用了相似性匹配,它认为任何一对关键点,只要它们的描述符距离小于一定阈值,便认为这一对关键点是匹配的。
4.1.BRISK Detector Repeatability
可重复性分数指的是在同一场景中,在不同图像之间成功匹配的关键点的比例(通俗讲就是在不同图像中可以找到同一位置的关键点)。结果对比见Fig5:

从Fig5可以看出,BRISK和SURF的在可重复性上不相上下,但BRISK的计算成本更低。
4.2.Evaluation and Comparison of the Overall BRISK Algorithm

如Fig6所示,BRISK在所有数据集上的表现与SIFT、SURF相当,甚至在某些情况下优于这两者。

Fig7的实验表明,SU-BRISK(S表示single-scale,U表示unrotated)在抵抗小旋转($10^{\circ}$)和尺度变化(10%)方面比BRIEF更具优势。
4.3.Timings
算法耗时的测试只使用了i7 2.67 GHz处理器的一个核。表2是100次实验的平均值。

4.4.An Example

5.Conclusions
6.原文链接
👽BRISK:Binary Robust invariant scalable keypoints