【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.半监督聚类
聚类是一种典型的无监督学习任务,然而在现实聚类任务中我们往往能获得一些额外的监督信息,于是可通过半监督聚类(semi-supervised clustering)来利用监督信息以获得更好的聚类效果。
聚类任务中获得的监督信息大致有两种类型。第一种类型是“必连”(must-link)与“勿连”(cannot-link)约束,前者是指样本必属于同一个簇,后者是指样本必不属于同一个簇;第二种类型的监督信息则是少量的有标记样本。
约束$k$均值(Constrained k-means)算法是利用第一类监督信息的代表。给定样本集$D = \{ \mathbf{x}_1,\mathbf{x}_2, …, \mathbf{x}_m \}$以及“必连”关系集合$\mathcal{M}$和“勿连”关系集合$\mathcal{C}$,$(\mathbf{x}_i,\mathbf{x}_j) \in \mathcal{M}$表示$\mathbf{x}_i$与$\mathbf{x}_j$必属于同簇,$(\mathbf{x}_i,\mathbf{x}_j) \in \mathcal{C}$表示$\mathbf{x}_i$与$\mathbf{x}_j$必不属于同簇。该算法是k均值算法的扩展,它在聚类过程中要确保$\mathcal{M}$与$\mathcal{C}$中的约束得以满足,否则将返回错误提示,算法如图13.7所示。

以如下数据集为例:
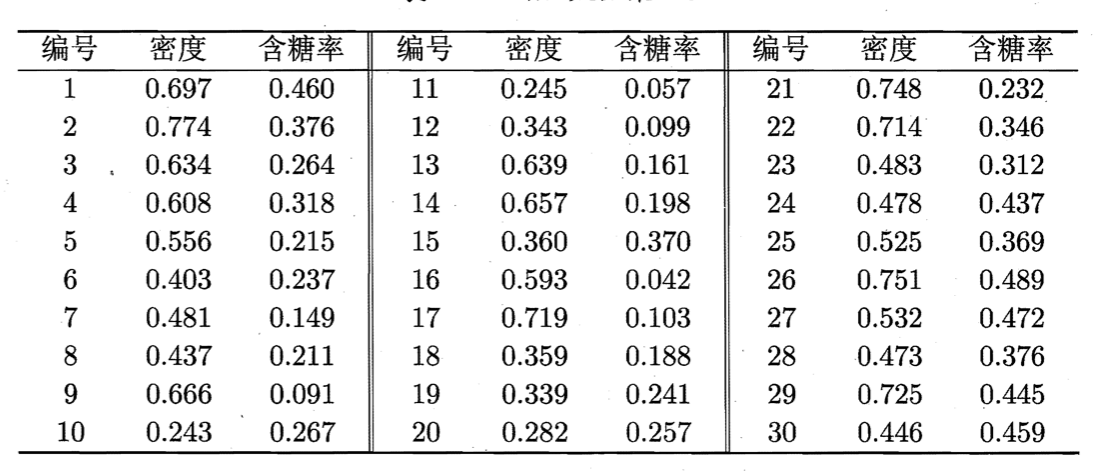
令样本$\mathbf{x}_4$与$\mathbf{x}_{25}$,$\mathbf{x}_{12}$与$\mathbf{x}_{20}$,$\mathbf{x}_{14}$与$\mathbf{x}_{17}$之间存在必连约束,$\mathbf{x}_2$与$\mathbf{x}_{21}$,$\mathbf{x}_{13}$与$\mathbf{x}_{23}$,$\mathbf{x}_{19}$与$\mathbf{x}_{23}$之间存在勿连约束,即:
\[\mathcal{M} = \{ (\mathbf{x}_4,\mathbf{x}_{25}),(\mathbf{x}_{25},\mathbf{x}_4),(\mathbf{x}_{12},\mathbf{x}_{20}),(\mathbf{x}_{20},\mathbf{x}_{12}),(\mathbf{x}_{14},\mathbf{x}_{17}),(\mathbf{x}_{17},\mathbf{x}_{14}) \}\] \[\mathcal{C} = \{ (\mathbf{x}_2,\mathbf{x}_{21}),(\mathbf{x}_{21},\mathbf{x}_2),(\mathbf{x}_{13},\mathbf{x}_{23}),(\mathbf{x}_{23},\mathbf{x}_{13}),(\mathbf{x}_{19},\mathbf{x}_{23}),(\mathbf{x}_{23},\mathbf{x}_{19}) \}\]
设聚类簇数$k=3$,随机选取样本$\mathbf{x}_6,\mathbf{x}_{12},\mathbf{x}_{27}$作为初始均值向量,图13.8显示出约束k均值算法在不同迭代轮数后的聚类结果。经5轮迭代后均值向量不再发生变化(与第4轮迭代相同),于是得到最终聚类结果:
\[C_1 = \{ \mathbf{x}_3,\mathbf{x}_5,\mathbf{x}_7,\mathbf{x}_9,\mathbf{x}_{13},\mathbf{x}_{14},\mathbf{x}_{16},\mathbf{x}_{17},\mathbf{x}_{21} \}\] \[C_2 = \{ \mathbf{x}_6,\mathbf{x}_8,\mathbf{x}_{10},\mathbf{x}_{11},\mathbf{x}_{12},\mathbf{x}_{15},\mathbf{x}_{18},\mathbf{x}_{19},\mathbf{x}_{20} \}\] \[C_3 = \{ \mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_4,\mathbf{x}_{22},\mathbf{x}_{23},\mathbf{x}_{24},\mathbf{x}_{25},\mathbf{x}_{26},\mathbf{x}_{27},\mathbf{x}_{28},\mathbf{x}_{29},\mathbf{x}_{30} \}\]第二种监督信息是少量有标记样本。给定样本集$D = \{ \mathbf{x}_1,\mathbf{x}_2,…,\mathbf{x}_m \}$,假定少量的有标记样本为$S = \cup_{j=1}^k S_j \subset D$,其中$S_j \neq \varnothing$为隶属于第$j$个聚类簇的样本。这样的监督信息利用起来很容易:直接将它们作为“种子”,用它们初始化$k$均值算法的$k$个聚类中心,并且在聚类簇迭代更新过程中不改变种子样本的簇隶属关系。这样就得到了约束种子$k$均值(Constrained Seed k-means)算法,其算法描述如图13.9所示。
此处样本标记指簇标记(cluster label),不是类别标记(class label)。

仍以之前的数据集为例,假定作为种子的有标记样本为:
\[S_1 = \{ \mathbf{x}_4,\mathbf{x}_{25} \}, S_2 = \{ \mathbf{x}_{12},\mathbf{x}_{20} \}, S_3 = \{ \mathbf{x}_{14},\mathbf{x}_{17} \}\]以这三组种子样本的平均向量作为初始均值向量,图13.10显示出约束种子$k$均值算法在不同迭代轮数后的聚类结果。经4轮迭代后均值向量不再发生变化(与第3轮迭代相同),于是得到最终聚类结果:
\[C_1 = \{ \mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_4,\mathbf{x}_{22},\mathbf{x}_{23},\mathbf{x}_{24},\mathbf{x}_{25},\mathbf{x}_{26},\mathbf{x}_{27},\mathbf{x}_{28},\mathbf{x}_{29},\mathbf{x}_{30} \}\] \[C_2 = \{ \mathbf{x}_6,\mathbf{x}_7,\mathbf{x}_8,\mathbf{x}_{10},\mathbf{x}_{11},\mathbf{x}_{12},\mathbf{x}_{15},\mathbf{x}_{18},\mathbf{x}_{19},\mathbf{x}_{20} \}\] \[C_3 = \{ \mathbf{x}_3,\mathbf{x}_5,\mathbf{x}_9,\mathbf{x}_{13},\mathbf{x}_{14},\mathbf{x}_{16},\mathbf{x}_{17},\mathbf{x}_{21} \}\]