本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
根据以往的研究工作,提高深度卷积神经网络性能的策略分为两个方面:
- 如何组合特征并将其传播到后续层。
- 如何使梯度更高效地传播到所有层。
我们提出一个新的角度:在训练过程中,如何组合各层的梯度以获得更好的学习效果。因此,我们提出了PRN(partial residual networks)的概念,将残差连接转换为一个用于梯度组合的路径。由于PRN的设计策略不再是传播特征组合,而是传播梯度组合,因此它更适合轻量级网络。这主要是因为特征组合会产生新的层,而梯度组合则不会。正因为PRN具备轻量化的特点,它也能有效应用于嵌入式设备的实时推理场景。
我们选择目标检测任务来验证PRN的性能,并证明它在轻量化模型中同样表现出色。PRN有如下优势:
- PRN使浅层网络也能学习到丰富的信息。
- PRN可以将通道数不同的层进行组合,因此在网络结构设计上具有极强的灵活性。
- PRN的推理过程占用资源极少,适合部署在资源受限的嵌入式系统中。
- PRN在通道维度进行稀疏化,因此更适用于浅层网络架构。
- PRN的运行速度非常快,非常适合对实时处理有要求的任务。
2.Partial Residual Networks
PRN是由一系列部分残差连接块组成的。部分残差连接的结构见Fig1。

第$l$层的feature map的通道数为$c_2$,第$l-k$层的feature map的通道数为$c_1$,且有$c \leqslant c_1$和$c \leqslant c_2$。简单来说,ResNet是基于所有通道做的残差连接,而PRN则是基于部分通道做的残差连接。Fig1可用如下公式表示:
\[x_l = [ H_l(x_{l-1})_{[0:c-1]} + {x_{l-k}}_{[0:c-1]}, H_l(x_{l-1})_{[c:c_l]} ] \tag{1}\]其中,$x_l$表示第$l$层输出的feature map,$H_l$表示第$l$层的非线性转换函数,$[a,b,…]$表示将$a,b,…$concat在一起,$[a:b]=[a,a+1,…b]$表示从通道$a$到通道$b$的feature map。当$c=0$时,式(1)变为$x_l = H_l (x_{l-1})$,也就是最普通的神经网络。当$c=c_1=c_2$时,式(1)变为$x_l = H_l (x_{l-1}) + x_{l-k}$,也就是ResNet。
PRN的3种框架:
第一种框架结构见Fig2,各层的通道数都是一样的,设置稀疏比率$\rho$来进行稀疏残差连接。

第二种框架结构见Fig3,通道数逐层线性递减,从$c$递减到$\gamma \times c$,递减率为$\gamma$。

第三种框架结构见Fig4,每层的通道数可以不一致,残差连接的路径也可长可短。

3.Combination of Gradients
梯度传播主要由两部分组成:一是梯度的来源,另一个是梯度的时间戳。我们用$G_t^s$表示梯度,其中$s$表示来源,$t$表示时间戳。我们将分别使用时间戳和来源来观察训练过程中梯度是如何组合的。此外,我们还将解释为何ResNet、ResNext、DenseNet、SparseNet以及PRN能够基于梯度的组合更有效地进行学习。
3.1.Timestamp
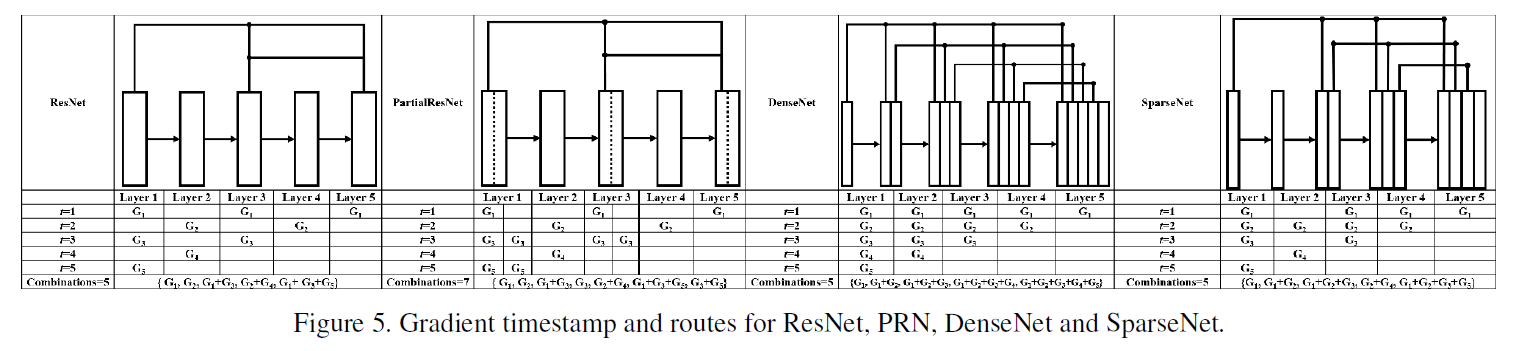
Fig5展示的都是5层的网络。我们以ResNet为例解释一下这个图,在这个5层的ResNet中,梯度反向传播的流如下所示:

$t$表示时间戳。
- 当$t=1$时,第5、3、1层的参数可以得到更新;
- 当$t=2$时,第4、2层的参数可以得到更新;
- 当$t=3$时,第3、1层的参数可以得到更新;
- 当$t=4$时,只有第2层的参数可以得到更新;
- 当$t=5$时,只有第1层的参数可以得到更新。
对于每层的梯度:
- 对于第5层来说,梯度信息来自$\{G_1 \}$;
- 对于第4层来说,梯度信息来自$\{G_2 \}$;
- 对于第3层来说,梯度信息来自$\{ G_1 + G_3 \}$;
- 对于第2层来说,梯度信息来自$\{ G_2 + G_4 \}$;
- 对于第1层来说,梯度信息来自$\{ G_1 + G_3 + G_5 \}$。
所以一共是有5种梯度组合:
\[\{ G_1,G_2,G_1+G_3,G_2+G_4,G_1+G_3+G_5 \}\]如Fig5所示,相比ResNet、DenseNet和SparseNet,PRN的梯度组合更丰富。
3.2.Source
Fig6是$G_{t=1}^s$的梯度来源示意图,最左侧是ResNet,中间是PRN,最右侧是DenseNet。

针对ResNet框架,其将完全相同的梯度传播到所有目标层,这也解释了为什么ResNet容易学到大量冗余信息。为了解决这个问题,PRN将一部分梯度进行分离,从而产生更丰富的梯度组合。
3.3.Summary
- 对于ResNet,不同的层共享大量来自相同时间戳和相同来源的梯度。
- 对于DenseNet,其传播来自不同来源,但具有相同时间戳的梯度,这也解释了为什么DenseNet能够避免像ResNet那样学习到大量冗余信息的问题。
- SparseNet所采用的稀疏连接策略将梯度时间戳分配到不同的层上,这种方式减少了梯度的来源,但增加了时间戳的变化次数,同时也降低了计算量。
- PRN在通道维度上进行了部分残差连接,这种方式在不增加网络层数的情况下提升了梯度在时间戳维度上的组合数。同时,它也对梯度来源进行了分流,增加了梯度来源的多样性。
4.Experimental Results
4.1.Experimental setting
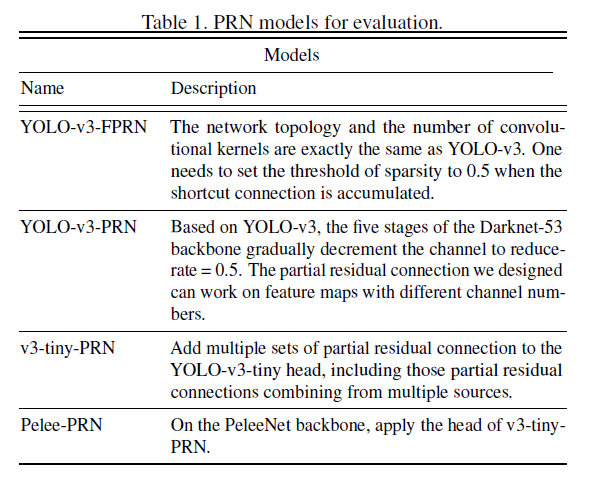
我们评估了4种不同的PRN模型:
YOLO-v3、YOLO-v3-FPRN、YOLO-v3-PRN的backbone分别见Fig7(a)、Fig7(b)、Fig7(c):

在Darknet53的基础上,Darknet53-FPRN只是将残差连接替换为了50%通道的部分残差连接。鉴于PRN可以应用在不同通道数的层上,所以Darknet53-PRN在Darknet53-FPRN的基础上,在每个block内,将通道数做了线性递减处理。
v3-tiny-PRN是在YOLO-v3-tiny的head中添加了部分残差连接。而Pelee-PRN则是在PeleeNet backbone的基础上,应用了v3-tiny-PRN的head。tiny PRN head的框架见Fig8(吐槽一下,这篇论文的配图都好不清晰,根本看不清楚):

4.2.Analysis on effect of combination of gradient
我们设计了多种PRN架构,这些架构利用了不同丰富程度的梯度组合。我们的目的是为了验证:当我们尝试降低模型的计算复杂度时,如果采用最大化梯度组合利用率的策略,是否能够获得最大的性能收益。我们在ILSVRC 2012所用的ImageNet验证集上对实验结果进行了验证。同时,我们也分析了参数$\gamma$(用于控制计算量)对测试结果的影响。
我们将Fig3中的PRN架构称为PRN-shrink。对于一个k层的PRN-shrink,梯度时间戳组合的总数和梯度来源的总数都是:
\[1+2+...+k=\frac{(1+k)\times k}{2}\]
我们将Fig9中的PRN架构称为PRN-expand。对于一个k层的PRN-expand,梯度时间戳组合的总数为:
\[1+1+...+1=k\]梯度来源的总数为:
\[1+2+...+k=\frac{(1+k)\times k}{2}\]
我们将Fig10中的PRN架构称为PRN-bottleneck。对于一个k层的PRN-bottleneck,梯度时间戳组合的总数为:
\[\frac{(1+k/2)\times (k/2)}{2}+(k/2) = \frac{(1+k/2)\times (k/2)+k}{2}\]介于PRN-shrink和PRN-expand之间。梯度来源的总数为:
\[1+2+...+(k/2)+(k/2)+((k/2)-1)+...+1=2\times \frac{(1+k/2)\times (k/2)}{2} = (1+k/2)\times (k/2)\]大概是PRN-shrink和PRN-expand的一半左右。所以对于梯度时间戳组合的总数,有:
\[\text{PRN-expand} < \text{PRN-bottleneck} < \text{PRN-shrink}\]对于梯度来源的总数,有:
\[\text{PRN-bottleneck} < \text{PRN-expand} = \text{PRN-shrink}\]测试结果见Fig11:

在Fig11中,$\gamma$分别被设置为0.5和0.75,具体准确率值为:
| Top-1 Accuracy | $\gamma = 0.75$ | $\gamma=0.5$ |
|---|---|---|
| PRN-shrink | 76.8% | 76.4% |
| PRN-expand | 75.7% | 72.7% |
| PRN-bottleneck | 75.5% | 72.7% |
可以得到以下结论:
- PRN-shrink效果最佳。
- 通过比较PRN-expand和PRN-bottleneck的实验结果可以看出,相较于增加梯度时间戳组合,增加梯度来源组合的收益更大。
- $\gamma$越低,准确率越低。
4.3.Comparison with GPU-based real-time models

相比YOLO-v3,YOLO-v3-FPRN的精度略有提升,而YOLO-v3-PRN在精度基本持平的情况下,减少了35%的计算量,并将推理速度提升了一倍。
4.4.Comparison with state-of-the-art lightweight models

4.5.Applications in the real world
我们基于PRN架构训练的目标检测模型,已在多个国家与交通运输部合作,建立了实时交通流分析平台。
Fig12展示了部署在路口的智能交通流分析机箱,该设备内置我们开发的嵌入式计算装置和用于视频存储的1TB SSD。

Fig13展示了部署在路口的,基于鱼眼镜头的交通分析系统,该系统可用于分析车辆类型、车身颜色、车速以及转向车流。

Fig14展示了交通跟踪系统,可用于分析即时车速、车辆排队长度等交通信息。

Fig15展示了道路车牌识别系统。该系统不仅能够检测和跟踪车辆,还可以识别车牌号码。

5.Conclusions
不再赘述。
6.原文链接
👽Enriching Variety of Layer-wise Learning Information by Gradient Combination