【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.隐马尔可夫模型
机器学习最重要的任务,是根据一些已观察到的证据(例如训练样本)来对感兴趣的未知变量(例如类别标记)进行估计和推测。概率模型(probabilistic model)提供了一种描述框架,将学习任务归结于计算变量的概率分布。在概率模型中,利用已知变量推测未知变量的分布称为“推断”(inference),其核心是如何基于可观测变量推测出未知变量的条件分布。具体来说,假定所关心的变量集合为$Y$,可观测变量集合为$O$,其他变量的集合为$R$,“生成式”(generative)模型考虑联合分布$P(Y,R,O)$,“判别式”(discriminative)模型考虑条件分布$P(Y,R \mid O)$。给定一组观测变量值,推断就是要由$P(Y,R,O)$或$P(Y,R \mid O)$得到条件概率分布$P(Y \mid O)$。
基于学习器进行预测,例如根据纹理、颜色、根蒂等信息判断一个瓜是否为好瓜就是在做推断;但推断远超出预测范畴,例如在吃到一个不见根蒂的好瓜时,“由果溯因”逆推其根蒂的状态也是推断。
直接利用概率求和规则消去变量$R$显然不可行,因为即便每个变量仅有两种取值的简单问题,其复杂度已至少是$O(2^{\lvert Y \rvert + \lvert R \rvert})$。另一方面,属性变量之间往往存在复杂的联系,因此概率模型的学习,即基于训练样本来估计变量分布的参数往往相当困难。为了便于研究高效的推断和学习算法,需有一套能简洁紧凑地表达变量间关系的工具。
概率图模型(probabilistic graphical model)是一类用图来表达变量相关关系的概率模型。它以图为表示工具,最常见的是用一个结点表示一个或一组随机变量,结点之间的边表示变量间的概率相关关系,即“变量关系图”。根据边的性质不同,概率图模型可大致分为两类:第一类是使用有向无环图表示变量间的依赖关系,称为有向图模型或贝叶斯网(Bayesian network);第二类是使用无向图表示变量间的相关关系,称为无向图模型或马尔可夫网(Markov network)。
若变量间存在显式的因果关系,则常使用贝叶斯网;若变量间存在相关性,但难以获得显式的因果关系,则常使用马尔可夫网。
隐马尔可夫模型(Hidden Markov Model,简称HMM)是结构最简单的动态贝叶斯网(dynamic Bayesian network),这是一种著名的有向图模型,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
静态贝叶斯网参见:【机器学习基础】第二十五课:贝叶斯网。
如图14.1所示,隐马尔可夫模型中的变量可分为两组。第一组是状态变量$\{ y_1,y_2,…,y_n \}$,其中$y_i \in \mathcal{Y}$表示第$i$时刻的系统状态。通常假定状态变量是隐藏的、不可被观测的,因此状态变量亦称隐变量(hidden variable)。第二组是观测变量$\{ x_1,x_2,…,x_n \}$,其中$x_i \in \mathcal{X}$表示第$i$时刻的观测值。在隐马尔可夫模型中,系统通常在多个状态$\{ s_1,s_2,…,s_N \}$之间转换,因此状态变量$y_i$的取值范围$\mathcal{Y}$(称为状态空间)通常是有$N$个可能取值的离散空间。观测变量$x_i$可以是离散型也可以是连续型,为便于讨论,我们仅考虑离散型观测变量,并假定其取值范围$\mathcal{X}$为$\{ o_1,o_2,…,o_M \}$。
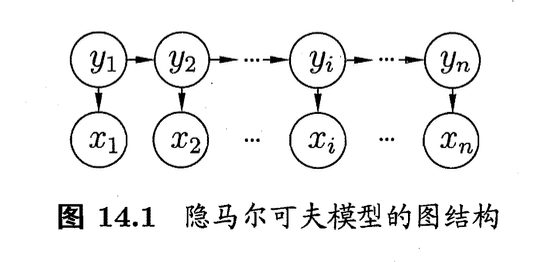
图14.1中的箭头表示了变量间的依赖关系。在任一时刻,观测变量的取值仅依赖于状态变量,即$x_t$由$y_t$确定,与其他状态变量及观测变量的取值无关。同时,$t$时刻的状态$y_t$仅依赖于$t-1$时刻的状态$y_{t-1}$,与其余$n-2$个状态无关。这就是所谓的“马尔可夫链”(Markov chain),即:系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。基于这种依赖关系,所有变量的联合概率分布为:
\[P(x_1,y_1,...,x_n,y_n) = P(y_1)P(x_1 \mid y_1) \prod _{i=2}^n P(y_i \mid y_{i-1}) P(x_i \mid y_i) \tag{1}\]除了结构信息,欲确定一个隐马尔可夫模型还需以下三组参数:
-
状态转移概率:模型在各个状态间转换的概率,通常记为矩阵$\mathbf{A} = [a_{ij}]_{N \times N}$,其中:
\[a_{ij} = P(y_{t+1} = s_j \mid y_t = s_i), \quad 1 \leqslant i,j \leqslant N\]表示在任意时刻$t$,若状态为$s_i$,则在下一时刻状态为$s_j$的概率。
-
输出观测概率:模型根据当前状态获得各个观测值的概率,通常记为矩阵$\mathbf{B} = [b_{ij}]_{N \times M}$,其中:
\[b_{ij}=P(x_t=o_j \mid y_t=s_i), \quad 1 \leqslant i \leqslant N, 1\leqslant j \leqslant M\]表示在任意时刻$t$,若状态为$s_i$,则观测值$o_j$被获取的概率。
-
初始状态概率:模型在初始时刻各状态出现的概率,通常记为$\mathbf{\pi} = (\pi_1,\pi_2,…,\pi_N)$,其中:
\[\pi_i = P(y_1=s_i), \quad 1 \leqslant i \leqslant N\]表示模型的初始状态为$s_i$的概率。
通过指定状态空间$\mathcal{Y}$、观测空间$\mathcal{X}$和上述三组参数,就能确定一个隐马尔可夫模型,通常用其参数$\lambda = [\mathbf{A},\mathbf{B},\mathbf{\pi}]$来指代。给定隐马尔可夫模型$\lambda$,它按如下过程产生观测序列$\{ x_1,x_2,…,x_n \}$:
- 设置$t=1$,并根据初始状态概率$\mathbf{\pi}$选择初始状态$y_1$;
- 根据状态$y_t$和输出观测概率$\mathbf{B}$选择观测变量取值$x_t$;
- 根据状态$y_t$和状态转移矩阵$\mathbf{A}$转移模型状态,即确定$y_{t+1}$;
- 若$t<n$,设置$t=t+1$,并转到第2步,否则停止。
其中$y_t \in \{ s_1,s_2,…,s_N \}$和$x_t \in \{ o_1,o_2,…,o_M \}$分别为第$t$时刻的状态和观测值。
在实际应用中,人们常关注隐马尔可夫模型的三个基本问题:
- 给定模型$\lambda = [\mathbf{A},\mathbf{B},\mathbf{\pi}]$,如何有效计算其产生观测序列$\mathbf{x}= \{ x_1,x_2,…,x_n \}$的概率$P(\mathbf{x} \mid \lambda)$?换言之,如何评估模型与观测序列之间的匹配程度?
- 给定模型$\lambda = [\mathbf{A},\mathbf{B},\mathbf{\pi}]$和观测序列$\mathbf{x}=\{x_1,x_2,…,x_n \}$,如何找到与此观测序列最匹配的状态序列$\mathbf{y}=\{ y_1,y_2,…,y_n\}$?换言之,如何根据观测序列推断出隐藏的模型状态?
- 给定观测序列$\mathbf{x}=\{x_1,x_2,…,x_n \}$,如何调整模型参数$\lambda=[\mathbf{A},\mathbf{B},\mathbf{\pi}]$使得该序列出现的概率$P(\mathbf{x}\mid \lambda )$最大?换言之,如何训练模型使其能最好地描述观测数据?
上述问题在现实应用中非常重要。例如许多任务需根据以往的观测序列$\{x_1,x_2,…,x_{n-1}\}$来推测当前时刻最有可能的观测值$x_n$,这显然可转化为求取概率$P(\mathbf{x}\mid \lambda)$,即上述第一个问题;在语音识别等任务中,观测值为语音信号,隐藏状态为文字,目标就是根据观测信号来推断最有可能的状态序列(即对应的文字),即上述第二个问题;在大多数现实应用中,人工指定模型参数已变得越来越不可行,如何根据训练样本学得最优的模型参数,恰是上述第三个问题。值得庆幸的是,基于式(1)的条件独立性,隐马尔可夫模型的这三个问题均能被高效求解。