【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.条件随机场
条件随机场(Conditional Random Field,简称CRF)是一种判别式无向图模型。【机器学习基础】第六十二课:[概率图模型]隐马尔可夫模型中提到过,生成式模型是直接对联合分布进行建模,而判别式模型则是对条件分布进行建模。之前介绍的隐马尔可夫模型和马尔可夫随机场都是生成式模型,而条件随机场则是判别式模型。
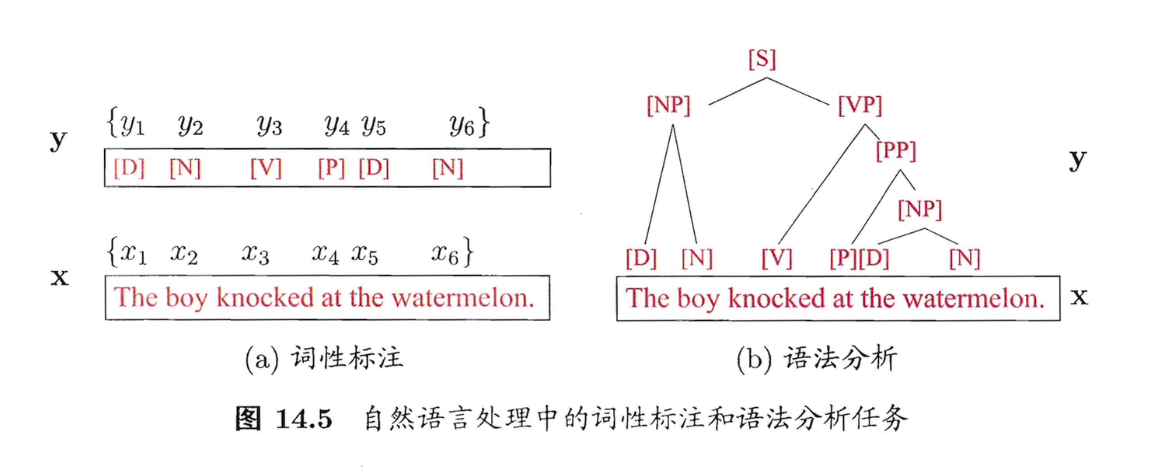
条件随机场试图对多个变量在给定观测值后的条件概率进行建模。具体来说,若令$\mathbf{x}=\{x_1,x_2,…,x_n \}$为观测序列,$\mathbf{y}=\{y_1,y_2,…,y_n \}$为与之相应的标记序列,则条件随机场的目标是构建条件概率模型$P(\mathbf{y}\mid \mathbf{x})$。需注意的是,标记变量$\mathbf{y}$可以是结构型变量,即其分量之间具有某种相关性。例如在自然语言处理的词性标注任务中,观测数据为语句(即单词序列),标记为相应的词性序列,具有线性序列结构,如图14.5(a)所示;在语法分析任务中,输出标记则是语法树,具有树形结构,如图14.5(b)所示。
令$G=\langle V,E \rangle$表示结点与标记变量$\mathbf{y}$中元素一一对应的无向图,$y_v$表示与结点$v$对应的标记变量,$n(v)$表示结点$v$的邻接结点,若图$G$的每个变量$y_v$都满足马尔可夫性,即:
\[P(y_v \mid \mathbf{x},\mathbf{y}_{V\backslash \{v\}}) = P(y_v \mid \mathbf{x},\mathbf{y}_{n(v)}) \tag{1}\]则$(\mathbf{y},\mathbf{x})$构成一个条件随机场。
理论上来说,图$G$可具有任意结构,只要能表示标记变量之间的条件独立性关系即可。但在现实应用中,尤其是对标记序列建模时,最常用的仍是图14.6所示的链式结构,即“链式条件随机场”(chain-structured CRF)。下面我们主要讨论这种条件随机场。
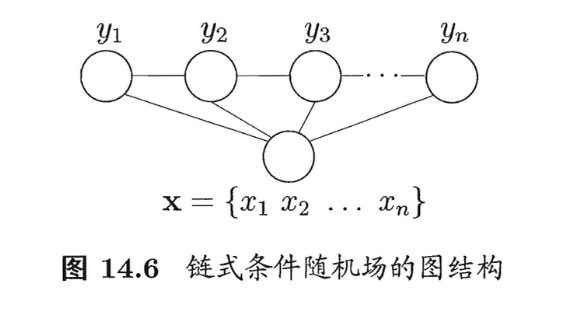
与马尔可夫随机场定义联合概率的方式类似,条件随机场使用势函数和图结构上的团来定义条件概率$P(\mathbf{y}\mid \mathbf{x})$。给定观测序列$\mathbf{x}$,图14.6所示的链式条件随机场主要包含两种关于标记变量的团,即单个标记变量$\{y_i\}$以及相邻的标记变量$\{ y_{i-1},y_i \}$。选择合适的势函数,即可得到形如“【机器学习基础】第六十三课:[概率图模型]马尔可夫随机场”中式(1)的条件概率定义。在条件随机场中,通过选用指数势函数并引入特征函数(feature function),条件概率被定义为:
\[P(\mathbf{y}\mid \mathbf{x})=\frac{1}{Z}\exp \left( \sum_j \sum_{i=1}^{n-1} \lambda_j t_j (y_{i+1},y_i,\mathbf{x},i) + \sum_k \sum_{i=1}^n \mu_k s_k (y_i,\mathbf{x},i) \right) \tag{2}\]其中$t_j(y_{i+1},y_i,\mathbf{x},i)$是定义在观测序列的两个相邻标记位置上的转移特征函数(transition feature function),用于刻画相邻标记变量之间的相关关系以及观测序列对它们的影响,$s_k(y_i,\mathbf{x},i)$是定义在观测序列的标记位置$i$上的状态特征函数(status feature function),用于刻画观测序列对标记变量的影响,$\lambda_j$和$\mu_k$为参数,$Z$为规范化因子,用于确保式(2)是正确定义的概率。
显然,要使用条件随机场,还需定义合适的特征函数。特征函数通常是实值函数,以刻画数据的一些很可能成立或期望成立的经验特性。以图14.5(a)的词性标注任务为例,若采用转移特征函数:
\[t_j (y_{i+1},y_i,\mathbf{x},i) = \begin{cases} 1, \ \text{if } y_{i+1}=[P],y_i=[V] \text{ and } x_i = "knock"; \\ 0, \ \text{otherwise,} \end{cases}\]则表示第$i$个观测值$x_i$为单词”knock”时,相应的标记$y_i$和$y_{i+1}$很可能分别为$[V]$和$[P]$。若采用状态特征函数:
\[s_k(y_i,\mathbf{x},i)=\begin{cases} 1, \ \text{if } y_i = [V] \text{ and } x_i="knock"; \\ 0, \ \text{otherwise,} \end{cases}\]则表示观测值$x_i$为单词”knock”时,它所对应的标记很可能为$[V]$。
对比式(2)和“【机器学习基础】第六十三课:[概率图模型]马尔可夫随机场”中式(1)可看出,条件随机场和马尔可夫随机场均使用团上的势函数定义概率,两者在形式上没有显著区别;但条件随机场处理的是条件概率,而马尔可夫随机场处理的是联合概率。
2.关于式(1)的解释
根据局部马尔可夫性,给定某变量的邻接变量,则该变量独立于其他变量,即该变量只与其邻接变量有关,所以式(1)中给定变量$v$以外的所有变量与仅给定变量$v$的邻接变量是等价的。