本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
IoU也称为Jaccard index。在本篇论文的背景中,大家常用的用于计算bbox回归损失的方式有两种:
- 计算预测bbox和GT bbox对应角点之间的距离作为回归损失。这种情况下,通常用左上角和右下角的点坐标来表示bbox,即$(x_1,y_1,x_2,y_2)$。损失计算使用$\ell_2-norm$,即$\parallel \cdot \parallel_2$。
- 计算预测bbox和GT bbox对应边界之间的距离作为回归损失。这种情况下,通常用中心点和宽高来表示bbox,即$(x_c,y_c,w,h)$。损失计算使用$\ell_1-norm$,即$\parallel \cdot \parallel_1$。
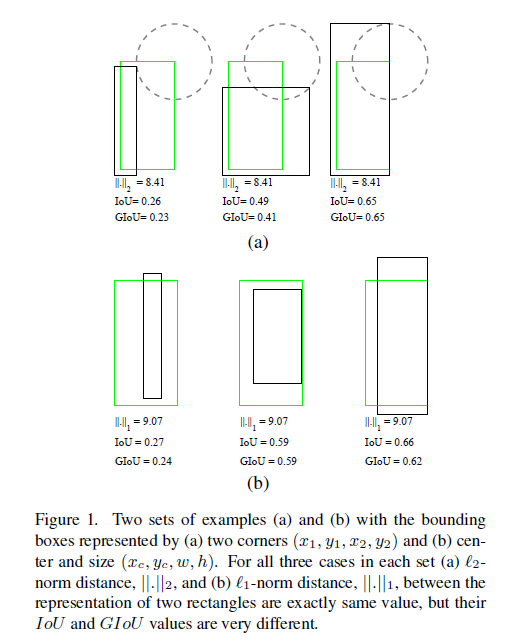
在Fig1(a)中,我们使用方法一作为回归损失,可以看到,三种情况的回归损失是一样的,但是得到的IoU或者GIoU是不一样的。同样在Fig1(b)中,我们使用方法二作为回归损失,三种情况的回归损失依旧是一样的,但是却得到了不同的IoU或GIoU。
很明显,IoU更能代表预测bbox的质量,因此我们可以直接将其作为优化的目标函数使用。但是直接使用IoU作为损失函数有以下两个缺点:
- 如果预测bbox和GT box不重叠,则IoU为0,此时无法反映两个box之间距离到底有多远。并且在这种情况下,梯度将为零,模型将无法被优化。
- 预测bbox和GT box之间不同的重叠方式可能会得到一样的IoU,此时算法无法区分这几种不同重叠方式的优劣,如Fig2所示。
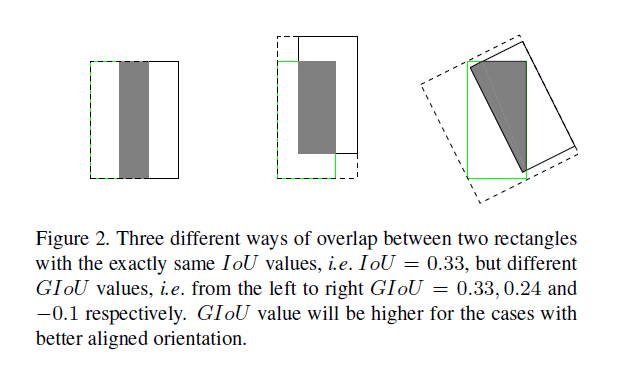
因此,我们提出了一种广义形式的IoU,称为GIoU(Generalized Intersection over Union),用来解决上面提到的两个问题。
2.Related Work
不再赘述。
3.Generalized Intersection over Union
对于任意两个形状$A,B \subseteq \mathbb{S} \in \mathbb{R}^n$,IoU的计算如下:
\[IoU = \frac{\lvert A \cap B \rvert}{\lvert A \cup B \rvert} \tag{1}\]IoU有两个优点:
- IoU损失函数很好定义,$\mathcal{L}_{IoU}=1-IoU$。
- 对box的尺度不敏感。
GIoU的计算过程如下:

对于任意两个形状$A,B \subseteq \mathbb{S} \in \mathbb{R}^n$,第一步先找到能够包裹$A,B$的最小形状$C$,如Fig2中的虚线框所示。第二步,正常计算$A,B$的IoU,即$IoU = \frac{\lvert A \cap B \rvert}{\lvert A \cup B \rvert}$。第三步,计算GIoU,即$GIoU=IoU-\frac{\lvert C \setminus (A \cup B) \rvert}{\lvert C \rvert}$。
GIoU有如下性质:
- 类似于IoU,GIoU损失函数可定义为$\mathcal{L}_{GIoU}=1-GIoU$。
- 类似于IoU,GIoU也具有尺度不变性。
- GIoU始终是IoU的下界,即有$\forall A,B \subseteq \mathbb{S} \ GIoU(A,B) \leqslant IoU(A,B)$。
- IoU的取值范围是0到1,即$\forall A,B \subseteq \mathbb{S}, \ 0 \leqslant IoU(A,B) \leqslant 1$。而GIoU的取值范围为-1到1,即$\forall A,B \subseteq \mathbb{S}, \ -1 \leqslant GIoU(A,B) \leqslant 1$。
- 与IoU不同,GIoU不仅关注重叠区域,还关注$A,B$之间的空隙区域。因此,GIoU能更好地反映两个box之间的重叠方式。
3.1.GIoU as Loss for Bounding Box Regression
$\mathcal{L}_{IoU},\mathcal{L}_{GIoU}$的计算如下所示(仅适用于box不旋转的情况):

此外,从Fig3可以看出,GIoU和IoU之间具有很强的相关性,尤其是在IoU值较高时。并且在低重叠情况下($IoU \leqslant 0.2, GIoU \leqslant 0.2$),GIoU比IoU具有更大的变化空间。因此,GIoU在这些情况下可能拥有更陡峭的梯度,这能带来更好的优化效果。
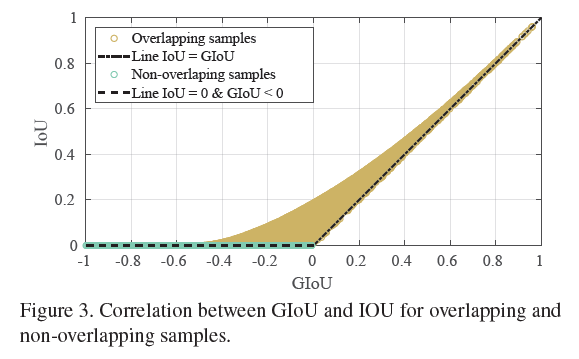
$\mathcal{L}_{IoU}$的取值范围为$[0,1]$,$\mathcal{L}_{GIoU}$的取值范围为$[0,2]$。
4.Experimental Results
4.1.YOLO v3
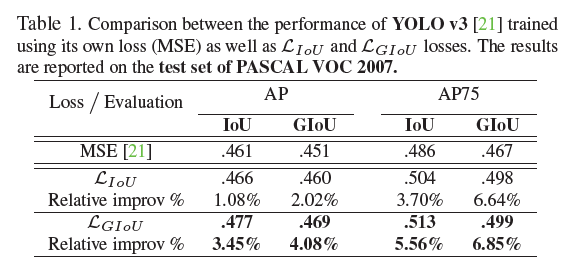
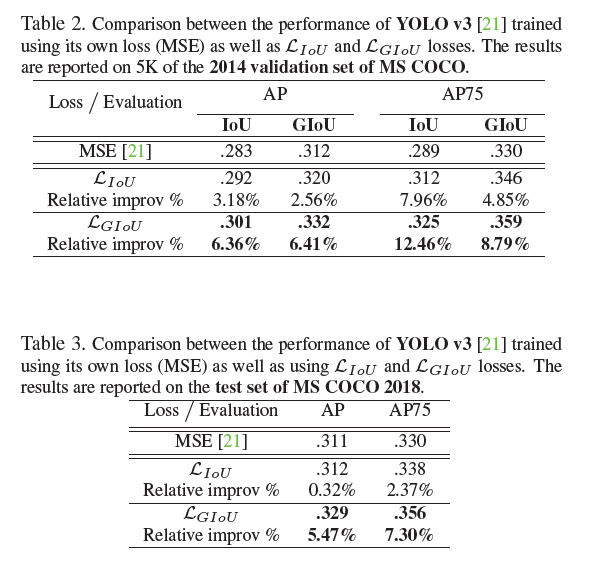
在表1中,左侧第一列$MSE,\mathcal{L}_{IoU},\mathcal{L}_{GIoU}$表示训练时所用的回归损失,AP和AP75下面的两列$IoU,GIoU$表示测试时用的评估指标。从表1可以看出,无论是使用IoU还是使用GIoU作为测试评估指标,$\mathcal{L}_{GIoU}$的性能都优于另外两种loss。
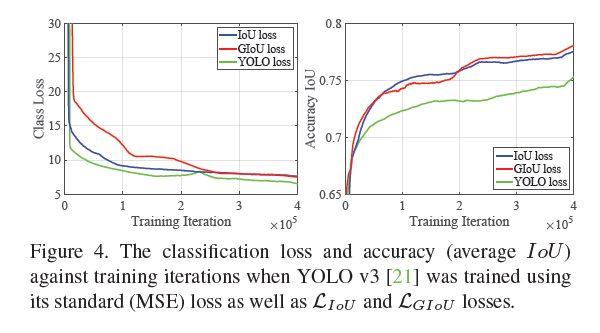

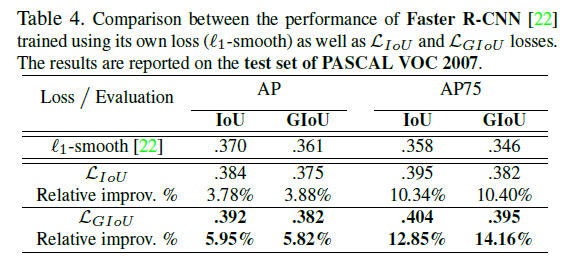
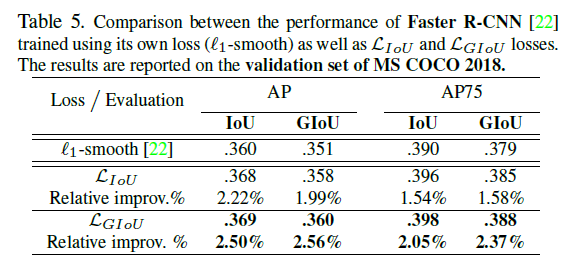
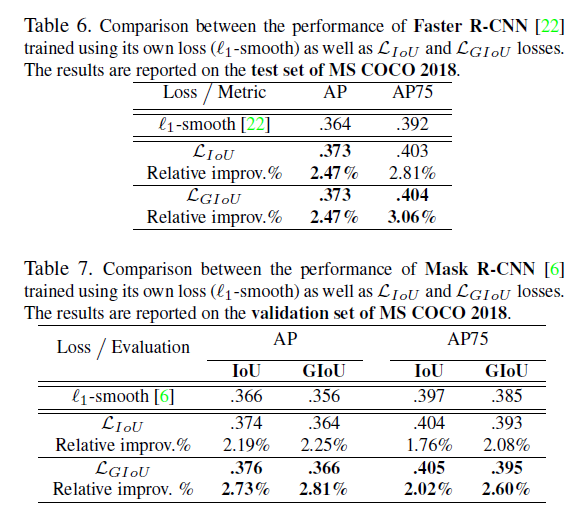
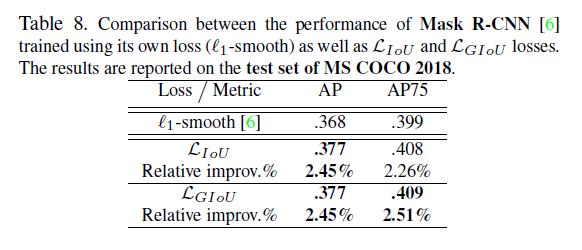
4.2.Faster R-CNN and Mask R-CNN
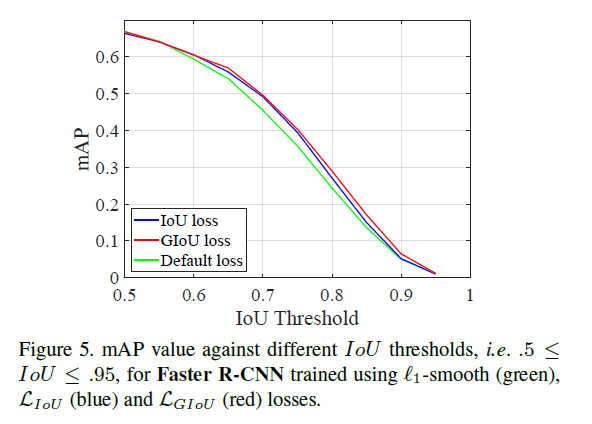

5.Conclusion
不再详述。
6.原文链接
👽Generalized Intersection over Union:A Metric and A Loss for Bounding Box Regression