【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.卷积运算
卷积运算是卷积神经网络最基本的组成部分。
1.1.边缘检测
我们通过边缘检测来说明卷积是怎么运算的。
我们在之前的博客中提到过网络的前几层一般用于检测低级特征(例如边缘等),中间几层可能会检测到物体的部分,而更靠后的层可能检测到完整的物体,如下图所示:

那么如何在图像中检测边缘呢?
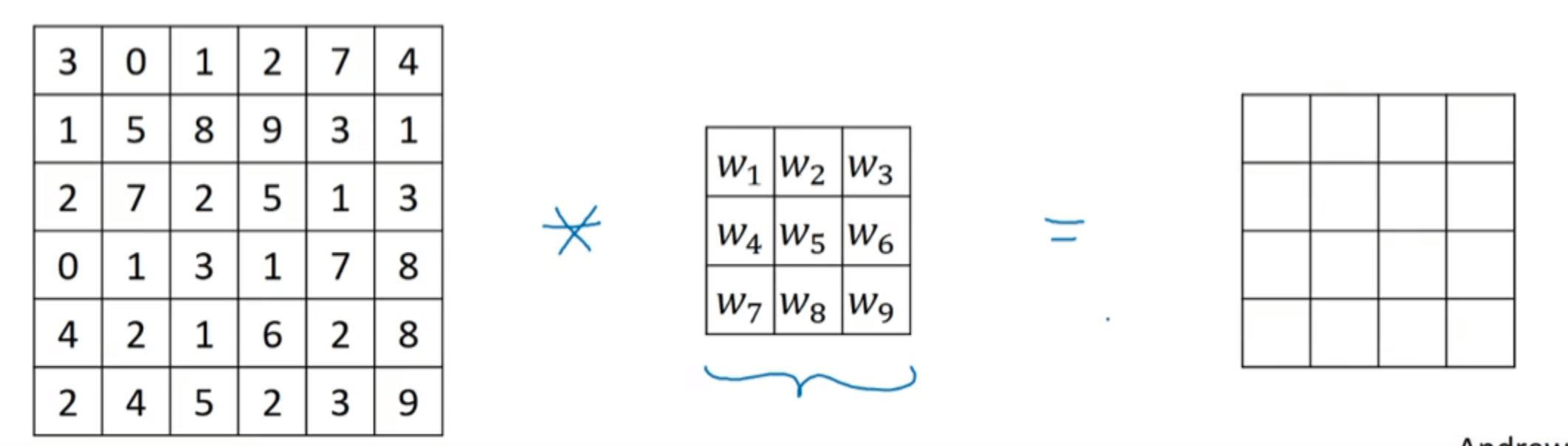
假设有一张$6 \times 6$的单通道图像,为了检测图像中的垂直边缘,我们构造一个$3\times 3$的矩阵(在卷积神经网络中通常被称为filter或者kernel),然后进行卷积运算(符号为*)得到一个$4\times 4$的矩阵:
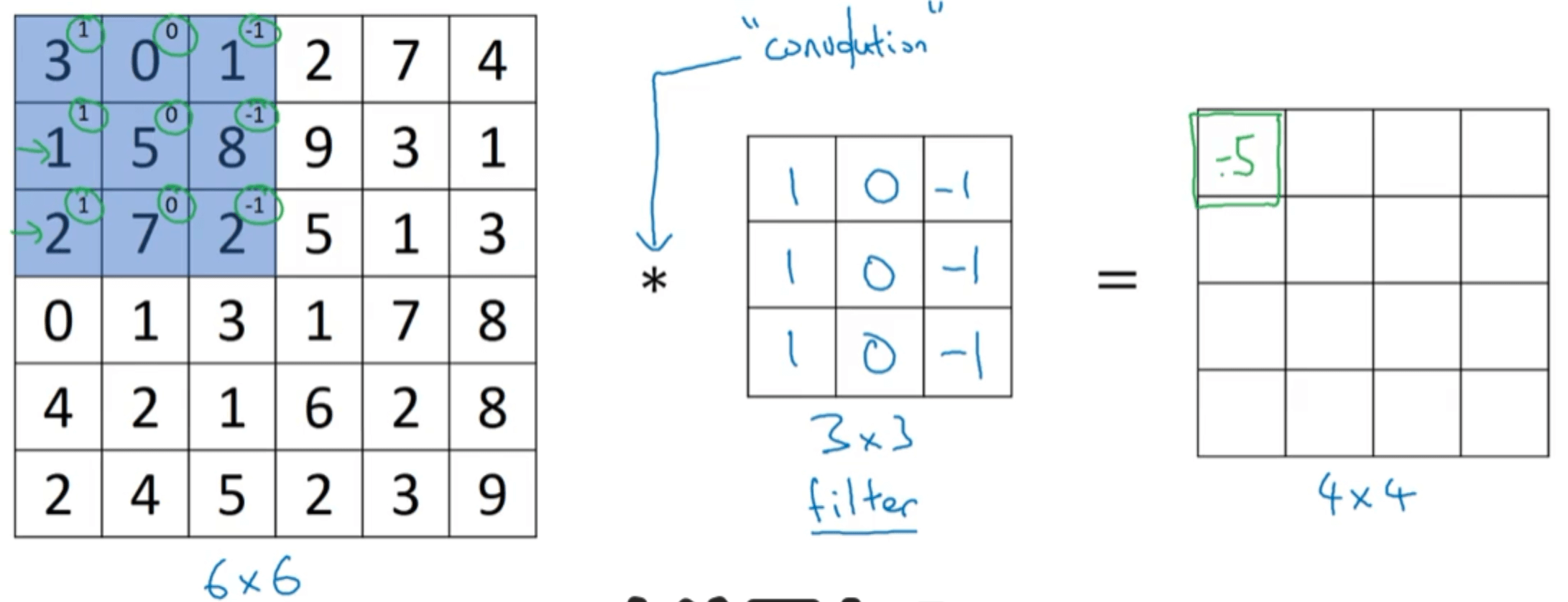
以得到$4\times 4$矩阵中第一行第一列元素的运算为例:
\[3\times 1 + 1 \times 1 + 2 \times 1 + 0\times 0 + 5 \times 0 + 7 \times 0 + 1 \times (-1) + 8 \times (-1) + 2 \times (-1)=-5\]将filter在$6\times 6$的原图中按照从左到右,从上到下的顺序依次进行上述运算,便可得到最终$4\times 4$的结果:
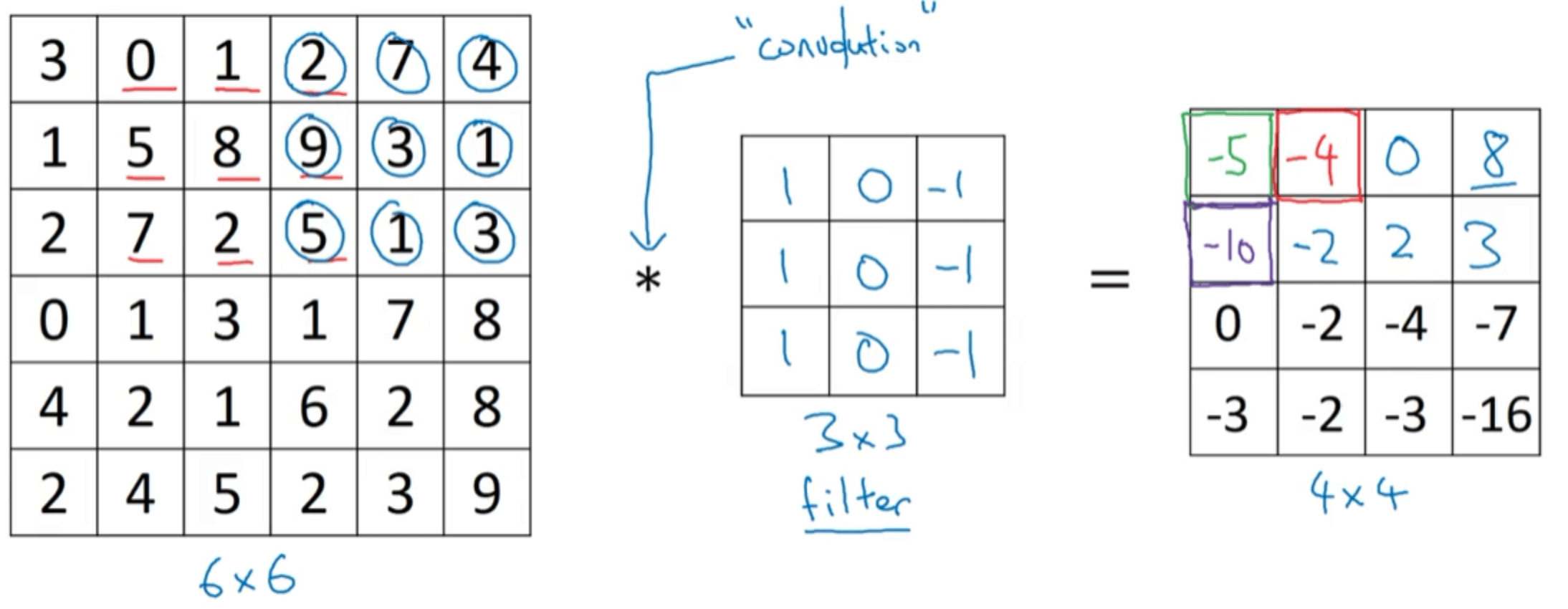
一篇讲解卷积神经网络的博客,有很多生动易懂的动图:Convolutional Neural Networks - Basics。
1.1.1.垂直边缘检测
本部分用于说明为什么上述例子中的filter可以实现垂直边缘检测:
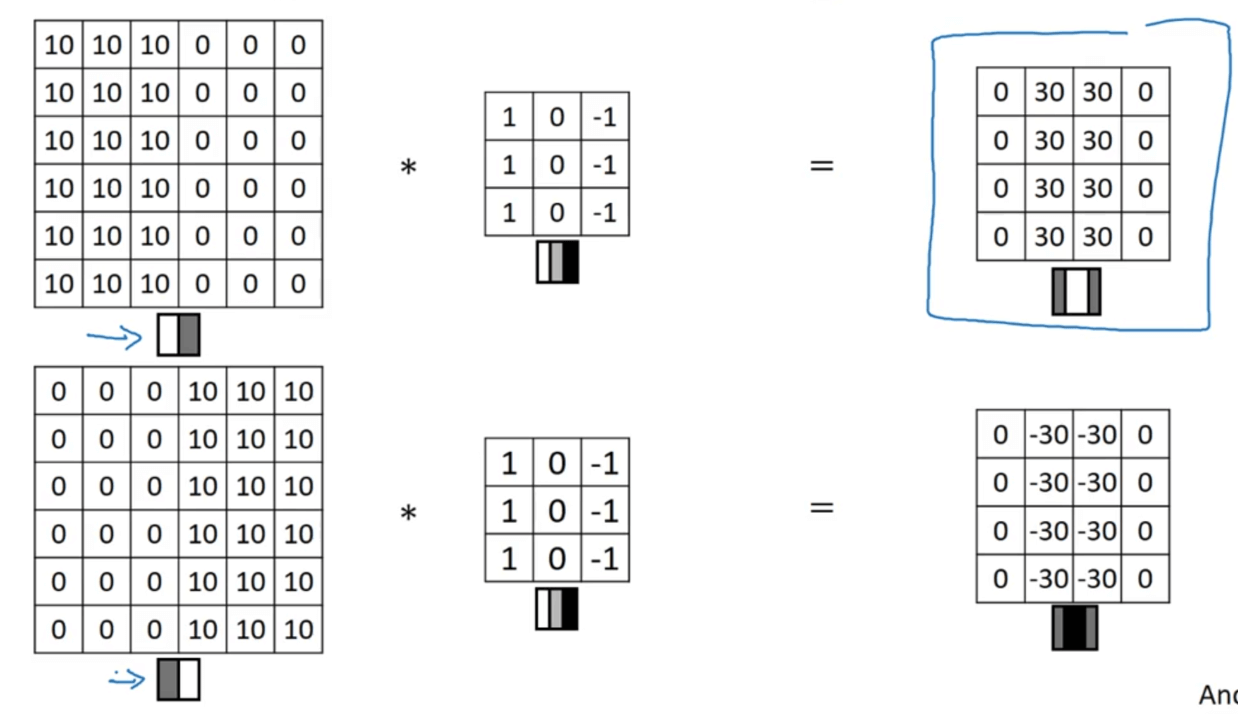
从上图中可以看出,该filter不仅可以进行垂直边缘检测,还可以判断该垂直边缘是从暗的区域过渡到亮的区域,还是从亮的区域过渡到暗的区域。如果不在乎过渡的方向,可以对得到的矩阵取绝对值。
垂直边缘检测filter内的值不一定非得是1和-1,也可以是其他合理的值,常用的例如:
👉sobel filter:
\[\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \\ \end{bmatrix}\]👉scharr filter:
\[\begin{bmatrix} 3 & 0 & -3 \\ 10 & 0 & -10 \\ 3 & 0 & -3 \\ \end{bmatrix}\]1.1.2.水平边缘检测
类似的,我们可以构建用于提取水平边缘的filter:
\[\begin{bmatrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \\ \end{bmatrix}\]同样的,将1.1.1部分中的sobel filter和scharr filter旋转$90^0$便可得到对应的水平边缘检测filter。
1.2.实际应用
在实际应用时,filter内都被填充上参数,然后通过反向传播进行优化,举例如下:
1.3.cross-correlation和convolution
数学教材中定义的卷积运算(convolution):

会先将filter做一个翻转,然后再执行我们在1.1部分中提到的计算(该计算方式在数学中被称为cross-correlation)。
但是在深度学习中,我们将这种省去了翻转步骤的cross-correlation直接称呼为convolution,这点和数学教材中是有差异的。
2.Padding
第1部分中我们可以看到,一个$n \times n$的输入,在经过一个$f\times f$的filter卷积运算后($f$通常为奇数),输出的维度变为$(n-f+1) \times (n-f+1)$。这样存在两个问题:1)每次做卷积操作,输出会变得越来越小;2)位于输入边缘的元素相比位于中间的元素在卷积运算时少被使用很多次。
我们使用padding来解决这两个问题。padding主要分为两种方式:SAME和VALID。
2.1.SAME
SAME方式是在输入的周围填补新的边缘(通常用0填补),例如:

在上图中,我们只填补了一圈,即$p=1$。输出的维度变为$(n+2p-f+1) \times (n+2p-f+1)$。
如果想让输入和输出的维度保持一致,则令$p=\frac{f-1}{2}$即可。
2.2.VALID
VALID方式意味着不填充,即不做padding。
3.步长(Stride)
卷积中的步长是另一个构建卷积神经网络的基本操作。
之前的例子中我们都默认步长为1,即filter每次只移动一个单位,如果filter每次移动两个单位,即步长为2:

如果输入的维度为$n\times n$,filter大小为$f\times f$,padding填充的圈数为p,步长为s,则最终得到的输出维度为:
\[\lfloor \frac{n+2p-f}{s} +1 \rfloor \times \lfloor \frac{n+2p-f}{s} +1 \rfloor\]$\lfloor \rfloor$表示向下取整。即上式需保证整个filter都在输入的维度范围之内。
4.三维卷积
之前我们讨论的输入都是二维的,现在我们来看下输入维度为三维该怎么进行卷积运算。
假设输入为RGB图像,维度为$6\times 6 \times 3$(即height $\times$ width $\times$ channel)。相应的,构建的filter的维度也应该是三维的,例如$3\times 3 \times 3$(即height $\times$ width $\times$ channel,filter的通道数目必须和输入的通道数目一致)。⚠️这里需要特别注意的一点是:我们得到的输出维度为$4 \times 4$(假设无padding,s=1,只有一个filter):

卷积运算和输入为二维时类似,将filter中的27个参数分别与输入中对应的值相乘,然后再求和,得到输出对应位置的值。
举个例子,假如我们只想检测R通道的垂直边缘,那么我们可以这样设置filter:
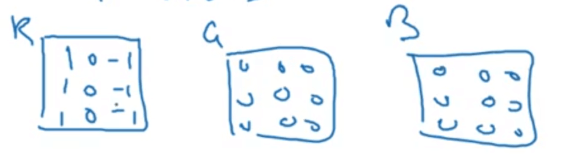
扩展一下,如果我们想检测多种特征,即我们想使用多个不同的filter,假设我们用了2个filter,那么我们得到的输出维度就变为$4 \times 4 \times 2$:
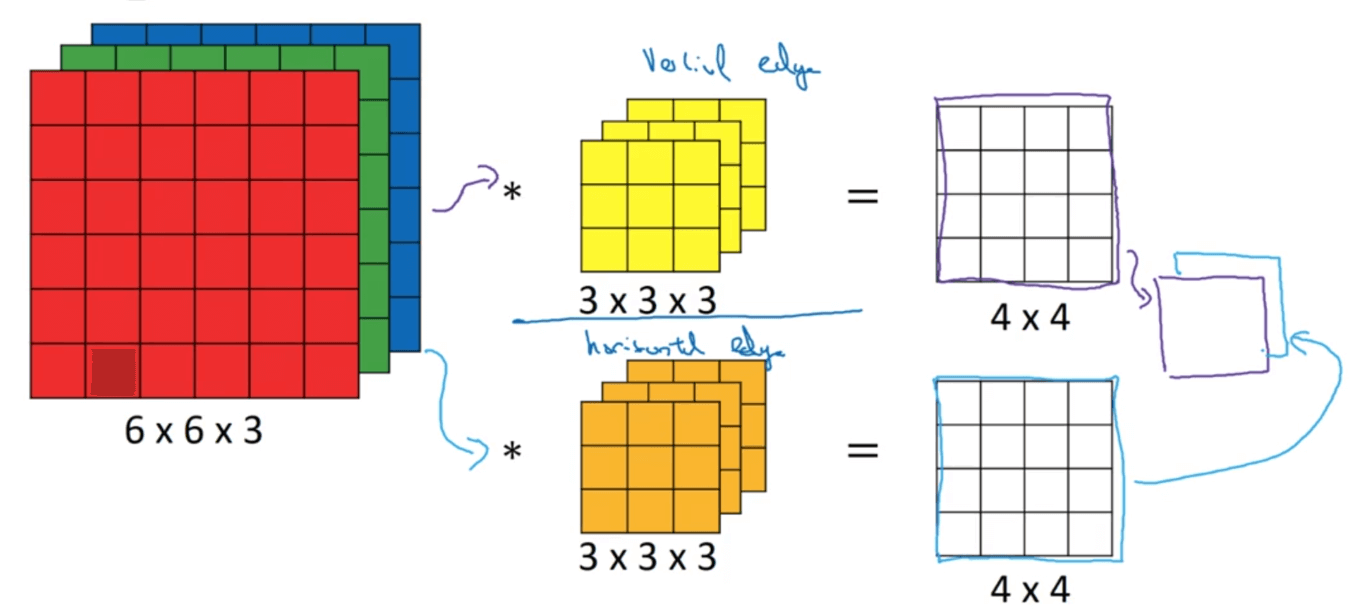
总结一下,假设输入的维度为$n \times n \times n_c$,共使用了$n_c’$个filter,每个filter的大小为$f \times f \times n_c$,则我们得到的输出的维度为:
\[\lfloor \frac{n+2p-f}{s} +1 \rfloor \times \lfloor \frac{n+2p-f}{s} +1 \rfloor \times n_c'\]通道数目$n_c$有时也被称为深度。
如果输入的height和width不相等,即$n_H \times n_W \times n_c$,则我们得到的输出的维度为:
\[\lfloor \frac{n_H+2p-f}{s} +1 \rfloor \times \lfloor \frac{n_W+2p-f}{s} +1 \rfloor \times n_c'\]5.卷积层
‼️一个典型的卷积网络通常有三层:
- 卷积层(Convolution,简写为CONV)。
- 池化层(Pooling,简写为POOL)。
- 全连接层(Fully connected,简写为FC)。
全连接层我们已经在之前的博客中见到过,即上一层的每一个神经元都与下一层的每一个神经元相连接,例如:
虽然仅用卷积层也有可能构建出很好的神经网络,但大部分神经网络架构依然会添加池化层和全连接层。本节我们先了解卷积层的构建,后面两节会讲解池化层和全连接层的构建。
5.1.一个卷积层

上图展示了如何构建一个简单的卷积层(使用了2个filter,激活函数为RELU函数)。
5.2.多个卷积层

6.池化层
卷积神经网络经常用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性。
Pooling分为两种方式:
- Max pooling
- Average pooling
6.1.Max pooling
假设$f=2,s=2$,取每个区域对应的最大值:
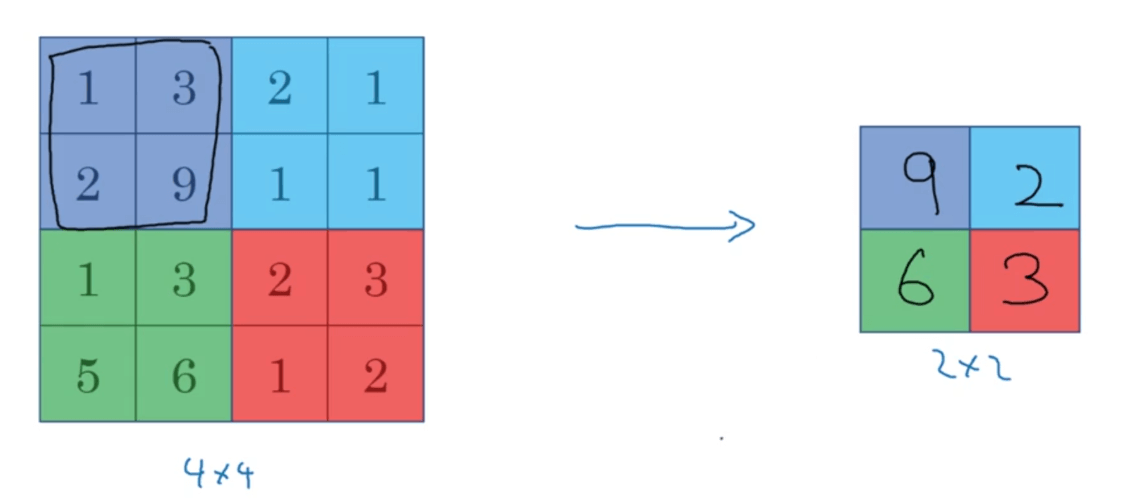
举另外一个例子,$f=3,s=1$:
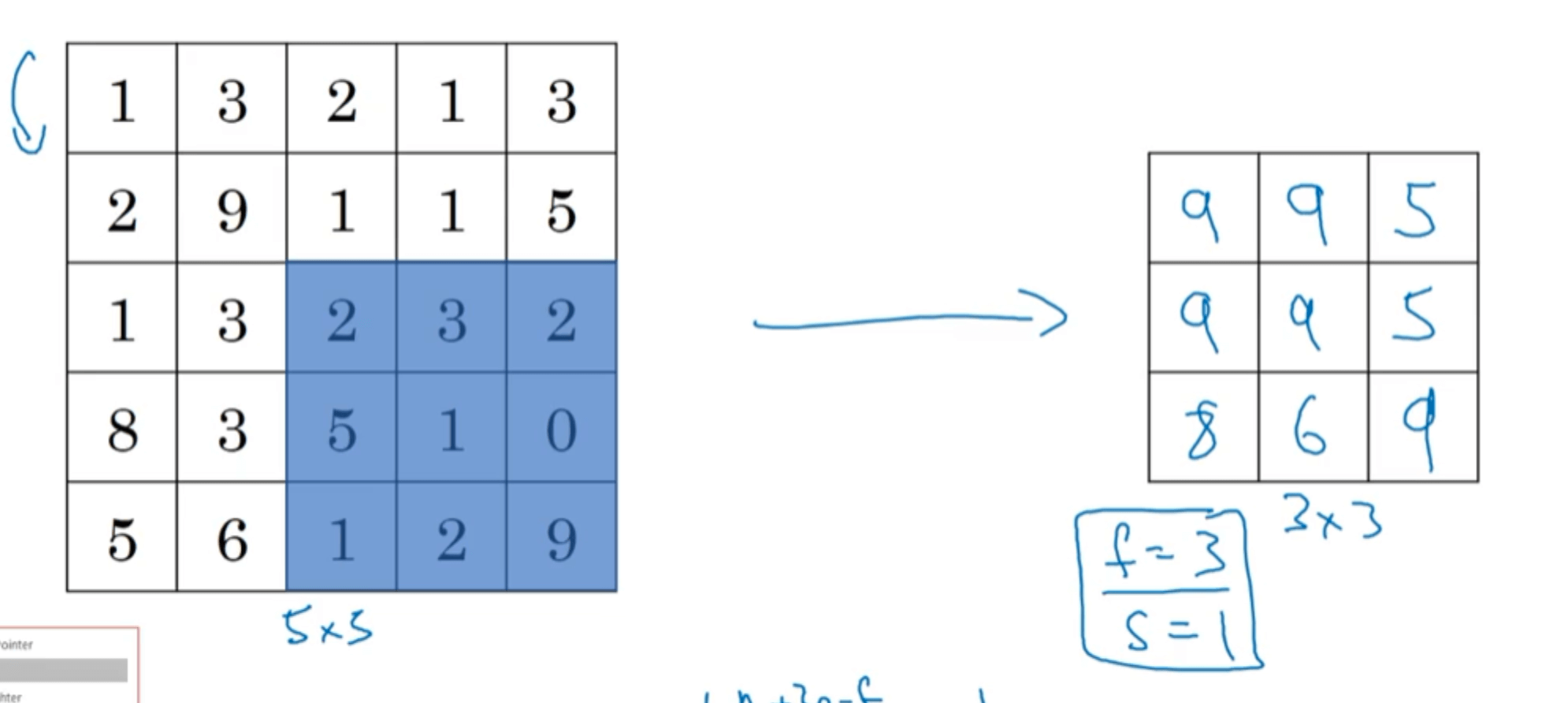
如果输入是三维的,那么对应的池化层的输出也是三维的,即对每一个通道分别做最大池化。例如输入维度为:$5\times 5 \times 2$,则池化层输出维度为$3\times 3 \times 2$。
👉Max pooling的反向传播:
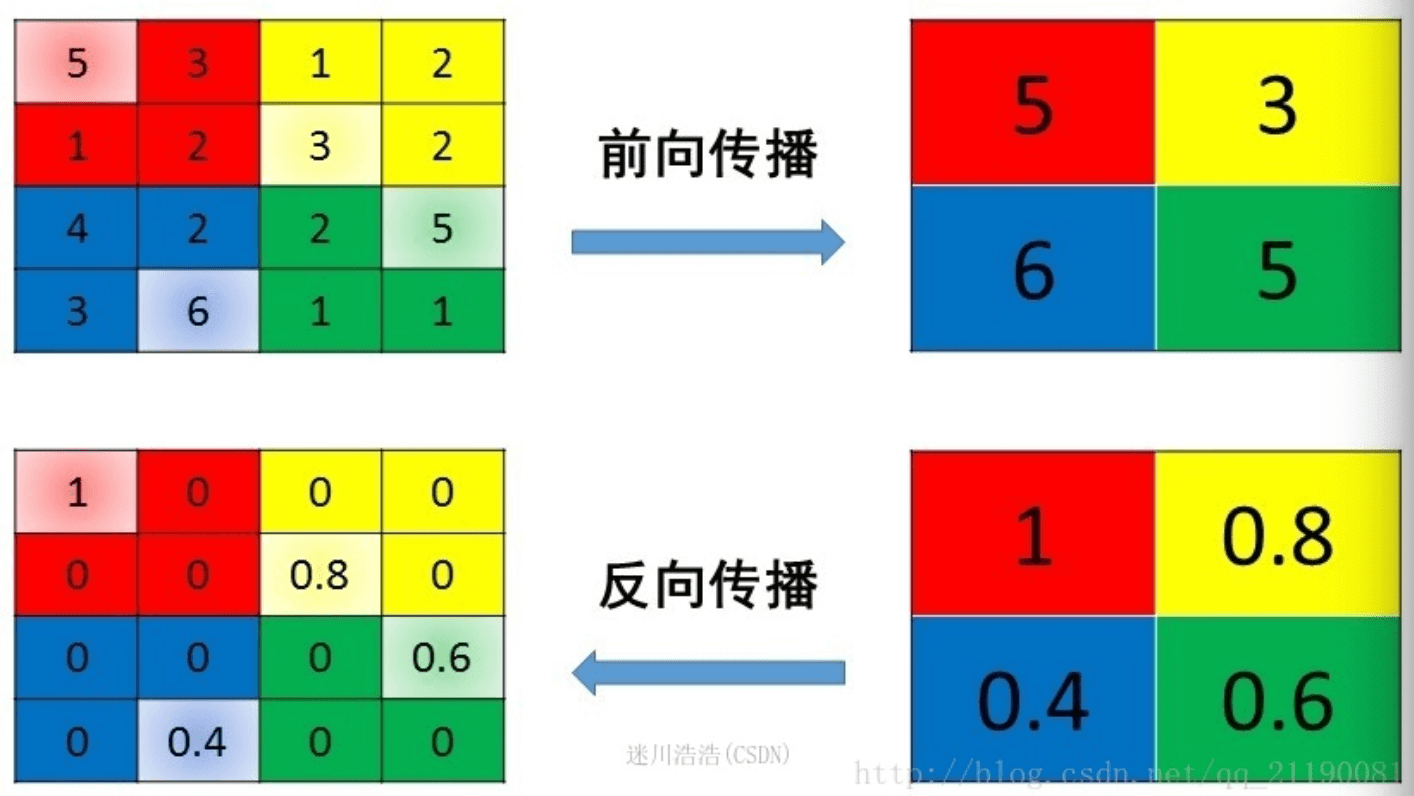
6.2.Average pooling
假设$f=2,s=2$,取每个区域对应的平均值:

相比Max pooling,Average pooling用的相对较少。
👉Average pooling的反向传播:
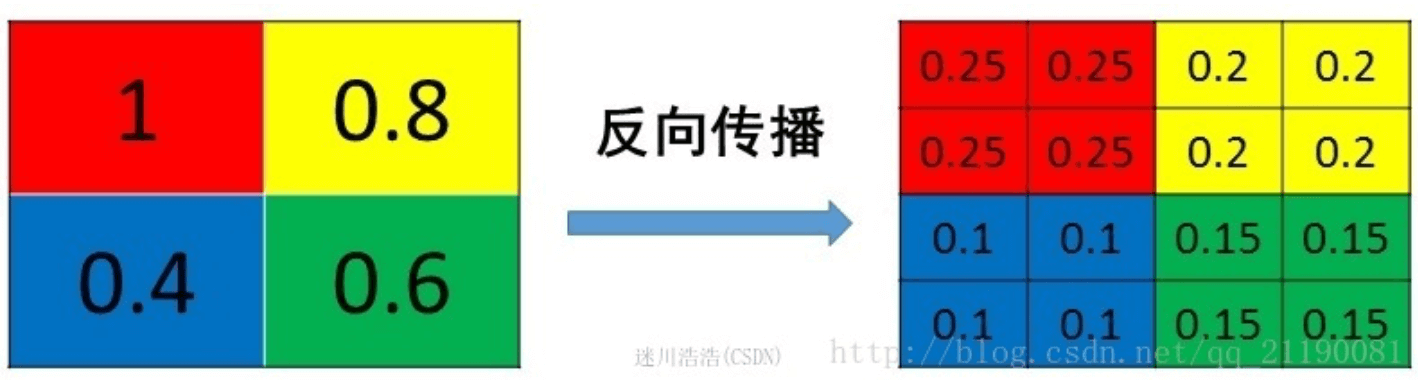
7.卷积神经网络示例
比如我们搭建一个用于识别手写数字的卷积神经网络:
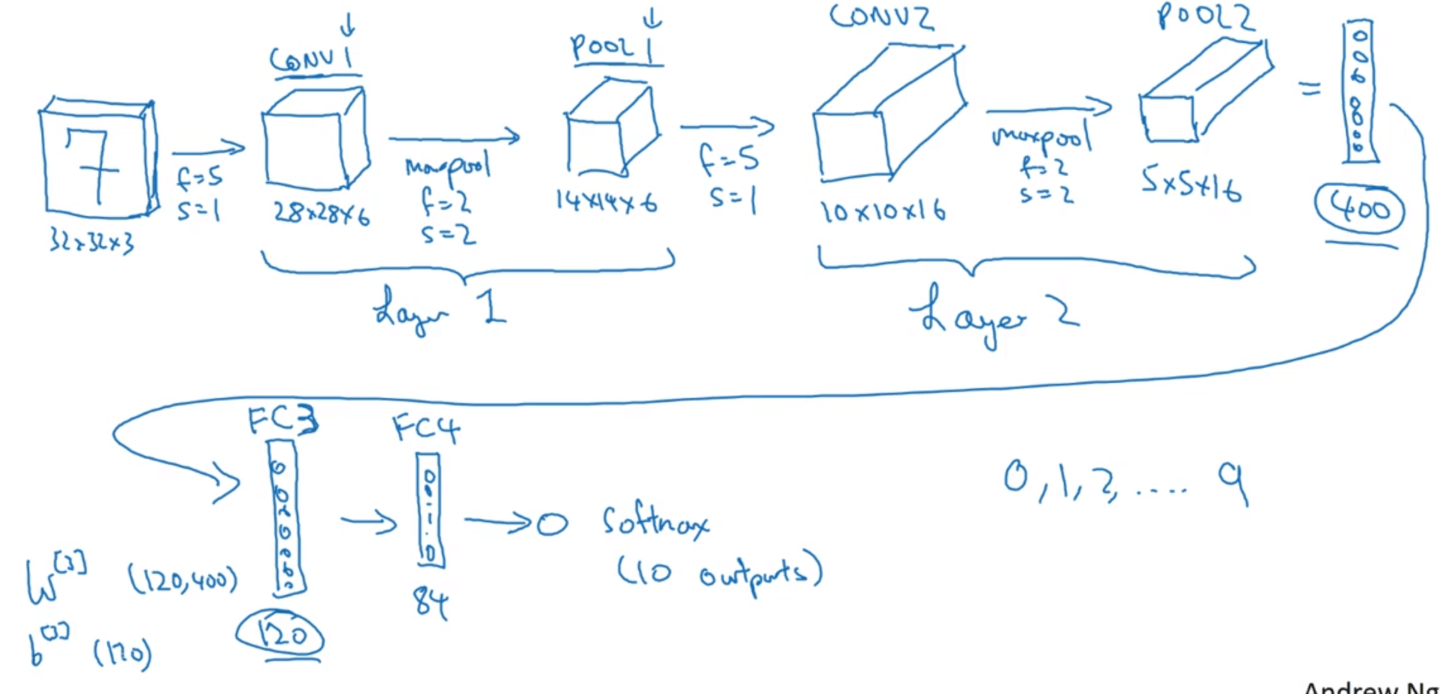
关于层数的划分通常有两种不同的看法:1)一个卷积层及一个池化层被看作为神经网络中的一层;2)一个卷积层为一层,一个池化层为另一层。但是在计算神经网络的层数时,通常只是统计具有权重(参数)的层,因为池化层没有权重(参数),所以我们更倾向于第一种划分方法。
随着神经网络深度的加深,高度$n_H$和宽度$n_W$通常都会随之减小,而通道$n_c$的数量会随之增加。
在神经网络中,另一种常见模式就是在一个或多个卷积层后面跟随一个池化层,然后再是一个或多个卷积层后面跟随一个池化层,最后是几个全连接层。
上述示例中每一层输出的维度以及参数数量统计:
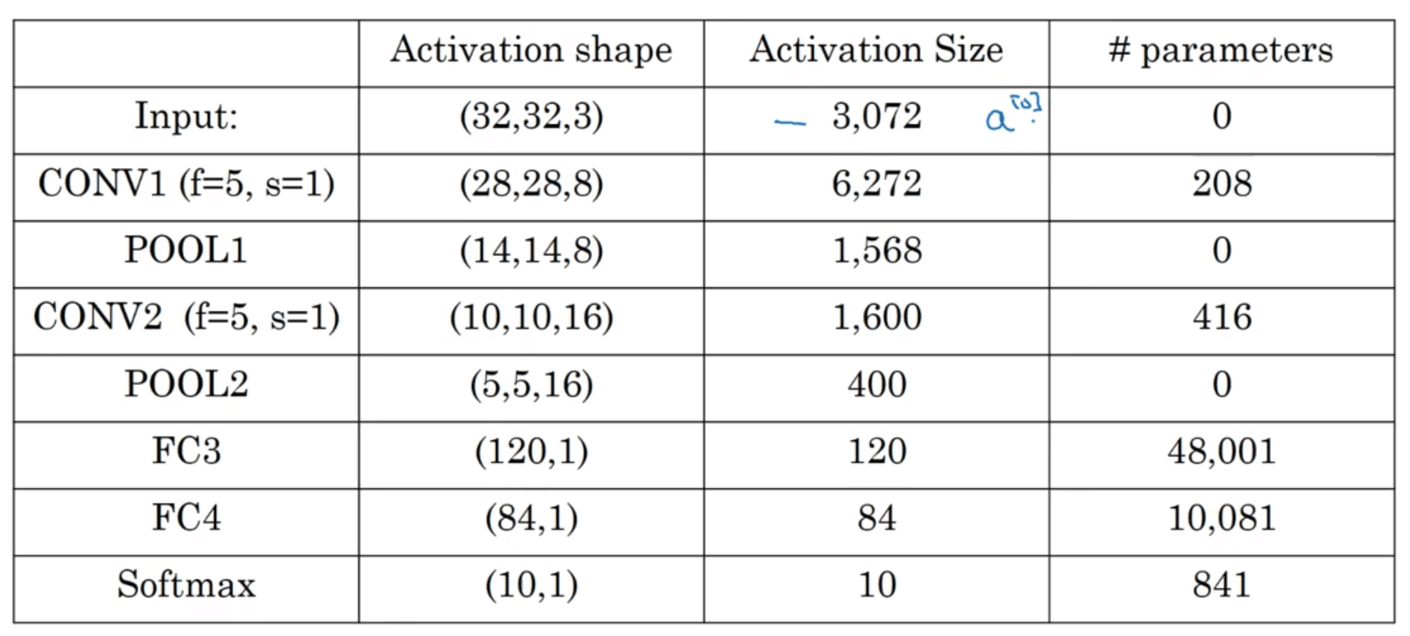
计算参数数量时记得加上偏置项b。
需要注意几点:
- 池化层没有参数。
- 卷积层的参数相对较少,全连接层的参数较多。
- 通常情况下,随着神经网络的加深,Activation Size逐渐变小。如果该值下降太快,可能会影响网络性能。
8.为什么要用卷积层
和只用全连接层相比,卷积层的两个主要优势在于:1)参数共享;2)稀疏连接。
举个例子:
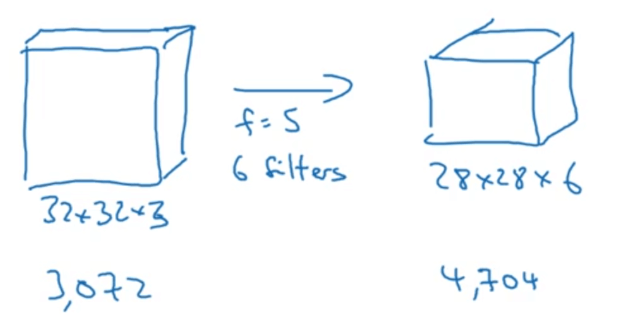
如果使用全连接层,则参数数量为:$3072\times 4704=14,450,688$。如果使用卷积层,则参数数量为:$5\times 5 \times 3 \times6 + 6=456$。