本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.相似矩阵
在线性代数中,相似矩阵(similar matrix)是指存在相似关系的矩阵。相似关系是两个矩阵之间的一种等价关系。两个$n \times n$矩阵A与B为相似矩阵当且仅当存在一个$n \times n$的可逆矩阵P,使得:
\[P^{-1}AP=B\]P被称为矩阵A与B之间的相似变换矩阵。
例如:
\[\begin{bmatrix} 2 & 1 \\ 1 & -1 \\ \end{bmatrix}^{-1} \begin{bmatrix} 1 & 2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 1 & -1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 0 \\ 0 & -1 \\ \end{bmatrix}\] \[\begin{bmatrix} 1 & 2 \\ -2 & 1 \\ \end{bmatrix}^{-1} \begin{bmatrix} 8 & -6 \\ -6 & 17 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 \\ -2 & 1 \\ \end{bmatrix} = \begin{bmatrix} 20 & 0 \\ 0 & 5 \\ \end{bmatrix}\]1.1.相似变换的几何意义
👉相似矩阵的几何意义就是同一个线性变换在不同的基下的表达形式(关于线性变换请见:线性变换,即$Q=P$且均为方阵的情况)。
举个例子,线性变换$T:V\to V$,在$y=x$方向拉伸两倍:
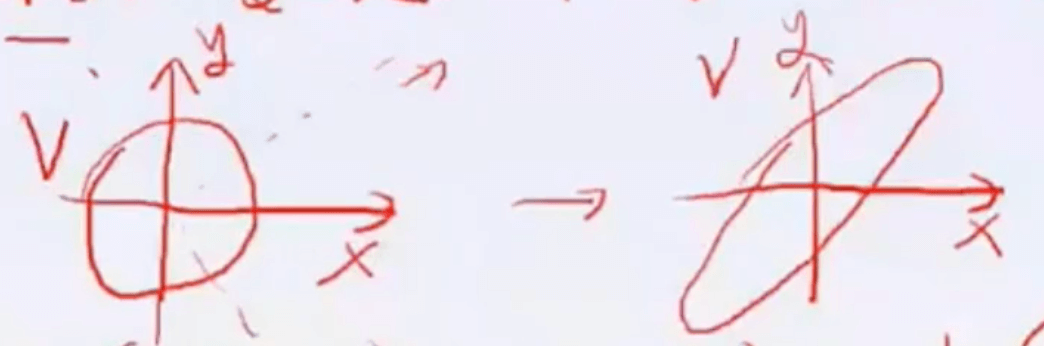
选择第一组基为:$\alpha=\{ \alpha_1=(1,0),\alpha_2=(0,1) \}$,则有:
\[T(\alpha_1+\alpha_2)=2(\alpha_1 + \alpha_2)\] \[T(\alpha_1 - \alpha_2)=\alpha_1 - \alpha_2\]根据上面两个式子可得:
\[T(\alpha_1)=\frac{3}{2}\alpha_1 + \frac{1}{2} \alpha_2\] \[T(\alpha_2)=\frac{1}{2} \alpha_1 + \frac{3}{2} \alpha_2\]因此:
\[A_{\alpha}(T)=\begin{bmatrix} \frac{3}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{3}{2} \\ \end{bmatrix}\]此时,我们再换另外一组基:$\tilde{\alpha}=\{ \alpha_1=(1,1), \alpha_2=(1,-1) \}$
类似的,我们可以求得:
\[T(\tilde{\alpha_1})=2 \tilde{\alpha_1}\] \[T(\tilde{\alpha_2})=\tilde {\alpha_2}\] \[A_{\tilde{\alpha}}(T)=\begin{bmatrix} 2 & 0 \\ 0 & 1 \\ \end{bmatrix}\]1.2.相似变换下的不变性质
两个相似的矩阵有许多相同的性质(这里仅列出部分性质):
1.2.1.矩阵的特征值和特征向量
设$A$是$n$阶方阵,如果数$\lambda$和$n$维非零列向量$x$使关系式$Ax=\lambda x$成立,那么这样的数$\lambda$称为矩阵$A$的特征值,非零向量$x$称为$A$对应于特征值$\lambda$的特征向量。
特征方程:$det(A-\lambda I)=0$,$I$为单位矩阵。
❗️$A$的迹等于所有特征值之和。
👉举个例子:
\[A=\begin{bmatrix} 2 & 1 \\ 1 & 2 \\ \end{bmatrix}\]$A-\lambda I$为:
\[A=\begin{bmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \\ \end{bmatrix}\] \[det(A-\lambda I)=(2-\lambda)^2 -1=(\lambda -1)(\lambda -3)=0\]解得两个特征值:$\lambda_1=1;\lambda_2=3$。
$Ax=\lambda x$等价于$(A-\lambda I)x=0$,分别代入$\lambda_1,\lambda_2$求得对应的特征向量:
\[\begin{bmatrix} 2-1 & 1 \\ 1 & 2-1 \\ \end{bmatrix} x = \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ \end{bmatrix}x=0 \Rightarrow x_1=\begin{bmatrix} 1 \\ -1 \\ \end{bmatrix}\] \[\begin{bmatrix} 2-3 & 1 \\ 1 & 2-3 \\ \end{bmatrix} x = \begin{bmatrix} -1 & 1 \\ 1 & -1 \\ \end{bmatrix}x=0 \Rightarrow x_2=\begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}\]$x_1,x_2$乘以某一系数结果依旧成立。
‼️矩阵和其特征值存在两个非常重要的关系:假设矩阵$A$的特征值为$a_1,a_2,a_3,…,a_n$(重根重复记),则:
\[\sum a_i = \text{trace} (A)\] \[\prod a_i = \text{det} (A)\]2.相合变换
如果对于两个对称方阵$A$和$\tilde A$,存在一个可逆方阵$P$,使得$\tilde A=P^T AP$。那么这两个方阵就互为相合矩阵。
2.1.相合不变量
- 矩阵的正定性(正定,负定)。
- 矩阵的正负特征值的个数。
- 相合变换下矩阵保持对称性。
3.正交相似变换
如果两个对称方阵$A$和$\tilde A$满足,$\tilde A=P^T AP$,而且$P$是正交矩阵:$P^T=P^{-1}$,那么这$A$与$\tilde A$就互为正交相似。
正交矩阵:方阵$Q$满足,$Q^T Q=Q Q^T=I$(等价于$Q^T=Q^{-1}$),其中$I$为单位矩阵。
若内积空间中两向量的内积为0,则称它们是正交的。
正交相似变换同时满足相似和相合变换的条件,也就是说它同时保持了矩阵的相似与相合不变量。
‼️任何一个对称矩阵$A$都可以正交相似于一个对角矩阵$D$。即总存在一个正交矩阵$P$使得,$A=P^T DP$。
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵。对角线上的元素可以为0或其他值。