【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.理解超平面
1.1.二维平面
超平面是支持向量机中非常重要的一个概念,再介绍超平面之前,我们来介绍下常见的二维平面的一些性质。
👉在三维x-y-z坐标系中,可以将平面定义为一个方程的集:
\[ax+by+cz+d=0\]其中$a,b,c,d$是实数,使得$a,b,c$不全为0。平面的法向量为$(a,b,c)$。
👉由一点和一个法向量决定的平面:
对于一点$P_0=(x_0,y_0,z_0)$和一个向量$\vec n=(a,b,c)$,平面方程为:
\[ax+by+cz=ax_0+by_0+cz_0\]这是穿过点$P_0$并垂直于向量$\vec n$的平面。
👉通过三点的平面:
穿过三点$P_1=(x_1,y_1,z_1),P_2=(x_2,y_2,z_2),P_3=(x_3,y_3,z_3)$的平面的方程可以表述为如下行列式:
\[\begin{vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \\ \end{vmatrix}=0\]👉一点到平面的距离:
对于一点$P_1=(x_1,y_1,z_1)$和一个平面$ax+by+cz+d=0$,从点$P_1$到平面的距离是:
\[D=\frac{\mid ax_1+by_1+cz_1+d \mid}{\sqrt {a^2+b^2+c^2}}\]👉判定两个平面平行:
设两平面$\alpha,\beta$的方程分别为:
\[\alpha:A_1 x+B_1y+C_1z+D_1=0\] \[\beta:A_2 x+B_2y+C_2z+D_2=0\]其法向量分别为$\vec {n_1}=\{ A_1,B_1,C_1 \}$和$\vec {n_2}=\{ A_2,B_2,C_2 \}$。两平面平行的充要条件:
\[\vec{n_1} // \vec{n_2}\]即:
\[\vec{n_1} = \lambda \vec{n_2}\]用分量来表示为:
\[A_1=\lambda A_2,B_1=\lambda B_2,C_1=\lambda C_2\]亦即:
\[\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}=\lambda\]👉两平行平面之间的距离:
假设两平行平面分别为(系数化为一样):
\[\alpha : ax+by+cz+d_1=0\] \[\beta : ax+by+cz+d_2=0\]则两平面之间的距离为:
\[\frac{\mid d_1 - d_2 \mid}{\sqrt{a^2+b^2+c^2}}\]1.2.超平面
在数学中,超平面(hyperplane)是n维欧氏空间中,余维度为1的子空间。即超平面是n维空间中的n-1维的子空间。它是平面中的直线、空间中的平面之推广。
设F为域(为初等起见,可考虑$F=\mathbb R$)。n维空间$F^n$中的超平面是由方程:
\[a_1x_1 + ...... + a_n x_n=b\]定义的子集,其中$a_1,…,a_n \in F$是不全为零的常数。
1.1部分中二维平面的性质也可推广到超平面。
2.间隔与支持向量
给定训练样本集$D=\{ (\mathbf x_1,y_1),(\mathbf x_2,y_2),…,(\mathbf x_m,y_m) \},y_i \in \{ -1,+1 \}$,分类学习最基本的想法就是基于训练集$D$在样本空间中找到一个划分超平面,将不同类别的样本分开。但能将训练样本分开的划分超平面可能有很多,如下图所示,我们应该努力去找到哪一个呢?
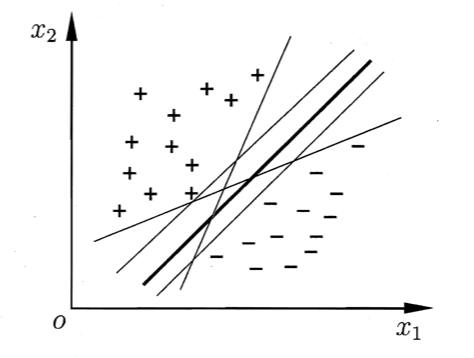
直观上看,应该去找位于两类训练样本“正中间”的划分超平面,即上图中加粗的那个,因为该划分超平面对训练样本局部扰动的“容忍”性最好。例如,由于训练集的局限性或噪声的因素,训练集外的样本可能比上图中的训练样本更接近两个类的分隔界,这将使许多划分超平面出现错误,而加粗的超平面受影响最小。换言之,这个划分超平面所产生的分类结果是最鲁棒的,对未见示例的泛化能力最强。
在样本空间中,划分超平面可通过如下线性方程来描述:
\[\mathbf w^T \mathbf x +b = 0\]其中$\mathbf w=(w_1;w_2;…;w_d)$为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离。显然,划分超平面可被法向量$\mathbf w$和位移b确定,我们将其记为$(\mathbf w,b)$。样本空间中任意点$\mathbf x$到超平面$(\mathbf w,b)$的距离可写为:
\[r=\frac{\mid \mathbf w^T \mathbf x +b \mid}{\lVert \mathbf w \rVert}\]假设如下红色所示超平面$(\mathbf w,b)$能将训练样本正确分类,即对于$(\mathbf x_i,y_i) \in D$,若$y_i=+1$,则有$\mathbf w^T \mathbf x_i +b>0$;若$y_i=-1$,则有$\mathbf w^T \mathbf x_i +b<0$。

此外还有两个虚线所示的超平面与红色超平面平行,且可以做到刚好分类成功。因此分类器可以进一步描述为:
\[\left\{ \begin{array}{c} \mathbf w^T \mathbf x_i +b \geqslant +k, y_i=+1 \\ \mathbf w^T \mathbf x_i +b \leqslant -k, y_i=-1 \\ \end{array} \right. \tag{1}\]如上图所示,距离红色超平面最近的这几个训练样本点使式(1)的等号成立,它们被称为“支持向量”(support vector)。
之所以将样本称之为向量,是因为每个样本都对应一个特征向量。
两个异类支持向量到红色超平面的距离之和为(即两个虚线所示超平面之间的距离):
\[\gamma = \frac{2k}{\lVert \mathbf w \rVert}\]它被称为“间隔”(margin)。
若超平面$(\mathbf w’,b’)$能将训练样本正确分类,则总存在缩放变换$\xi \mathbf w \mapsto \mathbf w’$和$\xi b \mapsto b’$使式(1)成立。因此,式(1)我们可以简化为:
\[\left\{ \begin{array}{c} \mathbf w^T \mathbf x_i +b \geqslant +1, y_i=+1 \\ \mathbf w^T \mathbf x_i +b \leqslant -1, y_i=-1 \\ \end{array} \right. \tag{2}\]对应的间隔为:
\[\gamma = \frac{2}{\lVert \mathbf w \rVert}\]欲找到具有“最大间隔”(maximum margin)的划分超平面,也就是要找到能满足式(2)中约束的参数$\mathbf w$和$b$,使得$\gamma$最大,即:
\[\begin{align*} &\max \limits_{\mathbf w,b} \quad \frac{2}{\lVert \mathbf w \rVert} \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& y_i(\mathbf w^T \mathbf x_i +b) \geqslant 1,i=1,2,...,m \\ \end{array} \end{align*}\]上式等价于:
\[\begin{align*} &\min \limits_{\mathbf w,b} \quad \frac{1}{2} \lVert \mathbf w \rVert ^2 \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& y_i(\mathbf w^T \mathbf x_i +b) \geqslant 1,i=1,2,...,m \\ \end{array} \end{align*}\]这就是支持向量机(Support Vector Machine,简称SVM)的基本型。
间隔貌似仅与$\mathbf w$有关,但事实上$b$通过约束隐式地影响着$\mathbf w$的取值,进而对间隔产生影响。