本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.介绍(INTRODUCTION)
VGG是由Oxford名为Visual Geometry Group的小组提出的,VGG的名字也是来自其组名首字母的缩写。VGG是ILSVRC2014的亚军,其在AlexNet的基础上,使用更小的卷积核,并尝试从增加深度的方面改善其性能。
2.网络配置(CONVNET CONFIGURATIONS)
VGG中所有卷积层的设置都是一样的。
2.1.网络结构(ARCHITECTURE)
网络的输入为$224\times 224$的RGB图像。唯一做的预处理是对每个像素减去训练集中的RGB均值。卷积核的大小基本都为$3\times 3$,在其中一个配置中,作者使用了$1\times 1$的卷积核。filter的步长恒定为1。padding的方式为保持输入的维度不变,即如果使用$3\times 3$的卷积核,步长为1,那么padding=1。pooling采用max-pooling的方式,核大小为$2\times 2$,步长为2,但并不是所有卷积层后面都跟有max-pooling,只有部分卷积层后面有max-pooling。
在一系列卷积层后是三个全连接层:前两个全连接层有4096个神经元,最后一个全连接层有1000个神经元,对应ILSVRC比赛的1000个类别。最后一层的激活函数为softmax。全连接层的参数配置在所有VGG网络结构中都是一样的。
所有隐藏层的激活函数都是ReLU。只有一个VGG网络结构中包含了LRN(LRN的参数设置和AlexNet原文中保持一致),剩余的VGG网络结构均未使用LRN。VGG的作者发现LRN非但不能改善模型在ILSVRC数据集上的表现,并且还会造成内存占用以及计算时间的增加。
2.2.配置(CONFIGURATIONS)
作者根据深度的不同列出了从A到E等6种不同的配置(即不同层数的VGG网络结构):
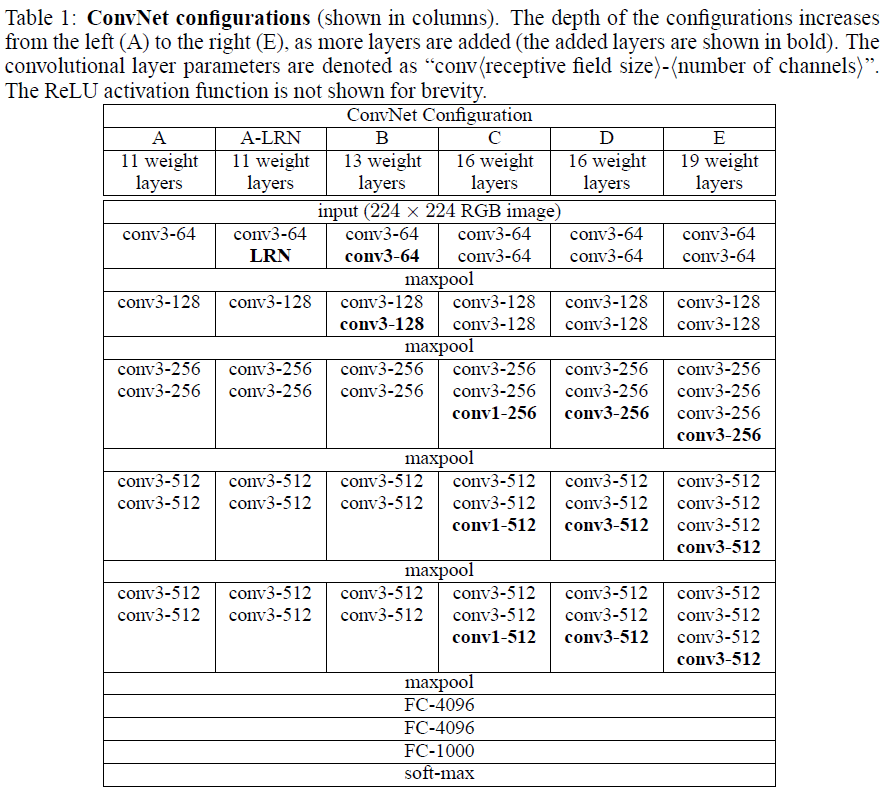
所有的参数设置都遵循2.1部分。卷积核的个数从64开始,每经过一个max-pooling,卷积核的个数就翻倍(乘2)一次。表1中需要注意的一点就是卷积核的表示方法:conv<卷积核大小>-<卷积核个数>,例如conv3-64表示卷积核的大小为3*3,个数为64。
VGG16结构的详细介绍请见本人的另一篇博客:VGG16详细结构。
每种配置的参数数量见下。可以看出,相比于较浅的网络但是使用较大的卷积核的情况,虽然VGG网络的深度很深,但其参数数量并不多。

2.3.讨论(DISCUSSION)
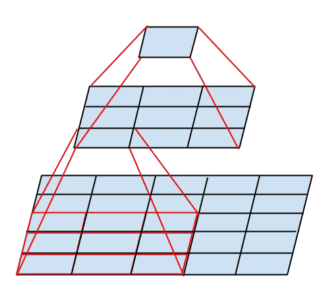
与AlexNet(ILSVRC2012)、ZFNet(ILSVRC2013)、OverFeat(ILSVRC2013)这些已经在ILSVRC2012-2013中取得优异成绩的网络结构相比,VGG并没有在第一个卷积层就使用很大的卷积核(AlexNet在第一个卷积层使用的卷积核大小为$11\times 11$,步长为4;ZFNet和OverFeat在第一个卷积层使用的卷积核大小为$7\times 7$,步长为2)。VGG网络基本全部使用$3\times 3$大小的卷积核,并且步长均为1,并且在输入层之后,可能连续会有多个卷积层的堆叠(中间不再pooling),这样做的效果是(示意图见下):当有两个卷积层堆叠时,第二个卷积层的$3\times 3$感受野映射到输入层就是$5\times 5$;当有三个卷积层堆叠时,第三个卷积层的$3\times 3$感受野映射到输入层就是$7\times 7$。即将大的卷积核拆分成小的卷积核搭配多个堆叠的卷积层。这样做的好处有以下几点:1)多个堆叠的卷积层可以使用多次ReLU激活函数,相比只有一层使用一次ReLU激活函数,前者使得网络对特征的学习能力更强;2)有效的降低了网络参数数量,比如三个堆叠的卷积层搭配$3\times 3$的卷积核的参数数量为$3\times 3\times 3\times C\times C=27C^2$,而一个卷积层搭配$7\times 7$的卷积核的参数数量为$7\times 7\times C\times C=49C^2$(假设输入数据的通道数和卷积核的个数均为$C$)。
此外,VGG配置C还使用了$1\times 1$的卷积核,借鉴自NIN。
GoogLeNet作为ILSVRC-2014的冠军,和VGG类似,也采用了较深的网络结构以及较小的卷积核。
3.分类框架(CLASSIFICATION FRAMEWORK)
在第2部分中,我们详细介绍了VGG的网络配置。在这一部分,我们将着重介绍网络的训练以及评估。
3.1.训练(TRAINING)
网络的训练基本和AlexNet一样,方法也是MBGD+Momentum梯度下降法。mini-batch size=256,momentum系数=0.9。使用L2正则化,其系数设置为$5 \cdot 10^{-4}$。对前两个FC层使用dropout,概率为0.5。学习率初始值设为$10^{-2}$,然后每当验证集的准确率不再提升时,就将学习率缩小10倍。最终,学习率缩小了3次,一共迭代了37万次(74个epoch)。相比AlexNet,尽管VGG的参数更多、深度更深,但是VGG却能更快的收敛,原因在于:1)更小的卷积核以及更大的深度所带来的隐式正则化;2)某些层的预先初始化。
网络权值的初始化是非常重要的。首先训练深度最浅的配置A,对权值进行随机初始化。然后在训练更深的网络配置时,使用配置A的前四个卷积层以及后三个FC层的参数去初始化对应层的权值,中间层的权值依旧采用随机初始化。并且这种预先初始化不会降低其学习率,只有在训练的时候才会调整学习率。在随机初始化权值时,一律采用均值为0,方差为$10^{-2}$的正态分布。偏置项一律初始化为0。需要注意的是,在该论文提交之后,VGG的作者发现还可以使用这篇论文(Glorot, X. and Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proc.AISTATS, volume 9, pp. 249–256, 2010.)的随机初始化方式而不需要再进行预训练的初始化。
VGG的Data Augmentation方式和AlexNet一致,在此不再详述。
VGG网络的输入大小为$224\times 224$,和AlexNet类似,需要先对训练集中的原始图像进行等比例缩放(isotropically-rescaled),将原始训练图像的短边rescale为长度S(长边按照相同的比例缩放),然后再从中提取$224\times 224$的patch。VGG考虑了两种设定S值的方法:
方法一(单尺度训练):将S设置为一个定值,只需满足$S\geqslant 224$即可。VGG作者评估了两个值S=256和S=384。S=256应用比较广泛,AlexNet、ZFNet、OverFeat均使用S=256。在训练S=384的网络时,为了加快训练,使用了S=256时训练得到的网络的权值用于初始化。并且当S=384时,学习率改为$10^{-3}$。
方法二(多尺度训练):S在范围$[S_{min},S_{max}]$内随机取值(VGG作者使用$S_{min}=256,S_{max}=512$)。这样做的好处是考虑到了检测目标在图像中的大小可能是不固定的(有大有小),并且这也可以看做是对训练集的一种Data Augmentation。为了加速训练,使用已经经过单尺度(S=384)训练完的相同配置的网络权值进行初始化。
为了比较单尺度训练和多尺度训练的优劣(即比较不同的S取值),作者需要使用不同的S值训练模型,为了加速其训练过程,作者做了如下措施:1)首先使用S=256训练6种网络配置(先训练配置A,剩余的会用配置A去初始化);2)使用S=384训练6种网络配置,使用第一步得到的网络权值进行对应配置的初始化(为了加快收敛,此时学习率为$10^{-3}$);3)S在[256,512]之间随机取值,然后训练6种网络配置,并且使用第二步得到的网络权值进行对应配置的初始化。
3.2.测试(TESTING)
对测试图像同样先进行等比例缩放,短边rescale为长度Q。Q不一定等于S(并且后续结果证明针对一个S,使用多个不同的Q有助于性能的提升)。从2.2部分的网络结构表中,我们可以看出每种配置都是经历了5次pooling,因此最后一个卷积层的输出大小均为$7\times 7\times 512$,也就是说,无论哪种配置,第一个FC层的输入大小均为$7\times 7\times 512$。我们现在将第一个FC层理解为一个卷积层,卷积核的大小为$7\times 7\times 512$,卷积核的个数为4096,这样我们得到的结果是完全一样的。对剩余的两个FC层进行同样的转换(卷积核大小为$1\times 1\times 4096$),这样我们就将整个网络转换成了全都是卷积层的网络(fully-convolutional net,FCN)。这样做的好处是可以不用对rescale后的测试图像进行裁剪,直接输入该网络,便可得到每个$224\times 224$patch的预测结果(本部分的原理讲解请见本人的另一篇博客:【深度学习基础】第三十三课:基于滑动窗口的目标检测算法)。最后对不同patch预测结果做一个平均(对应通道做平均),这样便得到了一个固定size的预测结果,维度为$1\times 1\times 1000$。此外,作者也对测试图像做了水平翻转,原始测试图像预测结果和对应翻转图像预测结果的平均作为该测试图像的最终预测结果。这种将FC层转换成卷积层,不对rescale后的测试图像进行裁剪的评估方式,作者称其为dense evaluation。
因此,相比AlexNet,VGG无需对rescale后的测试图像进行裁剪,也不需要对每次裁剪后获得的图像进行重新计算,效率大大提升。但是GoogLeNet发现:对图像进行大量的裁剪,(相比dense evaluation)可以更精细的提取到输入图像的特征,有助于准确率的提升(个人理解:相比dense evaluation这种遍历的方式,只取某些位置的裁剪图像更有针对性,能更好的提取目标特征)。作者称这种评估方式为multi-crop evaluation。作者使用了三个不一样的scale(即三个不一样的Q),在得到的图像内取一个$5\times 5$的网格(grid),该网格包含25个像素点。这25个像素点中的每一个点轮流作为待裁剪图像(大小为$224\times 224$)的左上角(或者右上角、中点等都可以),因此一个$5\times 5$的网格可以得到25张裁剪图像。此外,作者还对每幅图像做了翻转。所以,三个不同的scale共产生了$5\times 5\times 2\times 3=150$张图像。multi-crop evaluation不会改变网络结构,即不需要转换成FCN。
dense evaluation和multi-crop evaluation还有一个区别在于padding的填补方式。dense evaluation可以直接用边缘的真实像素值进行填补,而multi-crop evaluation则只能用0进行填补。
3.3.实现细节(IMPLEMENTATION DETAILS)
编程语言为C++,框架为caffe,多GPU训练(4个GPU),GPU型号为NVIDIA Titan Black GPUs,训练一个网络需要2-3周的时间。
4.分类实验(CLASSIFICATION EXPERIMENTS)
这一部分主要是列出了VGG在图像分类任务中的表现。使用的数据集是ILSVRC-2012(ILSVRC 2012–2014的比赛用的都是这个数据集)。这个数据集包含1000个类别,训练集1.3M张图像,验证集50K张图像,测试集100K张图像。依旧使用top-1和top-5错误率作为评判标准。
4.1.单尺度评估(SINGLE SCALE EVALUATION)

当S为定值(S=256或者S=384)时,有Q=S;当S在$[S_{min},S_{max}]$(即[256,512])之间随机取值时,有$Q=0.5\times (S_{min}+S_{max})$。
从Table-3中可以看出,配置A中LRN的应用并没有带来性能的提升,因此在后续配置B-E中,作者便放弃了使用LRN。
其次,随着网络深度的加深,模型的错误率也呈下降趋势。并且,对于相同深度的C和D,$3\times 3$的卷积核表现要比$1\times 1$的好。当深度达到19层时,错误率便饱和了,不再下降了。但是如果数据集变得更大,可能继续加深网络会得到更好的结果。此外,针对配置B,作者还尝试了取消卷积层的堆叠,直接使用$5\times 5$的卷积层(即两个堆叠的$3\times 3$卷积层换成一个$5\times 5$的卷积层),发现top-1错误率提升了7%,这进一步证实了作者的观点:深层网络+较小的卷积核优于浅层网络+较大的卷积核。
最后,还可以看出多尺度训练优于单尺度训练。
单尺度训练和多尺度训练指的是训练时S的不同取值方式;单尺度评估和多尺度评估指的是测试时Q的不同取值方式。
4.2.多尺度评估(MULTI-SCALE EVALUATION)
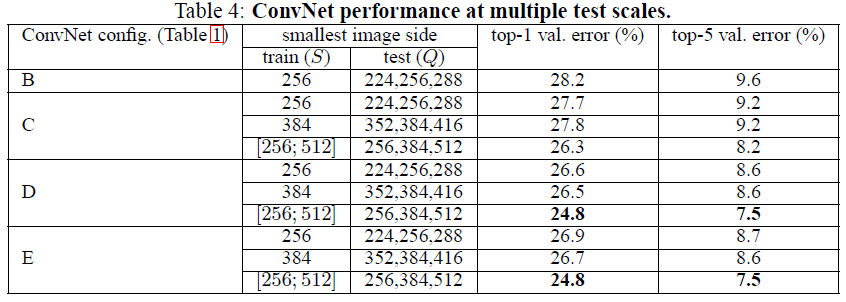
对于固定的S,Q取三个值:S-32、S、S+32;对于随机的S,Q取三个值:$S_{min}$、$0.5\times (S_{min}+S_{max})$、$S_{max}$。最终结果取三个Q值对应结果的平均。
相比单尺度评估,多尺度评估在同一模型上的表现更佳。
4.3.多裁剪评估(MULTI-CROP EVALUATION)
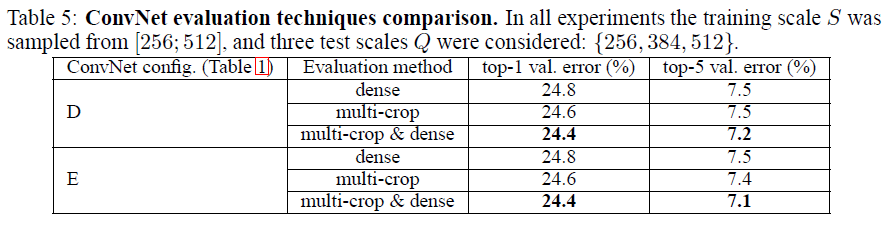
从Table-5中可以看出,multi-crop evaluation比dense evaluation的表现略好。作者还将multi-crop evaluation和dense evaluation的softmax层的输出做了平均,作为multi-crop&dense的结果展示在上表中。可以看到,multi-crop&dense的结果是最好的。作者猜测这是由于两种评估的padding方式不一样而引起的。
4.4.卷积网络融合(CONVNET FUSION)
4.1-4.3部分我们评估的都是单个的卷积神经网络模型。在这一部分中,作者结合了多个模型的输出结果(即取softmax层输出的平均)。结果如下表所示:

作者提交给ILSVRC的结果是7种网络组合得到的预测结果,列在Table6的ILSVRC submission栏位中。其中对于模型(D/[256;512]/256,384,512),作者只是fine-tune了FC层,并没有训练所有的层。在提交了ILSVRC结果之后,作者又尝试了多种组合方式,发现了性能更好的组合。最终,VGG在测试集上的top-5错误率低至6.8%(但是在官方提交的版本中,VGG在测试集上的top-5错误率为7.3%)。
4.5.结果对比(COMPARISON WITH THE STATE OF THE ART)
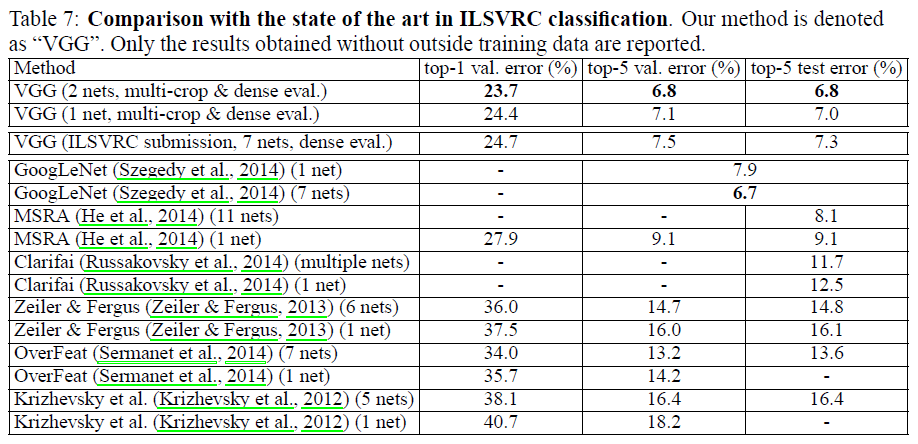
VGG在ILSVRC-2014中以7.3%的测试集top-5错误率取得了分类任务第二名的成绩。GoogLeNet在ILSVRC-2014中以6.7%的测试集top-5错误率取得了分类任务第一名的成绩。
VGG在ILSVRC-2014中以25.3%的错误率取得了定位任务的第一名。
5.结论(CONCLUSION)
VGG证实了增加卷积神经网络的深度有利于提升分类精度。
6.原文链接
👽VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION