本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.原理
实际情况下几乎所有的角点都不会是一个真正的准确像素点,比如$(100,5)$,实际上可能是$(100.234,5.789)$。
亚像素级别的角点检测基于的一个重要条件是:从亚像素点$q$到位于$q$邻域内任意像素点$p$的向量都与$p$处的图像梯度正交:
\[DI_{p_i}^T \cdot (q-p_i) = 0 \tag{1}\]其中,$DI_{p_i}$是像素点$p_i$处的图像梯度:
\[DI_{p_i} = \begin{bmatrix} dx \\ dy \end{bmatrix}, \quad DI_{p_i} ^T= \begin{bmatrix} dx & dy \end{bmatrix}, \quad DI_{p_i} \cdot DI_{p_i} ^T = \begin{bmatrix} dxdx & dxdy \\ dxdy & dydy \\ \end{bmatrix} \tag{2}\]那么式(1)为什么会一直成立呢?我们用下图进行一下解释。
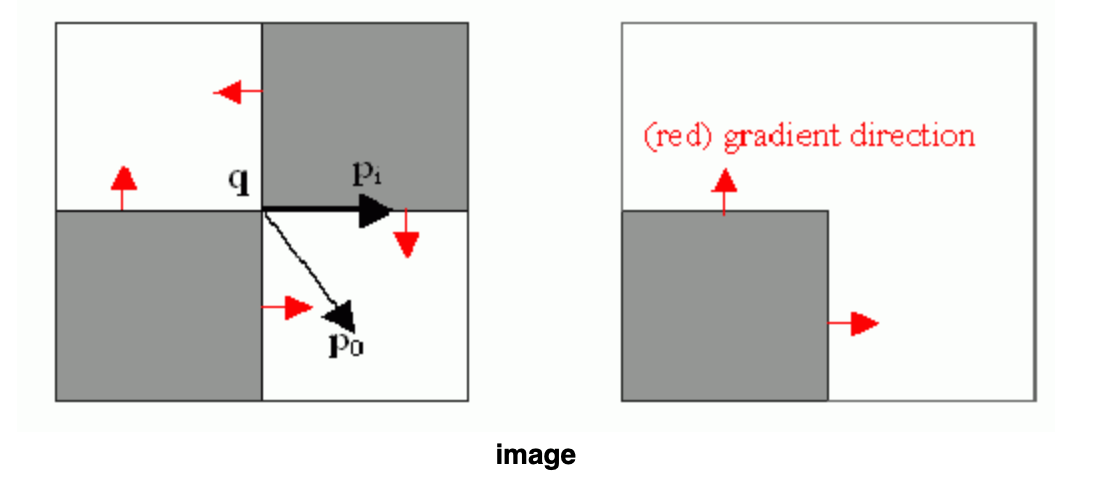
$p_i$的位置我们只考虑两种可能:
- $p_i$位于一片灰度值基本没有变化的区域,即上图中的$p_0$。
- $p_i$位于灰度值变化的边缘,即上图中的$p_1$。
如果是第一种情况:此时$DI_{p_i}$几乎是等于0的,所以式(1)成立。
如果是第二种情况:此时$DI_{p_i}$的方向如上图中红色箭头所示,其和向量$\vec{q p_i}$是正交的,两个正交向量的点积自然是0。
将式(1)移项:
\[DI_{p_i}^T \cdot q = DI_{p_i}^T \cdot p_i \tag{3}\]最小二乘法求解:
\[DI_{p_i} \cdot DI_{p_i}^T \cdot q = DI_{p_i} \cdot DI_{p_i}^T \cdot p_i \tag{4}\]通常$q$点只有一个,但是$p_i$有多个(假设有$N$个),所以式(4)可表示为:
\[\left\{ \begin{array}{c} DI_{p_0} \cdot DI_{p_0}^T \cdot q = DI_{p_0} \cdot DI_{p_0}^T \cdot p_0 \\ DI_{p_1} \cdot DI_{p_1}^T \cdot q = DI_{p_1} \cdot DI_{p_1}^T \cdot p_1 \\ \cdots \\ DI_{p_N} \cdot DI_{p_N}^T \cdot q = DI_{p_N} \cdot DI_{p_N}^T \cdot p_N \end{array} \right. \tag{5}\]把方程组(5)的左右分别加起来:
\[\sum_{i=0}^N ( DI_{p_i} \cdot DI_{p_i}^T) \cdot q =\sum_{i=0}^N ( DI_{p_i} \cdot DI_{p_i}^T \cdot p_i) \tag{6}\]即:
\[q =\left[ \sum_{i=0}^N (DI_{p_i} \cdot DI_{p_i}^T)\right] ^{-1} \cdot \sum_{i=0}^N \left( DI_{p_i} \cdot DI_{p_i}^T \cdot p_i \right) \tag{7}\]此外,由于各个$p_i$点到$q$的距离不一样,我们可以将$p_i$赋予不同的权重:
\[q =\left[ \sum_{i=0}^N (DI_{p_i} \cdot DI_{p_i}^T \cdot w_i)\right] ^{-1} \cdot \sum_{i=0}^N \left( DI_{p_i} \cdot DI_{p_i}^T \cdot p_i \cdot w_i \right) \tag{8}\]2.cv::cornerSubPix
1
2
3
4
5
6
7
void cornerSubPix(
InputArray image,
InputOutputArray corners,
Size winSize,
Size zeroZone,
TermCriteria criteria
);
参数详解:
InputArray image:输入图像,需要为单通道8-bit(比如灰度图像)或float类型图像。InputOutputArray corners:输入为检测到的角点(像素级别),输出为refine后的亚像素级别的角点。Size winSize:用于限定$p_i$的搜索范围。比如,winSize=Size(5,5),则搜索范围为$(5 * 2 +1) \times (5 * 2 +1) = 11 \times 11$。Size zeroZone:见第3部分的解释。TermCriteria criteria:迭代优化的终止条件。可以是以下两种条件其一或者二者兼有:TermCriteria::MAX_ITER:最大迭代次数。TermCriteria::EPS:最小误差。
3.源码解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
void cv::cornerSubPix( InputArray _image, InputOutputArray _corners,
Size win, Size zeroZone, TermCriteria criteria )
{
CV_INSTRUMENT_REGION();
const int MAX_ITERS = 100;
int win_w = win.width * 2 + 1, win_h = win.height * 2 + 1;
int i, j, k;
int max_iters = (criteria.type & CV_TERMCRIT_ITER) ? MIN(MAX(criteria.maxCount, 1), MAX_ITERS) : MAX_ITERS;
double eps = (criteria.type & CV_TERMCRIT_EPS) ? MAX(criteria.epsilon, 0.) : 0;
eps *= eps; // use square of error in comparison operations
cv::Mat src = _image.getMat(), cornersmat = _corners.getMat();
int count = cornersmat.checkVector(2, CV_32F);
CV_Assert( count >= 0 );
Point2f* corners = cornersmat.ptr<Point2f>();
if( count == 0 )
return;
CV_Assert( win.width > 0 && win.height > 0 );
CV_Assert( src.cols >= win.width*2 + 5 && src.rows >= win.height*2 + 5 );
CV_Assert( src.channels() == 1 );
Mat maskm(win_h, win_w, CV_32F), subpix_buf(win_h+2, win_w+2, CV_32F);
float* mask = maskm.ptr<float>();
for( i = 0; i < win_h; i++ )
{
float y = (float)(i - win.height)/win.height;
float vy = std::exp(-y*y);
for( j = 0; j < win_w; j++ )
{
float x = (float)(j - win.width)/win.width;
mask[i * win_w + j] = (float)(vy*std::exp(-x*x));
}
}
// make zero_zone
if( zeroZone.width >= 0 && zeroZone.height >= 0 &&
zeroZone.width * 2 + 1 < win_w && zeroZone.height * 2 + 1 < win_h )
{
for( i = win.height - zeroZone.height; i <= win.height + zeroZone.height; i++ )
{
for( j = win.width - zeroZone.width; j <= win.width + zeroZone.width; j++ )
{
mask[i * win_w + j] = 0;
}
}
}
// do optimization loop for all the points
for( int pt_i = 0; pt_i < count; pt_i++ )
{
Point2f cT = corners[pt_i], cI = cT;
int iter = 0;
double err = 0;
do
{
Point2f cI2;
double a = 0, b = 0, c = 0, bb1 = 0, bb2 = 0;
getRectSubPix(src, Size(win_w+2, win_h+2), cI, subpix_buf, subpix_buf.type());
const float* subpix = &subpix_buf.at<float>(1,1);
// process gradient
for( i = 0, k = 0; i < win_h; i++, subpix += win_w + 2 )
{
double py = i - win.height;
for( j = 0; j < win_w; j++, k++ )
{
double m = mask[k];
double tgx = subpix[j+1] - subpix[j-1];
double tgy = subpix[j+win_w+2] - subpix[j-win_w-2];
double gxx = tgx * tgx * m;
double gxy = tgx * tgy * m;
double gyy = tgy * tgy * m;
double px = j - win.width;
a += gxx;
b += gxy;
c += gyy;
bb1 += gxx * px + gxy * py;
bb2 += gxy * px + gyy * py;
}
}
double det=a*c-b*b;
if( fabs( det ) <= DBL_EPSILON*DBL_EPSILON )
break;
// 2x2 matrix inversion
double scale=1.0/det;
cI2.x = (float)(cI.x + c*scale*bb1 - b*scale*bb2);
cI2.y = (float)(cI.y - b*scale*bb1 + a*scale*bb2);
err = (cI2.x - cI.x) * (cI2.x - cI.x) + (cI2.y - cI.y) * (cI2.y - cI.y);
cI = cI2;
if( cI.x < 0 || cI.x >= src.cols || cI.y < 0 || cI.y >= src.rows )
break;
}
while( ++iter < max_iters && err > eps );
// if new point is too far from initial, it means poor convergence.
// leave initial point as the result
if( fabs( cI.x - cT.x ) > win.width || fabs( cI.y - cT.y ) > win.height )
cI = cT;
corners[pt_i] = cI;
}
}
👉第一步:读入传进来的参数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
CV_INSTRUMENT_REGION();
const int MAX_ITERS = 100;
int win_w = win.width * 2 + 1, win_h = win.height * 2 + 1;
int i, j, k;
int max_iters = (criteria.type & CV_TERMCRIT_ITER) ? MIN(MAX(criteria.maxCount, 1), MAX_ITERS) : MAX_ITERS;
double eps = (criteria.type & CV_TERMCRIT_EPS) ? MAX(criteria.epsilon, 0.) : 0;
eps *= eps; // use square of error in comparison operations
cv::Mat src = _image.getMat(), cornersmat = _corners.getMat();
int count = cornersmat.checkVector(2, CV_32F);
CV_Assert( count >= 0 );
Point2f* corners = cornersmat.ptr<Point2f>();
if( count == 0 )
return;
CV_Assert( win.width > 0 && win.height > 0 );
CV_Assert( src.cols >= win.width*2 + 5 && src.rows >= win.height*2 + 5 );
CV_Assert( src.channels() == 1 );
这里需要注意的是传进来的最小误差eps做了一个平方的处理,所以实际用的误差阈值是eps*eps。
👉第二步:生成权重矩阵。这里使用的是高斯分布。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Mat maskm(win_h, win_w, CV_32F), subpix_buf(win_h+2, win_w+2, CV_32F);
float* mask = maskm.ptr<float>();
for( i = 0; i < win_h; i++ )
{
float y = (float)(i - win.height)/win.height;
float vy = std::exp(-y*y);
for( j = 0; j < win_w; j++ )
{
float x = (float)(j - win.width)/win.width;
mask[i * win_w + j] = (float)(vy*std::exp(-x*x));
}
}
// make zero_zone
if( zeroZone.width >= 0 && zeroZone.height >= 0 &&
zeroZone.width * 2 + 1 < win_w && zeroZone.height * 2 + 1 < win_h )
{
for( i = win.height - zeroZone.height; i <= win.height + zeroZone.height; i++ )
{
for( j = win.width - zeroZone.width; j <= win.width + zeroZone.width; j++ )
{
mask[i * win_w + j] = 0;
}
}
}
假设我们传进来的winSize=Size(5,5),那实际搜索窗口大小为$11 \times 11$,生成的高斯分布权重矩阵见下(越靠近中心点,权重越大,中心点权重为1):
1
2
3
4
5
6
7
8
9
10
11
0.135335 0.19398 0.256661 0.313486 0.353455 0.367879 0.353455 0.313486 0.256661 0.19398 0.135335
0.19398 0.278037 0.367879 0.449329 0.506617 0.527292 0.506617 0.449329 0.367879 0.278037 0.19398
0.256661 0.367879 0.486752 0.594521 0.67032 0.697676 0.67032 0.594521 0.486752 0.367879 0.256661
0.313486 0.449329 0.594521 0.726149 0.818731 0.852144 0.818731 0.726149 0.594521 0.449329 0.313486
0.353455 0.506617 0.67032 0.818731 0.923116 0.960789 0.923116 0.818731 0.67032 0.506617 0.353455
0.367879 0.527292 0.697676 0.852144 0.960789 1 0.960789 0.852144 0.697676 0.527292 0.367879
0.353455 0.506617 0.67032 0.818731 0.923116 0.960789 0.923116 0.818731 0.67032 0.506617 0.353455
0.313486 0.449329 0.594521 0.726149 0.818731 0.852144 0.818731 0.726149 0.594521 0.449329 0.313486
0.256661 0.367879 0.486752 0.594521 0.67032 0.697676 0.67032 0.594521 0.486752 0.367879 0.256661
0.19398 0.278037 0.367879 0.449329 0.506617 0.527292 0.506617 0.449329 0.367879 0.278037 0.19398
0.135335 0.19398 0.256661 0.313486 0.353455 0.367879 0.353455 0.313486 0.256661 0.19398 0.135335
这里用的生成高斯分布权重矩阵的公式为:
\[e^{-\left[ \left( \frac{x-\mu_x}{\mu_x} \right)^2 + \left( \frac{y-\mu_y}{\mu_y} \right)^2 \right] }\]如果我们传进来的winSize=Size(5,5),那就有$\mu_x = \mu_y = 5, \ x\in [0,10], \ y\in [0,10]$。
而传进来的参数zeroZone用于屏蔽掉某些位置上的权重,做法是将该位置的权重置为0,即计算时不考虑这些位置上的像素点$p_i$。zeroZone也是以搜索窗口的中心为中心的。如果zeroZone=Size(-1,-1),则搜索窗口内的所有点都不会被屏蔽。
👉第三步:计算亚像素角点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
// do optimization loop for all the points
for( int pt_i = 0; pt_i < count; pt_i++ )
{
Point2f cT = corners[pt_i], cI = cT;
int iter = 0;
double err = 0;
do
{
Point2f cI2;
double a = 0, b = 0, c = 0, bb1 = 0, bb2 = 0;
getRectSubPix(src, Size(win_w+2, win_h+2), cI, subpix_buf, subpix_buf.type());
const float* subpix = &subpix_buf.at<float>(1,1);
// process gradient
for( i = 0, k = 0; i < win_h; i++, subpix += win_w + 2 )
{
double py = i - win.height;
for( j = 0; j < win_w; j++, k++ )
{
double m = mask[k];
double tgx = subpix[j+1] - subpix[j-1];
double tgy = subpix[j+win_w+2] - subpix[j-win_w-2];
double gxx = tgx * tgx * m;
double gxy = tgx * tgy * m;
double gyy = tgy * tgy * m;
double px = j - win.width;
a += gxx;
b += gxy;
c += gyy;
bb1 += gxx * px + gxy * py;
bb2 += gxy * px + gyy * py;
}
}
double det=a*c-b*b;
if( fabs( det ) <= DBL_EPSILON*DBL_EPSILON )
break;
// 2x2 matrix inversion
double scale=1.0/det;
cI2.x = (float)(cI.x + c*scale*bb1 - b*scale*bb2);
cI2.y = (float)(cI.y - b*scale*bb1 + a*scale*bb2);
err = (cI2.x - cI.x) * (cI2.x - cI.x) + (cI2.y - cI.y) * (cI2.y - cI.y);
cI = cI2;
if( cI.x < 0 || cI.x >= src.cols || cI.y < 0 || cI.y >= src.rows )
break;
}
while( ++iter < max_iters && err > eps );
// if new point is too far from initial, it means poor convergence.
// leave initial point as the result
if( fabs( cI.x - cT.x ) > win.width || fabs( cI.y - cT.y ) > win.height )
cI = cT;
corners[pt_i] = cI;
}
最外层的for循环用于遍历每一个角点。内层的do循环用于对某一角点进行refine。重点就是这个do循环。首先以某一角点为中心截取搜索窗口,这里$p_i$的横纵坐标分别用px和py表示(都是相对于窗口中心的相对坐标),这里采用式(8)的计算,先来看式(8)的前半部分,其中
\[DI_{p_i} \cdot DI_{p_i}^T \cdot w_i\]用代码里的符号表示就是:
\[\begin{bmatrix} gxx & gxy \\ gxy & gyy \end{bmatrix}\]加上求和之后
\[\sum_{i=0}^N (DI_{p_i} \cdot DI_{p_i}^T \cdot w_i)\]用代码里的符号表示就是:
\[\begin{bmatrix} \sum gxx & \sum gxy \\ \sum gxy & \sum gyy \end{bmatrix} = \begin{bmatrix} a & b \\ b & c \end{bmatrix}\]式(8)的后半部分
\[DI_{p_i} \cdot DI_{p_i}^T \cdot p_i \cdot w_i\]用代码里的符号表示就是:
\[\begin{bmatrix} gxx & gxy \\ gxy & gyy \end{bmatrix} \begin{bmatrix} px \\ py \end{bmatrix} = \begin{bmatrix} gxx * px + gxy * py \\ gxy * px + gyy * py \end{bmatrix}\]加上求和之后
\[\sum_{i=0}^N \left( DI_{p_i} \cdot DI_{p_i}^T \cdot p_i \cdot w_i \right)\]用代码里的符号表示就是:
\[\begin{bmatrix} \sum (gxx * px + gxy * py) \\ \sum (gxy * px + gyy * py) \end{bmatrix} = \begin{bmatrix} bb1 \\ bb2 \end{bmatrix}\]然后对于式(8)的前半部分,我们还需要求其逆矩阵,$2\times 2$矩阵的逆矩阵的计算见下:
\[A^{-1} = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{bmatrix}^{-1} = \frac{1}{A_{11}A_{22} - A_{12}A_{21}} \begin{bmatrix} A_{22} & -A_{12} \\ -A_{21} & A_{11} \\ \end{bmatrix}\]那么用代码里的符号表示就是:
\[\begin{bmatrix} a & b \\ b & c \end{bmatrix}^{-1} = \frac{1}{a*c-b*b} \begin{bmatrix} c & -b \\ -b & a \end{bmatrix} = \frac{1}{\text{det}} \begin{bmatrix} c & -b \\ -b & a \end{bmatrix} = \text{scale} \begin{bmatrix} c & -b \\ -b & a \end{bmatrix}\]所以式(8)最终完整可表示为:
\[\text{scale} \begin{bmatrix} c & -b \\ -b & a \end{bmatrix} \cdot \begin{bmatrix} bb1 \\ bb2 \\ \end{bmatrix} = \begin{bmatrix} c*\text{scale}*bb1 - b*\text{scale}*bb2 \\ - b*\text{scale}*bb1 + a*\text{scale}*bb2 \\ \end{bmatrix}\]因为px,py是相对坐标,所以需要再加上原始角点(即代码中的$\text{cI}$)的绝对坐标,最终得到refine后的亚像素坐标(即代码中的$\text{cI2}$)。
这里do循环的跳出条件有两个,一个是迭代次数满足预设的最大次数,这里每refine一个角点就算是一次迭代,所以这里的迭代次数指的就是需要refine的角点的个数。另一个条件是误差小于阈值,误差的计算见下:
\[\text{err} = (\text{cI2}.x - \text{cI.x})^2 +(\text{cI2}.y - \text{cI.y})^2\]即得到的亚像素角点基本已经收敛,几乎不再变化了。